|
|
© 2004 Tonalsoft Inc. |
|
|
© 2004 Tonalsoft Inc. |
TABLE OF CONTENTS
AN EQUAL-TEMPERED UNIT OF MEASUREMENT: THE SEMITONE
I have independently developed a theory almost identical in concept to
Ben Johnstonís, but with some important differences in the notational
system. The objections I have to Johnstonís notation were neatly summarized
recently in 1/1 by Daniel J. Wolf, whose notation, although
it uses different symbols, accepts as a solution the same structural
layout as my JustMusic notation.
AN EQUAL-TEMPERED UNIT OF MEASUREMENT:
THE SEMITONE
2 is the proportion which represents the "octave",
so what we perceive
as being linearly 1/12 of this - or the JustMusic
Semitone
- is an irrational proportion:
1 : 1 : 2(1/12) =
approx. 1 : 1.0594631 =
100 cents =
1.00 Semitone
(1)
![]() =
=
This is the basic measurement used in the standard 12-EQ scale: each degree is 1.00 Semitone apart, and it is very useful for comparing just-intonation intervals and relating them to our familiar scale.
A LOGICAL MATRIX-BASED NOTATION
Ratios Notated As A Prime Series
A ratio may be written and manipulated as a fraction, and each of its terms may be factored according to the Fundamental Theorem of Arithmetic into a series which consists of the series of positive prime integers, each of which is considered as a base raised to zero or positive integer exponents; these are then multiplied together to arrive at the product which expresses a term in the proportional number
Since
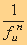
| = | 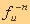
| (2) |
the fraction can be eliminated, and the series of prime-bases raised to zero, positive, and negative integers can be used. This was stated succinctly by Douglas Keislar:
Any just interval is expressible as the product of powers of prime numbers:
| 2a * 3b * 5c * Ln | (3) |
where a thru n are integers,
and L, called the "limit" of the system, is the largest prime number in the series.
For example:
2-1 31 50 70... = 1/2 * 3 * 1 * 1... = 3/2 (This is a 3-Limit ratio)
The fundamental unit is the octave, which has the unique property that its two notes are felt in some indefinable way to be the same, though in pitch level they are recognizably different.
Any frequency f
compared to itself is expressed as the unity ratio:
(for example: 256 Hz : 256 Hz = 1 : 1).
Any frequency f
multiplied by any integer power of 2 results in a musical pitch
which has the same aesthetic properties as
f :
where p
In current terminology, this is called "octave equivalence".
Eliminating the "octaves": Pitch-class
For any integer x,
since x * 1 =
x,
and x0
= 1 and, from equation (2),
2x
Besides its elegance, another advantage of this notation is that
it discloses important information about:
JustMusic is based on the set of prime integers
{3, 5, 7, 11, 13, 17, 19} as bases of the ratio terms. This arbitrary
upper limit on the set of prime integer bases is referred to as the
19-Limit (analagous to Partch's terminology of odd
limits). Whether
referring to a tone, scale, composition, or entire musical system,
the prime-limit is indicated by the highest prime base which
has a non-zero exponent.
To simplify notation, the bases may be omitted, and the exponents
alone presented as a series, in which case zero-exponents must be
included as place-holders:
where {a,...g} and
a = 3a,
b = 5b,
c = 7c,
d = 11d,
e = 13e,
f = 17f,
and g = 19g
For example:
9 9 Therefore, 2 -1 0 0 -1 0 0 º 72/65
(This particular ratio falls within the 13-Limit.) The representational procedure used by this notation is somewhat
analogous to that used in our standard mathematical numbering system.
Here, the least significant digit (the exponent of prime-base 3) is
on the left. By assuming the series of prime-bases as a given, and
notating only the exponents, the two important parameters of frequency
relationship, namely sonance and tonal proximity, are obviously exposed
by indicating the prime-bases involved and by the "weight" of each prime
as revealed by the absolute value of its exponent.
This notational scheme also forms the basis for JustMusic
mathematical operations, such as calculating intervals (see below).
I believe that sophisticated systemic mathematical procedures can be
applied to the exponents in the prime series in ways similar to those
applied by contemporary composers and theorists to the set of integers
{0,...11} which represent pitch-classes of the 12-EQ system.
In addition, this notational scheme is exactly analogous to the
JustMusic Planetary Graph, described in my book.
Because this notational system can be used with any combination
of prime-bases, I usually find it less cumbersome to use the bases
as well as the exponents in the notation, thus omitting primes which
have a zero exponent (primes which are º 1).
These series of bases-and-exponents, along with naturals, sharps, flats,
and double-sharps and double-flats, constitute the accidentals which are
printed just before each note in the JustMusic notation.
The seven pitch-classes of the 3-Limit Diatonic minor scale are the
only notes in the system which never need an accidental; for 3-Limit
pitch-classes with sharps and flats, which use only prime-bases
2 and 3, the numerical part of the accidental can be omitted if desired,
because the basic letter-name and sharp/flat parts of JustMusic
notation are based on a 3-limit cycle, exactly as the notation evolved
historically in music theory. Also, to portray the special place of 1/1
as a reference, I use n0
as its accidental.
Calculating Intervals
[As was stated earlier, our perception of adding and
subtracting pitches must be calculated with ratios as multiplication
and division; therefore, I will use quotes around "+" and "-" when
discussing the same.]
There are 2 methods for calculating rational intervals:
multiplication of fractions, and vector addition of exponents.
To add or subtract intervals by vector addition of exponents,
simply add or subtract by vector addition the set of exponents
for each tone or interval, using 0 where necessary as a placeholder:
Examples:
"Major Third + Minor Third" =
51 (= 5/4) * 315-1 (= 6/5) =
"Perfect Fifth - Major Third" =
31 (= 3/2) ¸ 51 (= 5/4) =
And as always, two negatives make a positive:
"Major Third - Perfect Fourth" =
51 (= 5/4) ¸ 3-1 (= 4/3) =
BUILDING THE MATRIX
It is my belief (extrapolating on Partch's observations) that musicians
have adopted the use of each successive higher prime gradually throughout
musical history. In my book, I show how standard letter-name notation
with sharps and flats arose within a 3-Limit (or Pythagorean)
tuning system.
The historical outline in my book is presented with an admitted bias
toward Western theory; however, I do believe that my ideas can be applied
with great success to the musical systems of other cultures. This could
correct the mistake that has occurred of forcing non-Western music into
the mold of our familiar system simply because it was the best way that
could be found to represent these unfamiliar musics to Western readers.
I explore the ancient Greek and Indian scale systems for just this reason,
since they have little bearing on modern European music-theory.
In JustMusic notation, the powers of 3 which are factors
in the ratio can be represented by the usual letters and note-heads,
accompanied when necessary by the standard sharp/flat accidentals. As
each following prime number is introduced, it must be indicated along
with its exponent, as part of the accidental. (Simply for the sake of
completeness, I generally indicate prime-base 3 also.)
Starting Point: A Reference Tone
The approximate range of human hearing is from 20 to 20,000 Hz.
Described as powers of 2, this is roughly 24 (=16) to
214 (= 16,384) Hz.
Since 2n
º 1, and since 28 Hz= 256 Hz -
which is quite close to "middle-C" in the standard 12-EQ scale based
on A-440 Hz - the basic reference tone which I use is
n0 = C-1 Hz.
Since my whole system is based on proportional numerical measurement,
I feel this is the most logical starting point.
Alternatively, "middle-C" may be equated with
n0,
with lower "octaves" descending through the negative exponents of 2,
and higher "octaves" ascending through the positive exponents.
Thus, the exponents of prime-base 2 will indicate the beginning
of each new ascending "octave", represented in notation as follows:
[note from November 2003: as of now, i have quite decisively come
to prefer the version with "middle-C" as
n0.
If 256 Hz ( 28 Hz) is retained as "middle-C" in the version where "middle-C' is
n0,
then 1 Hz would be equated to 2 -7. The graph shows
that that at the low end of the audible range, 16 (= 24) Hz
is equated to 2 -4. At the high end, 214 (= 16,384) Hz
would be equated to 26.
Another benefit of "middle-C" centricity is that the historically
important pitches of treble-G and bass-F, which are the references
for their respective clefs and whose letters actually became
transformed into those clefs, are exactly a
"perfect-5th"
above and below "middle-C" respectively.]
The first dimension: prime-base 3
Starting with the first prime base in the series which is not
equivalent to unity, namely 3, we can build a scale of musical
materials by using exponents which increase and decrease from 0,
and by multiplying one of the terms continuously by 2 until the
ratio falls between 1 and 2, as follows:
30 = 1 = 1/1 31 = 3 = 3/1, . . . 3-1 = 1/3, . . . On a graph, the x-axis will represent the integer exponents of prime base 3,
and letter-names and Semitone values are supplied along with the ratios:
4 D 4.98 1 A 0.00 3 E 7.02 3-1
n0
31
The prime-factor notation represents
these pitch-classes in all their "octaves", with the regular staff notation
displaying the "octave" registration.
The tonal relationships of 3-1 : 30 and
31 : 30 will be recognized by musicians as the
important ones of "subdominant" and "dominant" respectively.
The Pythagorean Diatonic (minor) scale.
All ancient Pythagorean accounts of the diatonic genus of the Greek
system are given thus:
This scale was easily tuned by ear by means of a series
of the "Perfect 4ths" [= 3-1] and "Perfect 5ths"
[= 31] outlined above.
Arranged into table whose x-axis represents powers of 3,
and giving letter-names and Semitone values, we get:
ParHypate
Trite Lichanos
ParaNete MESE
Nete Hypate
ParaMese
128 F 7.92 32 C 2.94 16 G 9.96 4 D 4.98 1 A 0.00 3 E 7.02 9 B 2.04 3-4 3-3 3-2 3-1 n0 31 32
If the pitch-classes are given letter-names and rearranged to
fit within the "octave" A to A, it forms what became the standard
Pythagorean diatonic "natural minor" scale, which was briefly described above:
This is the collection of pitch-classes which became the basis of music
theory in ancient Greece, and it was transmitted from the Greek literature
to medieval Europe by Boethius around 500. His theory became
the standard in Europe for about 1000 years.
Most of the standard terminology of harmony derives from this scale:
each pitch-class is assigned an integer degree-number starting from 1,
and intervals are calculated simply by counting degree-integers
inclusively (note that this meaning of "degree" is slightly different,
and less precise, than that previously defined in the EQ equations:
in this scale "degree" does not imply equal steps).
By allowing each of the seven degrees in the standard scale to be
used as either mi or fa in the musica recta system,
auxilliary degrees are obtained which are higher or lower in pitch than
their namesake tone. These are indicated with the use of "accidental" signs,
resulting in a gamut of 17 tones as determined by Prosdocimus:
32768 Gb 8.82 8192 Db 3.84 4096 Ab 10.86 1024 Eb 5.88 256 Bb 0.90 128 F 7.92 32 C 2.94 16 G 9.96 4 D 4.98 1 A 0.00 3 E 7.02 9 B 2.04 27 F# 9.06 81 C# 4.08 243 G# 11.10 729 D# 6.12 2187 A# 1.14 3-9 3-8 3-7 3-6 3-5 3-4 3-3 3-2 3-1 n0 31 32 33 34 35 36 37
The same process can be followed with prime-base 5: 51
5 C# 51 3.86 50
1 A n0 0.00 5-1 8 F 5-1 8.14 30
Ratios which include prime-base 5 as a factor were first used
as more consonant "corrections" for 3-Limit ratios which
are nearby in frequency. Originally, the reconfiguration ran thus:
5y 0 128 F 3-4
7.92
32 C 3-3
2.94
16 G 3-2
9.96 4 D 3-1
4.98
1 A n0
0.00 3 E 31
7.02 9 B 32
2.04 -4
-3
-2
-1
0
1
2
3x Became:
5y
0
4 D 3-1
4.98 1 A n0
0.00 3 E 31
7.02 9 B 32
2.04 -1 8 F 5-1
8.14 6 C 315-1
3.16 9 G 325-1
10.18 -4
-3
-2
-1
0
1
2
3x 5y 0 1 A n0
0.00 3 E 31
7.02 9 B 32
2.04 -1
8 F 5-1
8.14 6 C 315-1
3.16 9 G 325-1
10.18 27 D 335-1
5.20 -4
-3
-2
-1
0
1
2
3
3x Although making "C" the central reference of the whole system [n0]
changes all of the numerical values, both ratios and Semitones, the relationships
between all tones remain exactly the same:
5y
1
5 A
3-151
8.84 5 E 51
3.86 15 B 3151
10.88 0 4 F 3-1
4.98 1 C n0
0.00 3 G 31
7.02 9 D 32
2.04 -5
-4
-3
-2
-1
0
1
2
3x Because of the strong feeling of tonality
inherent in this collection of pitch-classes, the "C-major" scale
in the above graph became the standard reference scale and "key"
of common-practice music in Europe. It is also the basis of Ben Johnstonís
notation, which is my chief criticism of his notational system.
I agree with Wolf that it is better to use a system which is based on the
3-Limit, with each higher prime-base adding its own unique symbol to the
accidental. In my case, the symbols are nothing more than the prime-base
with its appropriate exponent.
While normally actually using such tuning systems as
12-EQ,
meantone,
or well temperaments,
"standard" Eurocentric music theory is based mostly on a
5-Limit just-intonation
conception of harmony.
In practice, musicians often use or imply ratios
with higher prime factors. Theorists have also specified much higher
primes in their descriptions of tuning systems. In order to portray
these systems visually, I have abandoned the matrix format presented here
and instead now use Lattice Diagrams,
which give the ability to represent
any number of prime factors, each with their own unique dimension in
the diagram.
Examples of this approach can be found in the other papers published
on this website.
1998 June 13
References
Wolf, Daniel. 1996. Letter in 1/1, the journal of
the Just-Intonation Network, 9:3 [Summer], p 15.
Babbitt, Milton. 1960. Twelve-Tone Invariants as Compositional Determinants
Barker, Andrew, ed. 1989. Greek Musical Writings, volume 2: Harmonic and Acoustic Theory.
Boretz, Benjamin and Cone, Edward T., ed. 1972. Perspectives on Contemporary Music Theory.
Clynes, Manfred, ed. 1982. Music, Mind, and Brain: the Neuropsychology of Music.
Encyclopaedia Britannica. 1981. Music article. Fonville, John. 1991. Ben Johnston's Extended Just Intonation: A Guide for Interpreters.
Helmholtz, Hermann. [1863] 1954. On the Sensations of Tone
Johnston, Ben. 1964. Scalar Order as a Compositional Resource.
Keislar, Douglas. 1987. The History and Principles of Microtonal Keyboards.
Kraehenbuehl, David and Schmidt, Christopher. 1962. On the Development of Musical Systems.
Monzo, Joseph L. 1997. JustMusic: A New Harmony - Representing Pitch as Prime Series.
updates:
![]()
=
![]()
(4)
2p * f
![]() f
f
(5)
![]() {...-1, 0, 1,...}
{...-1, 0, 1,...}![]() 1, any expression equivalent
to 1 may be omitted from the notation, and only prime integers greater
than 2 and with a non-zero exponent need be used as bases.
1, any expression equivalent
to 1 may be omitted from the notation, and only prime integers greater
than 2 and with a non-zero exponent need be used as bases.
a b c d e f g (6)
![]() {...-1, 0, 1,...}
{...-1, 0, 1,...}
2 -1 0 0 -1 0 0
= 32 5-1 70 110 13-1
170 190
= 9 1
--
51 1 1
---
131 1
=
------
5 * 13
=
---
65* 23 = 72
---
65
Vector Addition actual calculation
[ 0 1] 30 51
+ [ 1 -1] + 31 5-1
_________ = ________
[ 1 0] 31 50 = 31 (= 3/2)
Vector Addition actual calculation
[ 1 0] 31 50
- [ 0 1] - 30 51
_________ = ________
[ 1 -1] 31 5-1 (= 6/5)
Vector Addition actual calculation
[ 0 1] 30 51
- [-1 0] - 3-1 50
_________ = ________
[ 1 1] 31 51 (= 15/8)

![]() *
* ![]() =
= ![]() thus 31 º 3/2
thus 31 º 3/2![]() *
* ![]() =
= ![]() thus 3-1 º 4/3
thus 3-1 º 4/3
--
3
--
1
--
2
ratio Semitones note name
31 7.02 Nete diezeugmenon
3-1 4.98 ParaNete diezeugmenon
3-3 2.94 Trite diezeugmenon
32 2.04 ParaMese
n0 0.00 MESE
3-2 9.96 Lichanos
3-4 7.92 ParHypate
31 7.02 Hypate
diezeugmenon
diezeugmenon
diezeugmenon
--
81
--
27
--
9
--
3
--
1
--
2
--
8
(A n0 0.00)
G 3-2 9.96
F 3-4 7.92
E 31 7.02
D 3-1 4.98
C 3-3 2.94
B 32 2.04
A n0 0.00
-----
19683
----
6561
----
2187
----
729
---
243
---
81
--
27
--
9
--
3
--
1
--
2
--
8
--
16
--
64
---
128
---
512
----
2048
(A n0 12.00)
G# 35 11.10
Ab 3-7 10.86
G 3-2 9.96
F# 3-1 9.06
Gb 3-9 8.82
F 3-4 7.92
E 31 7.02
D# 36 6.12
Eb 3-6 5.88
D 3-1 4.98
C# 34 4.08
Db 3-8 3.84
C 3-3 2.94
B 32 2.04
A# 37 1.14
Bb 3-5 0.90
A n0 0.00
--
4
--
1
--
5
----
81
----
27
----
9
---
3
---
1
---
2
---
8
---
3
---
1
---
2
---
8
---
5
---
5
---
5
Later, as the development of harmony emphasized the juxtaposition of
the "major" [otonal]
and "minor" [utonal] modes, to the
exclusion of all the rest of the old modes,
"D" shifted to 335-1, to give a 4:5:6 triad
on G 325-1, the "Dominant" (V):
---
1
---
2
---
8
---
5
---
5
---
5
----
20
---
3
---
4
---
8
---
3
---
1
---
2
----
8
revised 1998 November 4
and 1998 November 21
The Musical Quarterly, vol 46, p 246-259.
Cambridge University Press, Cambridge.
W. W. Norton & Co., New York.
Plenum Press, New York.
Perspectives of New Music, vol 29, no 2 [Summer], p 106-137.
Trans., Alexander Ellis. Reprint ed., Dover, New York.
Perspectives of New Music, vol 2, no 2 [Spring-Summer], p 56-76.
Computer Music Journal, vol 11, no 1 [Spring], p 18-28.
Journal of Music Theory, vol 6, p 32-65.
(forthcoming).
2002.10.24
2003.11.19 -- "note from November 2003" added in the section
"Starting Point: A Reference Tone"