|
|
© 2004 Tonalsoft Inc. |
|
|
© 2004 Tonalsoft Inc. |
© 1997, 2004 by Joseph L. Monzo
From: monz
> From: Paul Erlich
(Those who have trouble following the Greek terminology here
may get some help from my
"Tutorial on ancient Greek Tetrachord-theory".
In my unpublished paper "An Examination of a Possible 5-Limit System
of Boethius" (1997), the conclusion of which appears in my book
JustMusic: A New Harmony,
I examine the Greek-letter notation
used by Boethius to describe the modes.
There, I assume that the ratios described by Didymus are used for
the diatonic genus, and construct a lattice incorporating all of
the pitches which occur in the complete set of all the modes.
I note how pitches which are separated by a syntonic comma always
have different symbols, but those separated by a skhisma always
have the same symbols.
Boethius's actual theoretical tuning of the diatonic genus supposedly
would have been entirely Pythagorean (3-limit), but as Nicomachus
wrote, c. 100 AD:
>> [Barker 1989, p. 265]
And this distinction is indicated in Boethius's Greek-letter notation.
Much later (c. 900 AD), Hucbald directly contradicted this:
>> [Babb 1978, p 33]
which shows that the basic diatonic tuning had changed by his time.
The only tuning system which would have been a good candidate for
Boethius's time which gives pitches matching his descriptions and
notations, is that of Didymus (c. 50 BC - 100 AD), where the
protypical tetrachord is [descending]:
Boethius's description and diagrams of the modal system are
in his Book 4, chapters 16 and 17 [Bower 1989, p 154-160].
A link to the Latin text is given below.
Constructing lattices for
each mode notated by Boethius,
but according to the tuning of Didymus, results
in a general lattice for the whole system, with pairs
of pitches which are
separated by a skhisma
(~2 cents) but notated
with the same letter, one of them occuring with the pair 3^3
(= 27:16 = ~906 cents) and 3^-5 * 5^-1 (= ~904 cents), and another
with the pair 3^2 (= 9:8 = ~204 cents) and 3^-6 * 5^-1 (= ~202 cents).
There are several pairs of pitches separated by a
syntonic comma
(= ~21.5 cents), and in every case the two notes have different
symbols representing them.
Shown left to right are:
the tetrachord name and
extent, then the note name; then, a plot of the note's
pitch-height,
and the note's cents-value,
and 2,3,5-monzo,
all relative to the 1/1 mese,
which is at the vertical center.
Below are three views of a lattice in 2-3-5-space of
the entire modal-system gamut shown in Boethius's diagrams.
Here, the x,y,z axes represent respectively the generators
3/2, 5/4, and 2/1.
1) utilized a system of pitches related as 5-limit ratios, or
at least tuned closely enough to them to imply them,
2) recognized the "enharmonic equivalence" (in the modern sense)
of pitches separated by a skhisma,
3) recognized a distinction between pitches separated by a
syntonic comma.
If I'm correct that ancient Greek musicians *in practice* (i.e.,
in their actual musical notation) recognized the skhisma, then
it's no surprise at all that later Arab music-theorists picked
it up, as they did so many other ancient Greek concepts.
Here, the skhisma has been designated as a unison-vector – thus, the notes interpreted by Monzo can ignore skhisma differences, and can be viewed as a 19-tone chain-of-5ths from 3^-8 … 3^10, i.e., if A is the reference, the chain extends from Db to Fx.
Bower, Calvin M. (ed., trans.). 1989.
Boethius, Anicius Manlius Severinus. c. 505.
Hucbald of St. Amand. c. 880.
Warren Babb (trans.). 1978.
To:
Sent: Monday, December 03, 2001 4:04 PM
Subject: Re: [tuning] : The C-Fb-G major triad: Pythag-Just tuning.2
> To:
> Sent: Monday, December 03, 2001 2:49 PM
> Subject: [tuning] Re: Re : The C-Fb-G major triad: Pythag-Just tuning.2
>
>
> Pythagorean tuning is clearly based on a chain of fifths. The Arabic
> theorists simply lengthened this chain, perhaps to justify scales
> already in use that didn't fit the Greek mold. There is
>> circumstantial evidence that they stumbled upon the schisma (much as
> the West did later, around 1420), since they used it to construct,
> essentially, 5-limit just scales.
>>
>> ... [the synemmenon tetrachord] begins with its own trite
>> a semitone away from mese, then, after a tone, has a paranete
>> peculiar to itself, then, after another tone, has the nete synemmene,
>> which is in all respects of the same tension and sound
>> as paranete diezeugmenon.
>>
>> ... the paranete synemmenon
is the same in sound as trite diezeugmenon.
mese A n^0 1:1
> -9:8
lichanos meson G 3^-2 16:9
> -10:9
parhypate meson F 5^-1 8:5
>> -16:15
hypate meson E 3^1 3:2
My pitch-height and
monzo
analysis of one mode of the entire
Perfect Immutable System,
in the diatonic genus,
is given in the graph below.

Note the synemmenon
tetrachord's
"paranete
peculiar to itself" (294 cents,
compared to ~316 cents for the trite
diezeugmenon),
as described by Nicomachus.
Below is a
lattice of the system in
2,3,5-prime-space.
Each monzo in the graph above
determines the location of the
pitch's cube in the lattice;
the cubes are labeled with cents-values.
The x,y,z axes represent respectively the prime-factors 2, 3, and 5.

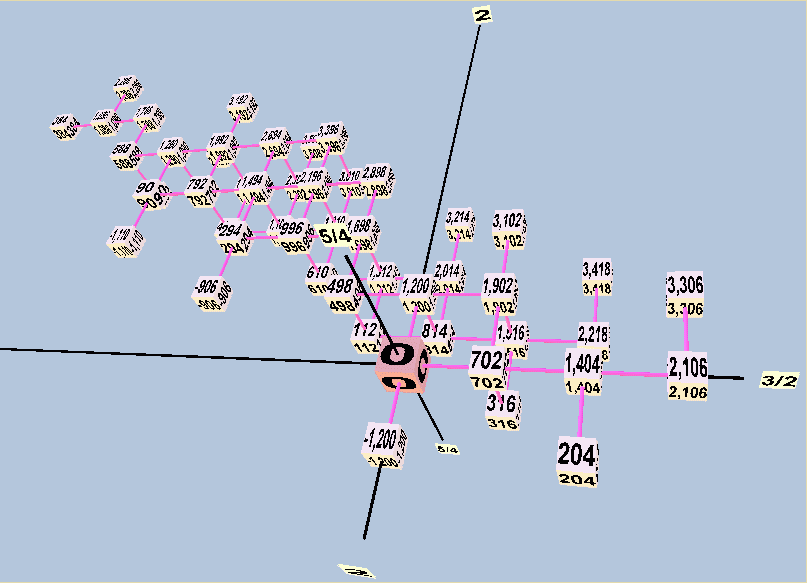
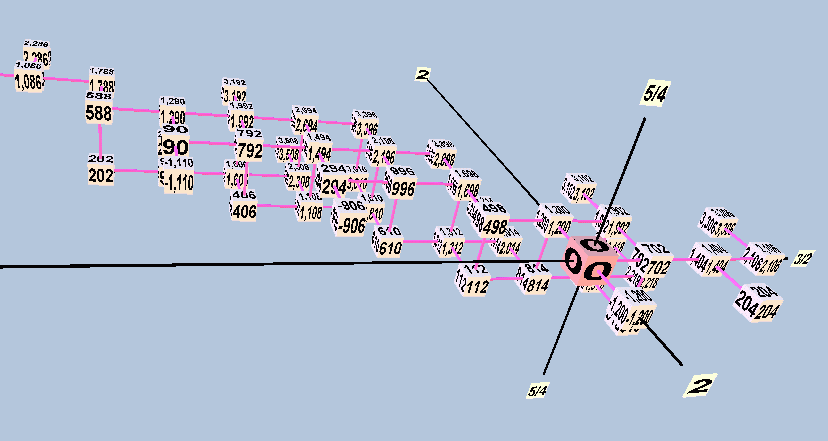
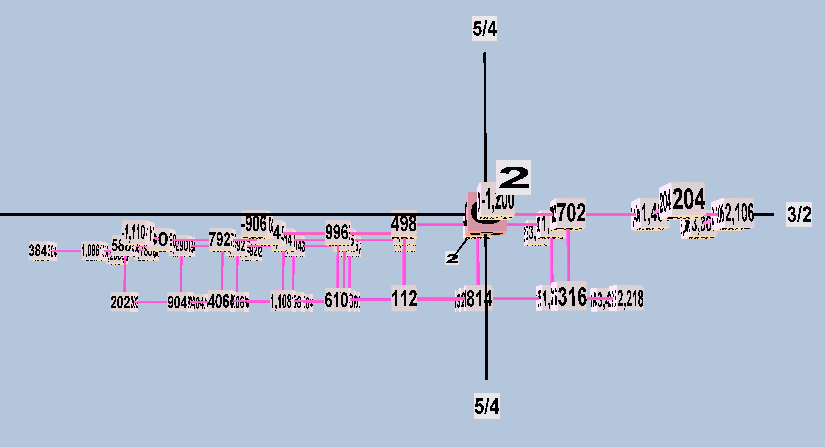
Taken together, and assuming that the tuning of Didymus
is correct, I believe the evidence of the Greek-letter notation
indicates that musicians of the late classical and early post-classical
period (c. 100 BC - 500 AD):
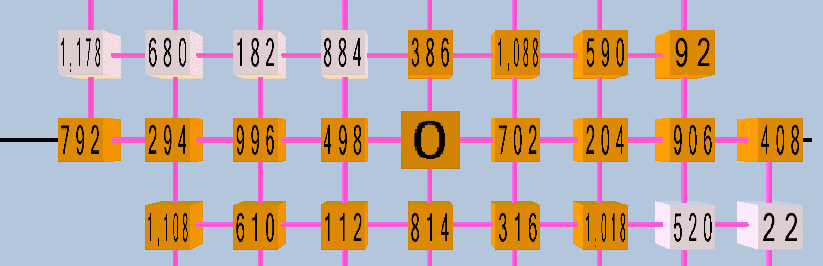
REFERENCES
Barker, Andrew (ed.). 1989.
Greek Musical Writings.
Vol. 2: Harmonic and Acoustic Theory.
Cambridge Readings in the Literature of Music,
Cambridge Univ. Press, Cambridge.
Boethius: "Fundamentals of Music".
Music Theory Translation Series, ed. Claude Palisca.
Yale University press, new Haven & London.
ISBN: 0-300-03943-3
L.o.C.#: MT5.5.B613
in Friedlein, Godofredus (ed.). 1867.
Boethii De institutione musica libri quinque.
B. G. Teubner, Leipzig.
http://www.music.indiana.edu/tml/6th-8th/BOEMUS4_TEXT.html
De harmonica institutione.
E. de Coussemaker (ed.), Durand, Paris, 1866-1876.
http://www.music.indiana.edu/tml/9th-11th/HUCHAR_TEXT.html
Hucbald, Guido, and John on music : three medieval treatises.
Edited, with introductions, by Claude V. Palisca;
index of chants by Alejandro Enrique Planchart.
New Haven : Yale University Press.
(Music Theory Translation Series, 3)
ISBN: 0300020406
L.o.C.#: ML170 .H82
Updated:
2004.07.15 -- page created from older documents
2004.09.03 -- expanded, with diagrams added
2005.06.19 -- added 19-tone chain-of-5ths interpretation
2005.11.22 -- added three views of 2-3-5-space lattice of complete modal gamut
feedback
-- page created from older documents
2004.09.03 -- expanded, with diagrams added
2005.06.19 -- added 19-tone chain-of-5ths interpretation
2005.11.22 -- added three views of 2-3-5-space lattice of complete modal gamut