La mejor manera que he descubierto para agarrar tanta información armónica como posible en una apenas-entonación el sistema que templa musical es el uso de los diagramas del cedazo que retratan echadas como puntas en el espacio multidimensional conectado por vectores.
En un sistema que templa de la apenas-entonación, cada nota es representada por una relación de transformación que describa el lazo de esa nota a otra nota, generalmente una que se utilice como referencia para el sistema entero. Este tono de la referencia tiene la relación de transformación 1/1, también descrita como 1:1 o 1 a 1.
Cualquier número poder ser descomponer en factores en serie primero número, cada que ser uno base que tener uno exponente que ser cualquier positivo o negativo, representing número > 1 o <1, respectively, unless the exponent=0, which represents 1, the identity in multiplication.
potencia 2 ser todo armónicamente equivalente este identidad 1, así, potencia 2 representar "octava", y así tener ninguno pronunciado efecto en armonía, y poder ser eliminar, a menos que " octava " registro ser específico bajo consideración. Por lo tanto los diagramas comienzan normalmente con la primero-base 3.
Mi cedazo diagrama tratar cada primero base como
uno único dimensión en espacio, con todo exponente irradiar hacia
fuera central 1/1, que ser equivalente todo número 0th potencia, o n0.
Considerado en espacio de 2 dimensiones, los vectores que
conectan cada recorrido del exponente adentro en una dirección única
para cada uno prima. Esta dirección es determinada por el ángulo
que representa
el valor de los centavos (dentro de
la " octava ") de eso prima a la 1ra potencia, empezando con las 6 de
la posición. Así, 31, que es la relación de
transformación 3/2 y es 702 centavos, tiene un vector el irradiar
hacia fuera a partir de la 1/1 en muy cerca de la posición de las 1.
51, que es la relación de transformación 5/4 y
es 386 centavos, tiene un vector el irradiar hacia fuera apenas menos
de a las 10 de la posición, etcétera. Los exponentes negativos
irradian simplemente hacia fuera de la dirección opuesta.
Los vectores también varían en longitud y espesor según
las primero-bases que están conectando, con 3 el más corto y lo más
densamente posible.
Interestingly, aunque el espacio de 2 dimensiones era el
entorno en el cual estas medidas fueron hechas, aparecen ellas ojo
formar 3 o aún más - las estructuras dimensionales, asemejándose
algo a cristales.
Harry Partch inventó una estructura que él llamó el "diamante de la tonalidad". Este
mostrar todo armónico lazo relación de transformación con número
bajo uno cierto "impar límite " (excepto " octava
doubling ", o multiplicación por 2, que él used guardar cada
relación de transformación dentro mismo " octava ", como en más
generalmente fuente escalar).
Estos " diamantes ", que consiguen más grandes y llevan a
cabo simplemente exponencial más relaciones de transformación con
cada nuevo otro impar-límite en la versión de Partch, toma en un
aspecto totalmente diverso cuando está ilustrado usando mis cedazos.
El proceso abroga ciertamente a mis sensibilidades artísticas.
Ilustro aquí el 5-Limit, el 7-Limit, el 9-Limit, el
11-Limit, y el 13-Limit " diamantes de la tonalidad " según lo
representado por mis diagramas del cedazo. La simetría que Partch
conocido en sus escalas y diamantes de la tonalidad es fácilmente
evidente aquí, aunque los diamantes de la tonalidad en esta
representación no son perfectamente
simétricos, al
igual que algunos otros sistemas yo han ideado.
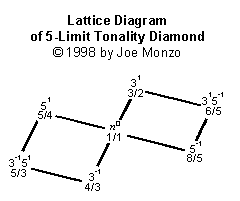
Partch llamar éste incipiente tonalidad diamante, porque uno tríada con proporción 4:5:6 dar máximo consonance para uno acorde con tres distinto identidad, así éste ser simple sistema que poder ser construir que dar cualquier verdadero sensación tonalidad.
La tríada " principal " en mi cedazo parece esto (con los odentities dados):
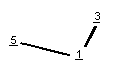
y la tríada " de menor importancia " parece esto (con udentities):
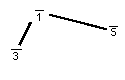
Observe que el cedazo 5-Limit o el diamante contiene 3 por cada uno del " comandante " y de tríadas " de menor importancia ". Cada n- El sistema del límite contiene siempre (n+1) acordes del consonance máximo, cada uno con (las identidadesde n +1)/2, divididas uniformemente en (n+1)/2 cada uno del " comandante " y del " menor de edad ".
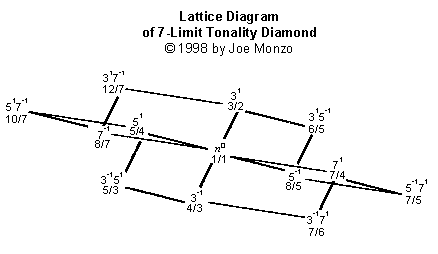

Observe que el cedazo 9-Limit no tiene una nueva dimensión
-- agrega simplemente una capa, en cualquier final de las potencias de
3, sobre el cedazo 7-Limit. Éste ser porque 9 ser no
uno primero número, pero algo uno compuesto, es
decir, uno número componer otro preparar, en este caso
3 x 3, o 32.
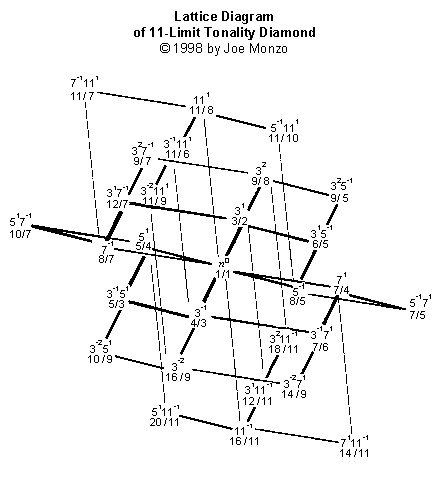
Aquí está una versión del cedazo 11-Limit en color
completo:
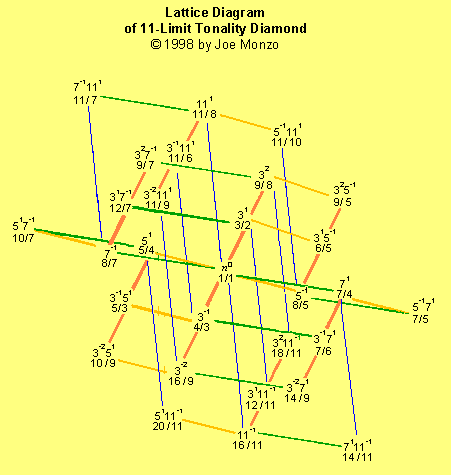
(éste puede parecer mejor en su sistema,
pero lleva un rato la transferencia directa.)
Está después una versión sombreada del cedazo 11-Limit de
que tengo gusto sobretodo:
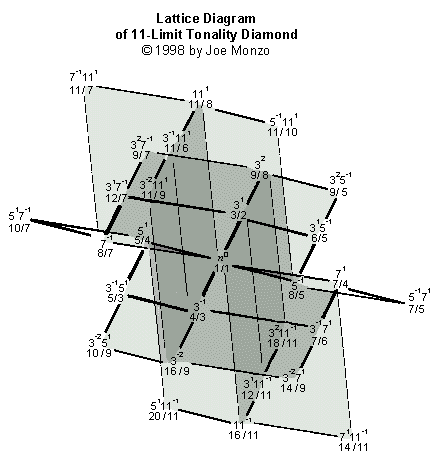
Y el más complicado de esto fije, el cedazo 13-Limit:
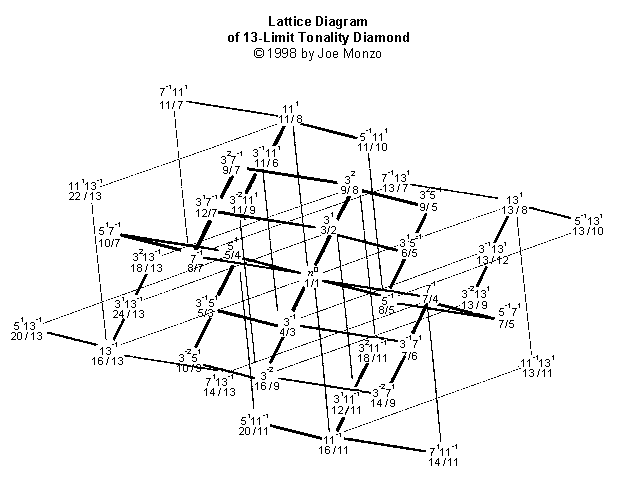
Los cedazos forman intrincado cristal-como las estructuras que muestran una abundancia de la información armónica de un vistazo. Si ser ver en orden enumerar arriba, él poder ser ver que cada uno pequeño uno ser contener dentro grande uno.
