Joe Monzo's
Harmonic Lattice Diagrams
MouseOver applet by
Ming Sun Ho
MING'S APPLET APPEARS HERE, AT THE BOTTOM OF THIS PAGE
Ming's applet portrays visually the finity displayed by Partch's theory of odd-limit Tonality Diamonds, characterized as a 'breakthrough' in JI theory by Brian McLaren.
McLaren wrote:
Thinking of just intonation in terms of subdividing a string produces problems for the JI music theory. One of the most basic dilemmas is that (prior to Partch) no theorist could justify using a particular just intonation. Many just intonation theorists offered many different systems, but each one was arbitrary. No just tuning system was both musically sufficient and theoretically necessary.
This arises from the nature of string subdivisions. Once one begins to section off a string, there is no necessary stopping point; one can continue to infinity. Moreover, once one fixes some member of the harmonic series as the highest prime used in a just ratio, one immediately faces the question: Why? If three divisions of the tetrachord are good, why not 4? Why not 5? Why not 93? If 7 is a good JI limit, why isn't 11 better? If 13 is better still, why not 17? And so on, up to infinity. [emphasis Monzo's]
This led to endless debate between just intonation theorists. Which scale was best? Which limit was most musical? The acrimony and arguments tended to drown out the music, leaving the impression that just intonation theory prior to Partch was a "Serbonian bog into which whole armies of musical-minded mathematicians and mathematically-minded musicians have disappeared without a trace." [James Clerk Maxwell, Rede Lecture, 1867]
This traditional Greek approach to just intonation dominated microtonal JI theory from the time of Ptolemy in 100 A.D. It ruled europe through Boethius circa 600 A.D. up to the time of Prosdocimus to Vicentino and Mersenne, onward to Helmholtz, Ellis and Bosanquet in the 1800s...and the obsession with Greek theories of just intonation remained very much alive and well when Harry Partch wrote his breakthrough Exposition of Monophony in 1927-1933.
Partch's "Exposition" represents a breakthrough because, for the first time, Partch reached beyond the Greek method of just intonation scale construction by string subdivision.
Instead, Partch introduced a more sophisticated way of constructing just scales. He set out the first N members of the harmonic series and multiplied them by the first N members of the subharmonic series, generating a set of (N2 - N) - 1 pitches.
(If N = 6, N2 - N - 1 = 29). Partch called this a "tonality diamond" (because he turned the square on its side to form a diamond).In one leap, Partch introduced an entirely new functional method of generating just intonation scales. Subsequent theorists were no longer limited to conceiving of just scales as string subdivision.; Instead, they could now view just intonation scales as cyclic groups generated by mathematical functions operating on sets of integers. (In the case of Partch's tonality diamond, the functions concerned are y = x and y = 1/x functions and the set is a sub-group of positive odd integers).
By introducing the concept of the tonality diamond, Partch immediately gave just intonation composers a rationale for their scales: Partch's diamond pitches are necessarily limited to a specific group of (N2 - N) - 1 pitches, where N is the number of integers in the generating set. For the first time, just intonation composers knew where to stop. For the first time, they had a theoretically necessary and musically coherent set of scale pitches which did not arise ex nihilio, from the theorist's whim.
Most subsequent just intonation theory flows from Partch's crucial insight. His breakthrough: the realization that just scales construction could be reformulated as mathematical functions operating on subsets of the integers. Since 1933, it has become commonplace for just intonation music theorists to speak of "generating sets" and operations performed on them.
[for example, see CPS]
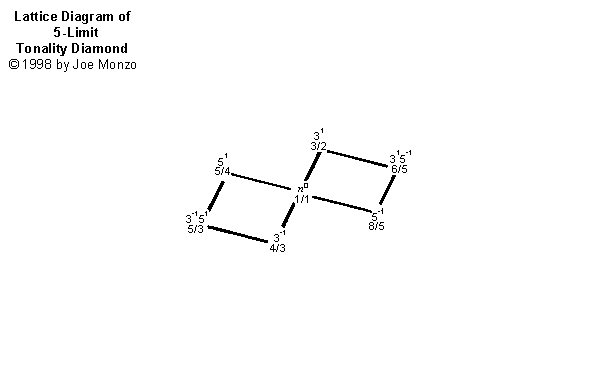
Ming wrote the rollover script so that it starts with my lattice representation of the 5-Limit Tonality Diamond.
Each subsequent higher-odd-limit lattice is centered on the same 5-Limit Diamond, and if you hold the cursor over the links that specify the different limits, you can see the addition of ratios to the system visually.
You can see how the complexity and the finity of the system as a whole increases as the odd-limit is increased.
So I like it because of my interest in finity.
McLaren emphasizes this as one of the most important aspects (perhaps the most important?) of Partch's theoretical work.
And it also models the changing complexity of the various limits.
MING'S APPLET APPEARS HERE, AT THE BOTTOM OF THIS PAGE
MouseOver these links to reveal
5
7
9
11
13
limit.

I welcome feedback about this webpage.
|