In this webpage, I present several different lattice diagrams which plot various fraction-of-a-comma meantone-like systems on a JI lattice with prime-factor axes of 3 and 5.

The meantone chain forms its own linear axis on the lattice, and makes it easy to visualize which JI ratios are acoustically the most closely implied by the meantone pitches. The meantone pitch-classes are called by their generator number. These lattices are "8ve"-invariant, that is, prime-factor 2 is ignored.

CAVEAT: Compositional practice may insist that a meantone pitch implies a different JI ratio than the one which is acoustically the closest.

These lattices are given with the reference pitch of C = n⁰.

In every case, the list of implied JI ratios includes both of the two nearest, except for instances where the meantone tuning gives one exact ratio (as, for example, the +3, +6, +9 generators A, F#, D# of 1/3-comma; the +7 generator C# of 2/7-comma; the +4, +8, +12 generators E, G#, B# of 1/4-comma; the +5, +10 generators B, A# of 1/5-comma; etc.).

The lattice diagrams, however, only give two ratios in cases where the meantone is exactly at the midpoint between them (as with the +2 generator "D" in 1/4-comma meantone, and with the +3 generator "A" in 1/6-comma meantone); otherwise only the nearest JI implied ratio is given.

The meantone chains could be extended beyond my diagrams; I chose a 27-note chain of +/- 13 generators (Gbb to Fx) as an arbitrary limit in every example.

1/3-comma

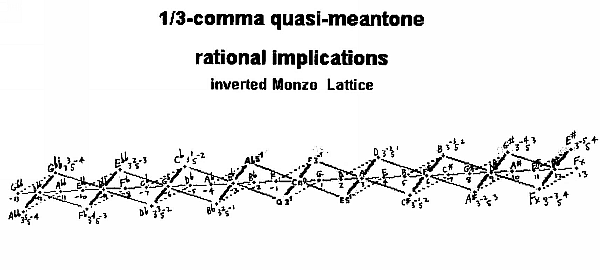
In the 1/3-comma quasi-meantone, the generator is 1/3-comma narrower than 3:2. Thus, the +1 generator is 1/3-comma flatter than G 3:2 (= 3¹) and 2/3-comma sharper than G 40:27 (= 3^-35¹).

The next note in the chain (the +2 generator) is 2/3-comma flatter than D 9:8 (= 3²). Since 2/3-comma is more than 1/2-comma, it is evident that the +2 generator will be closer to the note a comma flatter than 9:8 (= 10:9 ratio = 3^-25¹), namely, 1/3-comma sharper than D 10:9.

The +3 generator is exactly the JI ratio A 5:3 (= 3^-15¹).



2/7-comma

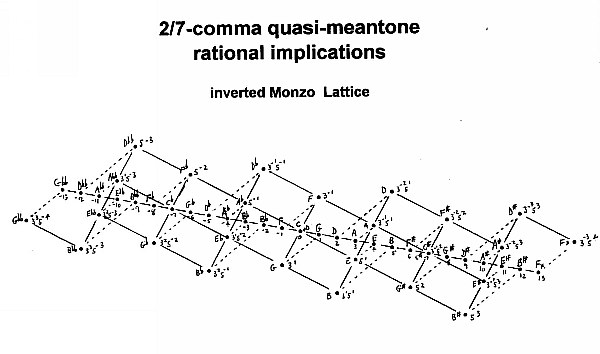
In the 2/7-comma quasi-meantone, the generator is 2/7-comma narrower than 3:2. Thus, the +1 generator is 2/7-comma flatter than G 3:2 (= 3¹) and 5/7-comma sharper than G 40:27 (= 3^-35¹).

The next note in the chain (the +2 generator) is 4/7-comma flatter than 9:8 (= 3²). Since 4/7-comma is more than 1/2-comma, it is evident that the +2 generator will be closer to the note a comma flatter than 9:8 (= 10:9 ratio = (= 3^-25¹), namely, 3/7-comma sharper.

The +3 generator is 6/7-comma flatter than A 27:16 (= 3³) and only 1/7-comma sharper than A 5:3 (= 3^-15¹).

The +4 generator is 1/7-comma flatter than E 5:4 (= 5¹)and 6/7-comma sharper than E 100:81 (= 3^-45²).

The +5 generator is 3/7-comma flatter than B 15:8 (= 3¹5¹) and 4/7-comma sharper than B 50:27 (= 3^-35²).

The +6 generator is 5/7-comma flatter than F# 45:32 (= 3²5¹) and 2/7-comma sharper than F# 25:18 (= 3^-25²).

The +7 generator is exactly the JI ratio C# 25:24 (= 3^-15²).



1/4-comma

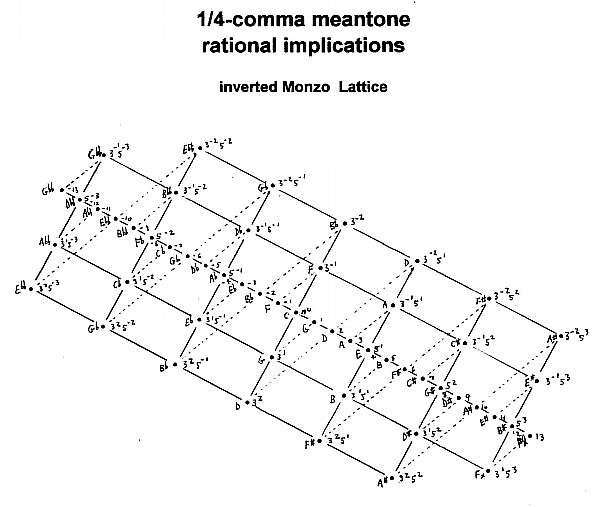
In the 1/4-comma meantone, the generator is 1/4-comma narrower than 3:2. Thus, the +1 generator is 1/4-comma flatter than G 3:2 (= 3¹) and 3/4-comma sharper than G 40:27 (= 3^-35¹).

The next note in the chain (the +2 generator) is 1/2-comma flatter than D 9:8 (= 3²) and 1/2-comma sharper than D 10:9 (= 3^-25¹). Thus, this is exactly the "mean tone" between the two JI "whole-tones".

The +3 generator is 3/4-comma flatter than A 27:16 (= 3³) and 1/4-comma sharper than A 5:3 (= 3^-15¹) .

The +4 generator is exactly the JI ratio E 5:4 (= 5¹).



1/5-comma

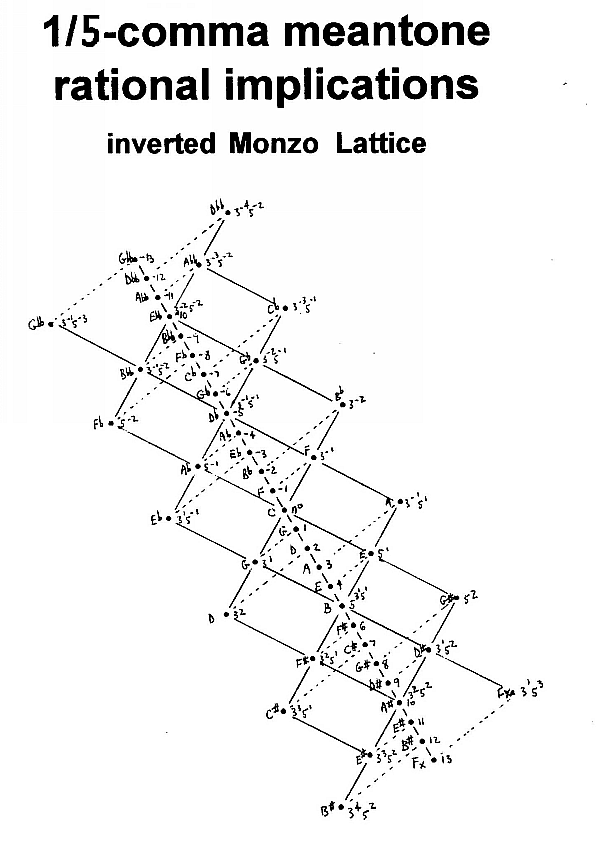
In the 1/5-comma quasi-meantone, the generator is 1/5-comma narrower than 3:2. Thus, the +1 generator is 1/5-comma flatter than G 3:2 (= 3¹) and 4/5-comma sharper than G 40:27 (= 3^-35¹).

The next note in the chain (the +2 generator) is 2/5-comma flatter than 9:8 (= 3²). and 3/5-comma sharper than 10:9 (= 3^-25¹).

The +3 generator is 3/5-comma flatter than A 27:16 (= 3³) and 2/5-comma sharper than A 5:3 (= 3^-15¹) .

The +4 generator is 4/5-comma flatter than E 81:64 (= 3⁴)and 1/5-comma sharper than E 5:4 (= 5¹).

The +5 generator is exactly the JI ratio B 15:8 (= 3¹5¹).



1/6-comma

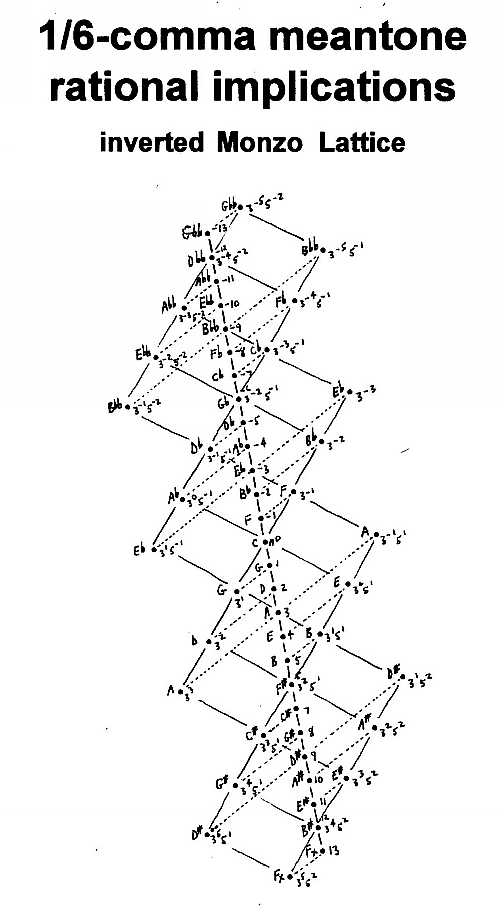
In the 1/6-comma quasi-meantone, the generator is 1/6-comma narrower than 3:2. Thus, the +1 generator is 1/6-comma flatter than G 3:2 (= 3¹) and 5/6-comma sharper than G 40:27 (= 3^-35¹).

The next note in the chain (the +2 generator) is 1/3-comma flatter than 9:8 (= 3²) and 2/3-comma sharper than 10:9 (= 3^-25¹).

The +3 generator is 1/2-comma flatter than A 27:16 (= 3³) and 1/2-comma sharper than A 5:3 (= 3^-15¹). Thus, it is precisely the mean "6th" between the two JI ratios.

The +4 generator is 2/3-comma flatter than E 81:64 (= 3⁴)and 1/3-comma sharper than E 5:4 (= 5¹).

The +5 generator is 5/6-comma flatter than B 243:128 (= 3⁵)and 1/6-comma sharper than B 15:8 (= 3¹5¹).

The +6 generator is exactly the JI ratio F# 45:32 (= 3²5¹).



And here is a more accurate lattice of the above, showing a closed 55-tone 1/6-comma meantone chain and its implied pitches, all enclosed within a complete periodicity-block defined by the two unison-vectors 81:80 = [-4 4 -1] (the syntonic comma, the shorter boundary extending from south-west to north-east on this diagram) and [-51 19 9] (the long nearly vertical boundary), portrayed here as the white area.

For the bounding corners of the periodicity-block, I arbitrarily chose the lattice coordinates [-7.5 -5] for the north-west corner, [-11.5 -4] for north-east, [11.5 4] for south-west, and [7.5 5] for south-east. This produces a 55-tone system centered on n⁰.

The grey area represents the part of the JI lattice outside the defined periodicity-block (and thus, with each of those pitch-classes in its own periodicity-block), and the lattice should be imagined as extending infinitely in all four directions. The other periodicity-blocks, all identical to this one, can be tiled against it to cover the entire space.



1/11-comma

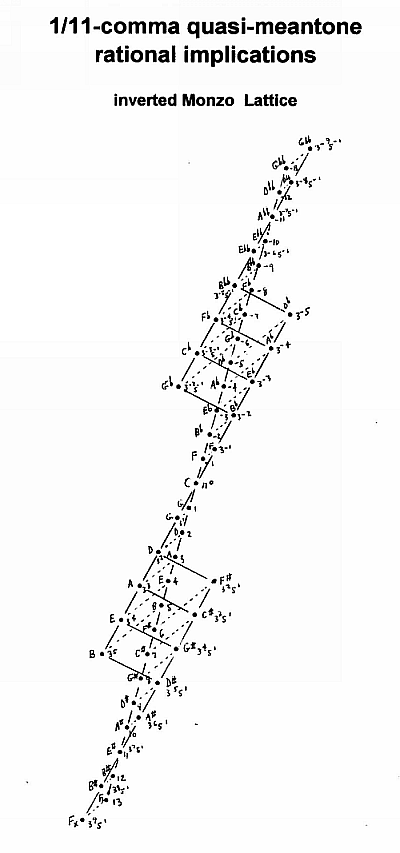
In the 1/11-comma quasi-meantone, which is audibly indistinguishable from the usual 12-EDO tuning, the generator is 1/11-comma narrower than 3:2. Thus, the +1 generator is 1/11-comma flatter than G 3:2 (= 3¹) and 10/11-comma sharper than G 40:27 (= 3^-35¹).

The +2 generator is 2/11-comma flatter than 9:8 (= 3²) and 9/11-comma sharper than 10:9 (= 3^-25¹).

The +3 generator is 3/11-comma flatter than A 27:16 (= 3³) and only 8/11-comma sharper than A 5:3 (= 3^-15¹).

The +4 generator is 4/11-comma flatter than E 81:64 (= 3⁴)and 7/11-comma sharper than E 5:4 (= 5¹).

The +5 generator is 5/11-comma flatter than B 243:128 (= 3⁵) and 6/11-comma sharper than B 15:8 (= 3¹5¹).

The +6 generator is 6/11-comma flatter than F# 729:512 (= 3⁶) and 5/11-comma sharper than F# 45:32 (= 3²5¹).

The +7 generator is 7/11-comma flatter than C# 2187:2048 (= 3⁷) and 4/11-comma sharper than C# 135:128 (= 3³5¹).

The +8 generator is 8/11-comma flatter than G# 6561:4096 (= 3⁸) and 3/11-comma sharper than G# 405:256 (= 3⁴5¹).

The +9 generator is 9/11-comma flatter than D# 19683:16384 (= 3⁹) and 2/11-comma sharper than D# 1215:1024 (= 3⁵5¹).

The +10 generator is 10/11-comma flatter than A# 59049:32768 (= 3¹⁰) and 1/11-comma sharper than A# 3645:2048 (= 3⁶5¹).

The +11 generator is exactly the JI ratio E# 10935:8192 (= 3⁷5¹).

Note that because the JI lattice implied by 1/11-comma meantone includes the skhisma, the chain effectively closes at 12 tones; a typical version could be -3 Eb to +8 G#.



See also: Ellis's Duodene and a "best-fit" meantone.

updated:

2000.12.09