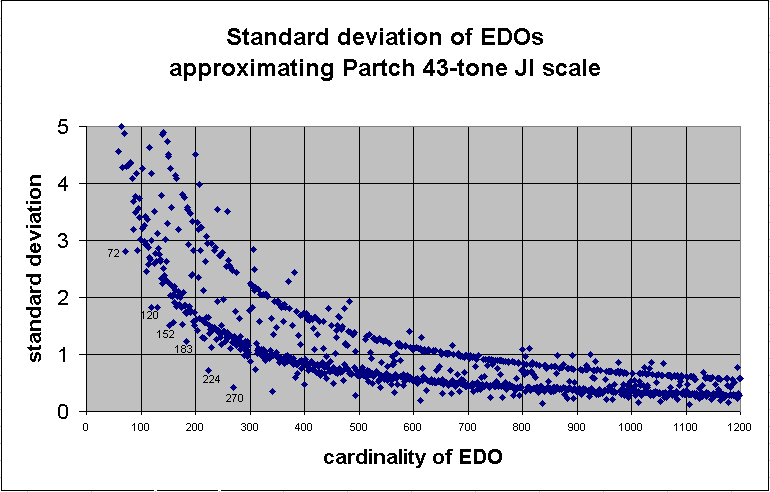
American composer Harry Partch (1901-1974) based all of his mature musical compositions on a musical scale tuned in just intonation and based on the 11-limit tonality diamond, played on instruments he designed and built himself to be played in that tuning. The number of notes varied for a time from about 29 to 55, until he finally settled on a scale of 43 tones to the octave (his identity interval, which Partch always referred to by its frequency ratio 2/1).
Partch's tuning is often called "extended just intonation", because traditional just intonation used ratios with only the prime-factors 2, 3, and 5, whereas Partch added 7 and 11 to these.
Below is a tabulation of the scale, with the 2,3,5,7,11-monzo, ratio, and approximate cents value, for each pitch. Next to the table is a graph showing the pitch-height of the ratios.
2,3,5,7,11-monzo ratio ~cents [ 1 0, 0 0 0 > 2 / 1 1200.0 [ 5 -4, 1 0 0 > 160 / 81 1178.49371 [ 6 -1, 0 0 -1 > 64 / 33 1146.727057 [ 3 -1, 1 -1 0 > 40 / 21 1115.532807 [-3 1, 1 0 0 > 15 / 8 1088.268715 [-1 -1, 0 0 1 > 11 / 6 1049.362941 [ 2 0, 1 0 -1 > 20 / 11 1034.995772 [ 0 2, -1 0 0 > 9 / 5 1017.596288 [ 4 -2, 0 0 0 > 16 / 9 996.0899983 [-2 0, 0 1 0 > 7 / 4 968.8259065 [ 2 1, 0 -1 0 > 12 / 7 933.1290944 [-4 3, 0 0 0 > 27 / 16 905.8650026 [ 0 -1, 1 0 0 > 5 / 3 884.358713 [ 1 2, 0 0 -1 > 18 / 11 852.5920594 [ 3 0, -1 0 0 > 8 / 5 813.6862861 [ 0 0, 0 -1 1 > 11 / 7 782.4920359 [ 1 -2, 0 1 0 > 14 / 9 764.9159047 [ 5 -1, 0 -1 0 > 32 / 21 729.2190927 [-1 1, 0 0 0 > 3 / 2 701.9550009 [ 3 -3, 1 0 0 > 40 / 27 680.4487113 [ 4 0, 0 0 -1 > 16 / 11 648.6820576 [ 1 0, 1 -1 0 > 10 / 7 617.4878074 [ 0 0, -1 1 0 > 7 / 5 582.5121926 [-3 0, 0 0 1 > 11 / 8 551.3179424 [-2 3, -1 0 0 > 27 / 20 519.5512887 [ 2 -1, 0 0 0 > 4 / 3 498.0449991 [-4 1, 0 1 0 > 21 / 16 470.7809073 [ 0 2, 0 -1 0 > 9 / 7 435.0840953 [ 1 0, 0 1 -1 > 14 / 11 417.5079641 [-2 0, 1 0 0 > 5 / 4 386.3137139 [ 0 -2, 0 0 1 > 11 / 9 347.4079406 [ 1 1, -1 0 0 > 6 / 5 315.641287 [ 5 -3, 0 0 0 > 32 / 27 294.1349974 [-1 -1, 0 1 0 > 7 / 6 266.8709056 [ 3 0, 0 -1 0 > 8 / 7 231.1740935 [-3 2, 0 0 0 > 9 / 8 203.9100017 [ 1 -2, 1 0 0 > 10 / 9 182.4037121 [-1 0, -1 0 1 > 11 / 10 165.0042285 [ 2 1, 0 0 -1 > 12 / 11 150.6370585 [ 4 -1, -1 0 0 > 16 / 15 111.7312853 [-2 1, -1 1 0 > 21 / 20 84.46719347 [-5 1, 0 0 1 > 33 / 32 53.27294323 [-4 4, -1 0 0 > 81 / 80 21.5062896 [ 0 0, 0 0 0 > 1 / 1 0.0 |

|
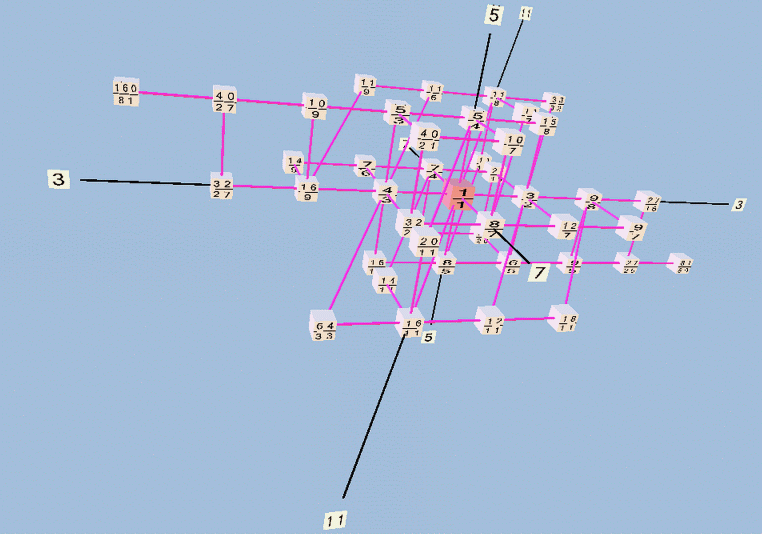
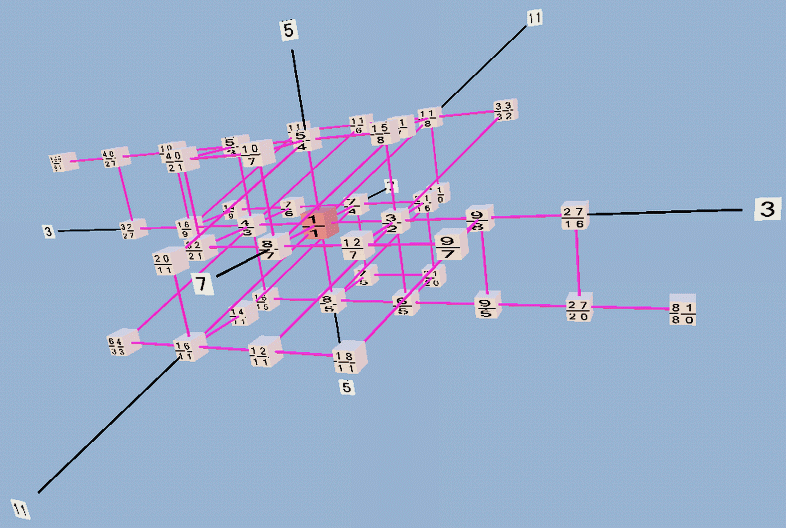
Below are two views of a Tonescape lattice diagram of Partch's 43-tone just intonation scale; it is a 3-dimensional projection of a 4-dimensional lattice, with axes representing prime-factors 3, 5, 7, 11.
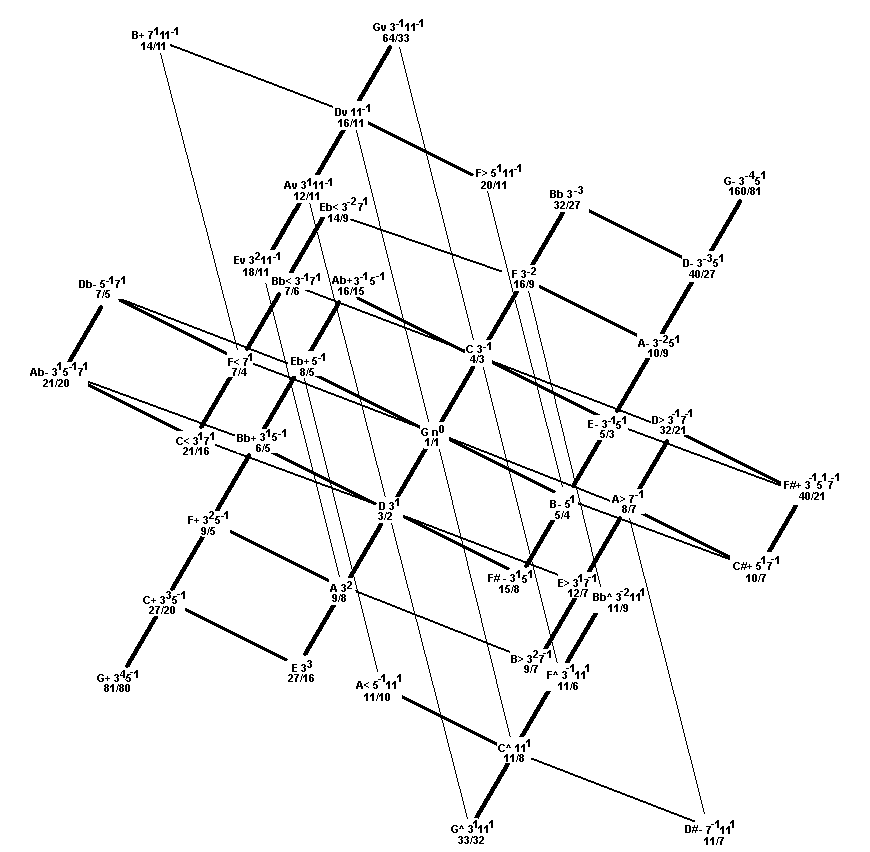
Below is an inverted Monzo lattice of Harry Partch's 43-tone JI scale. Pitches are notated in three formats:
- the 72edo version of HEWM (the letters and accidental symbols);
- the [3 5 7 11] prime-factor vector (the prime factors and their exponents); and
- the ratio (written as a fraction),
which is what Partch himself used.
First, the plain lattice:
Next, a shaded version which portrays more readily
the 4-dimensionality of the lattice by coloring
the planes of the lattice -- each of which
incorporates two of the four
prime-factors
3, 5, 7, and 11 --
as tho they were panes of transparent tinted glass: