In GREEN, Monzo's English version of Prof. Bailhache's French translation of Euler's Latin (contributed specifically for this translation).
In MAGENTA (at the end), the translator's notes, and observations from others.
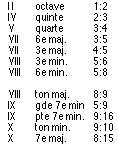
By the middle of the 1700s, at the time when the music known as classical acquires its letters of nobility with Bach (1685-1750), Handel (1685-1759), Rameau (1683-1764), Haydn (1732-1809), Mozart (1756-1791), etc., two particularly famous mathematicians, Euler and d'Alembert, produce theories of music. This fact is obviously not the result of a "historical chance". It represents on the contrary the prolongation of one tradition.1 By the end of the previous century, several scientists had already become intrigued and put their attention on the same subject: Descartes (Compendium musicae), Galileo (end of the 1st day of Discorsi), Mersenne (the enormous work of the Universal Harmony), Leibniz "as an amateur".2 But in the 1700s, it is the music itself which changes, the traditional harmony dethroning the medieval counterpoint definitively. Thus this change had to be explained, to make the theory of it, and the task could inspire, rightly, any scientist set on music.
Euler (1707-1783) is 24 years old when he writes, in 1731, his
Tentamen novae theoriae musicae ex certissimis harmoniae
principiis dilucide expositae (A attempt at a new
theory of music, exposed in all clearness according to
the most well-founded principles of harmony).
It is a work of 263
pages, written in Latin, which will be published only in 1739. It was
translated into French one century later with the edition of Brussels
of works of the mathematician. I will presently say some words on the
quality of this translation.
In 1739 Euler is already known as a mathematician and is in
St Petersburg, where he will soon occupy the Chair of mathematics.
He is extremely interested by all that touches on music.
He published in Basle, in 1727, a "thesis on sound" where he
compares the sounds produced by the vibrating cords with those
generated by the wind instruments. And about 1726 already, Euler had
projected the plan of a considerable work on music. Apart from
the fact that the sounds were to be noted there by sequence numbers in
the scale, the object of study remained close to musical realities.
The last section, for example, was to analyze the various kinds of
pieces of music (saraband, courrant, etc). But the departure of the
mathematician for St Petersburg (1727) and his other work prevented
him from proceeding in this initial way. It is finally a much
more mature work which was born in 1739.3
Euler remained all the rest of his life interested by
the questions of music. He brought precise details to his new theory
with some articles4
showing, as we will see, that he could take
account of criticisms which one had addressed to his conceptions.5
Plus, I even believe and I will try to show it that he gave up one of
the fundamental assumptions of his theory, without acknowledging it
expressly. Passing on the first chapter (on sound and hearing), I
come immediately to the bases of Euler's musical theory
(he talks in the second chapter "de suavitate et principiis harmoniae").
How to explain that certain sounds appear pleasant and others
not? It seems paradoxical to find a rule, since everyone does not
like the same things, or the taste of the same person can evolve.
Can one lock up an art, like music, in laws? Euler answers that,
as for all the fine arts, it is necessary to trust the opinion of
enlightened people,
therefore in music those whose ear was exerted and who will be
able to see the right laws which dictates nature:
"Sed Musicum similem se genere oportet Architecto, qui plurimorum
perversa de aedificiis iudicia non curans secundum certas et in
natura ipsa fundatas leges aedes exstruit; quae etiamsi harum rerum
ignaris non placeant, tamen, dum intelligentibus probentur, contentus
est." [OO, 3a, I, 224]
["We will answer that the musician must
act like the architect who, worrying little about the bad judgements
which the ignorant multitudes pass on the buildings , builds according
to unquestionable laws based on nature, and is satisfied with
the approval of the people who are enightened in this matter."
This preliminary remark being made, Euler affirms that any
pleasure comes from the perception of the perfection,
any normally-constituted person seeking this:
"Certum est enim perceptionem perfectionis voluptatem
parere hocque omnium spirituum esse proprium, ut perfectionibus
detegendis et intuendis delectentur, ea vero omnia, in quibus vel
perfectionem deficere vel imperfectionem adesse intelligunt,
aversentur." [OO, 3a, I, 225]
["It is certain that any perception of perfection
gives birth to pleasure and that it is a property common
to every spirit, as much to delight itself with the discovery
and contemplation of a perfect object, as to avoid what misses
perfection or exposes its imperfections."
- Bailhache/Monzo]
However, as the example of a clock shows us,
perfection is reduced to order.
"Contemplemur exempli causa horologium, cuius finis
est temporis partes et divisiones ostendere: id maxime nobis
placebit, si ex eius structura intelligimus omnes eius partes ita
esse confectas et inter se conjunctas, ut omnes ad tempus exacte
indicandum concurrant."
[Let us take for example a clock,
whose destination is to mark divisions of time;
we will like it with the highest degree, if the
examination of the structure makes us understand
that the various parts are laid out and combined
by it in such a way that all contribute to indicate
time with exactitude.
"Vicissim igitur etiam intelligitur, ubi sit ordo, ibi etiam esse
perfectionem et legem regulamve ordinis respondere scopo perfectionem
efficienti." [OO, 3a, I, 226]
[Reciprocally, one can say that
where there is order, there is perfection, and
that the rule or law of the order corresponds
to the goal which marks the perfection.
- Bailhache/Monzo]
This notion of order is the key to the theory.
However, it still remains to adapt it to the field of music.
The order of things can be perceived in two ways:
either one knows already the rules and one recognizes the presence
of it immediately; or the rules are unknown, and one must then
seek them, to reveal them (detego); music conforms
to this second process:
"Duobus autem modis ordinem percipere possumus;
altero, quo lex vel regula nobis iam est cognita, et ad eam rem
propositam examinamus; altero, quo legem ante nescimus atque ex ipsa
partium rei dispositione inquirimus, quaenam ea sit lex, quae istam
structuram produxerit. Exemplum horologii supra allatum ad modum
priorem pertinet; iam enim est cognitus scopus seu lex partium
dispositionis, quae est temporis indicatio; ideoque horologium
examinantes dispicere debemus, an structura talis sit, qualem scopus
requirit. Sed si numerorum seriem aliquam ut hanc 1, 2, 3, 5, 8, 13,
21 etc. ascipio nescius, quae eorum progressionis sit lex, tum
paullatim eos numeros inter se conferens deprehendo quemlibet esse
duorum antecedentium summam hancque esse legem
eorum ordinis affirmo."
["There are two ways in which we are able to perceive order;
the one, in which the law or rule is already known to us,
and to that matter being proposed, we simply examine;
the other, in which the law before we were ignorant and
out of the regular arrangement of parts we inquire,
so that that we may construct laws. The example of the clock given
above belongs to the first sort; one already knows the goal
or law of the regular arrangement of the parts, which is the indication of
a time value; thus on examining a clock we only need to discern,
whether its structure is such, as this goal demands.
But if the number series somehow were this 1, 2, 3, 5, 8, 13, 21 etc.
and we had to consider unaware, what is the law of their progression,
then gradually the comparison of those numbers among themselves
will allow anyone to discover that each is the sum of
the two previous and consequently thus is the law of their order confirmed.
We can recognize order in
two manners. When the law which is the reason
is known to us, it is sufficient to examine whether
the object under consideration satisfies it.
But if we lack this data, it is necessary to seek
to discover, in the organization of the parts of the
object, the law which governs their arrangement;
the recognized law, the order, will be the consequence.
The clock quoted previously offers an example of
the first case: the goal or the law of the provision
of the parts is known there, it is the indication of
time. Thus, when we examine a clock, we have
only to check if its construction answers this goal.
But if we have to consider, for example, the series
of numbers 1, 2, 3, 5, 8, 13, 21, etc, without knowing
which is the law of their increase, the comparison of
these numbers makes us soon discover that each
one is the sum of both which precede it; we
consequently know the law of formation of the series,
i.e., we know the order which reigns there.
It remains to determine of what consists the order of sounds.
It is primarily of two types: according to what is called today
the height or pitch
(low or high), or according to the duration.
One could also speak about order according to the intensity,
but this order is not very quantifiable and rather random,
since a composer can indicate only in a vague way the intensity
of the sounds.
And finally, recognizing preeminence of height
over that of the duration, since that one is measured by the
frequencies
of vibration, Euler brings back the evaluation of the musical pleasure
to the arithmetic measurement of the proportions attached to the sounds.
This 'metaphysics' of music is not completely new.
The 'result' of Eulerian metaphysics is found already in Antiquity
with the Greeks, who had based musical science on the theory of the
proportions (cf. the Division of the Canon of the Euclidean school).
In the same way, the idea that the music consists of the indirect
(or more precisely unconscious) perception of the
ratios of the
sound frequencies is stated by Leibniz:
"musica est exercitium arithmeticae occultum
nescientis se numerare animi."6
But, in spite of these identical themes,
the differences should be stressed which mark the originality
of Euler. Initially, as one will soon be able to judge,
the theory of our mathematician exceeds by far the simple
consideration of the ratios of the frequencies of
two sounds. Then, contrary to his predecessors, who had also
founded their theory on the proportions without any
explanation, Euler outlines a philosophical argumentation,
in which by the proportions one arrives at the musical pleasure,
via the order and the perfection. As for the Leibniz source,
one can undoubtedly recognize from it the influence in the
distinction which Euler makes between the two modes of
perception of the order. But it will be noted that, contrary
to the Master of Hannover, he does not venture to speak
about unconscious perception; perhaps he does not admit the
concept of it, or well, quite simply, he prefers to apply its
engineering to develop mathematical calculations rather than
philosophical considerations.
That said, let us examine how Euler evaluates the order of the
sounds according to their height. By the intermediary of the
vibrations of the air, the musical instruments produce regular
blows or shocks [ictus] on our tympanum. With a preoccupation
for clarity, Euler visualizes these blows, in the case
of the simplest chords of two sounds, by the following figures:
- Bailhache/Monzo]
["'Let us contemplate as an example the mechanism of a clock,
whose goal is to show the parts and divisions of time:
it gives us maximum pleasure, if out of that structure we comprehend
how all the parts are intertwined with each other,
and how their actions all converge to indicate the exact time.
"Ex hisce sequitur, in qua re insit perfectio,
in eadem ordinem necessario inesse debere." [OO, 3a, I, 225]
From this it follows, in that which incorporates perfection,
likewise to order must it necessarily be indebted"
- Monzo]
T2
Thus, in any thing where
there is perfection, there is necessarily also order.
- Bailhache]
"Posterior modus percipiendi ordinis ad musicam praecipue
spectat" [OO, 3a, I, 226]
The second manner of recognizing order is present especially in music."
- Monzo]
The second manner of recognizing order is present especially in music."
- Bailhache]
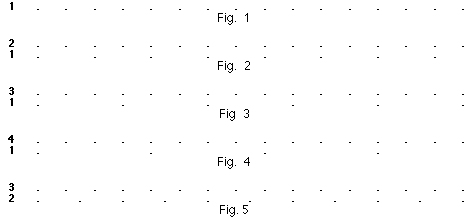
etc...[OO, 3a, I, 231]
This is the place to say some words on the French translation of 1839, since as well the principal topic of our conference is that of the scientific translation. I will be satisfied at a glance on the second chapter, "De suavitate et principiis harmoniae", translated by "On the charms and principles of the harmony". The suavitas will be discussed throughout the work, because one of the major goals that Euler proposes to reach is that to define a scale of "kindness" of the sound aggregates, which he names "suavitatis gradus", "degrees of softness".T4 Useless to notice, under these conditions, that the term of "charm" is not very well selected. Wrote Euler:
"Duobus sonis propositis percipiemus eorum relationem, si intelligamus rationem, quam pulsuum eodem tempore editorum numeri inter se habent; ut si alter eodem tempore 3 pulsus perficiat, dum alter 2, eorum relationem adeoque ordinem cognoscimus observantes hanc ipsam rationem sesquialteram. Similique modo plurium sonorum mutuam relationem comprehendimus, si omnes rationes, quas singulorum sonorum numeri vibrationum eodem tempore editarum inter se tenent, cognoscemus." [OO, 3a, I, 228]
which means [in French]:
"Two sounds being given, we will know the relation which exists between them, if we can grasp the ratio of the number of vibrations carried out for one, with the number of vibrations carried out for the other in the same time. For example, if there were 3 vibrations for the first, while for the second there would be 2 of them, we know their relation and consequently their order, by observing the ratio of the numbers 3 and 2 which is 3:2." [ OCF, 5, 27 ] 7
We see initially that "pulsus" is rendered by "number of vibrations", which corresponds obviously to a desire of modernization of the theory. Literally "pulsus" is an impulse, a shock, and the concept that Euler keeps in mind is certainly that of the shocks (tiny and fast) that the sound bodies produce on the tympanum of the ear by the intermediary of the medium which transmits the sound. In fact, as I explain further on, Euler takes again what one calls now the theory of the coincidence of blows. However, in the following sentence, Euler himself speaks about "numeri vibrationum", which justifies to a certain extent the step of the translator.
We note then that "rationem sesquialteram" is quite simply translated by "3:2". It is again about a modernization, because the sesquialter proportion indicates in Euclid (which Euler takes as a starting point here at least for the terminology) any ratio of the form 1 + 1/n, therefore 3/2 for n = 2.
Let us throw a last glance on the following paragraph:
"Magnum quidem extat in sonorum rationibus percipiendis subsidium, quod singulorum plures ictus percipimus saepiusque eos inter se comparare possumus. Idcirco multo est facilius duorum sonorum rationem discernere audiendo quam duarum linearum eandem rationem habentium intuendo." [OO, 3a, I, 228]
[in French:]
"The appreciation of the relationship between the sounds, is singularly facilitated by this circumstance whereby we perceive several vibrations of each one, and whereby thus we can, for their length of time, compare them several times one with the other. It is thus much easier to distinguish by hearing the ratio of two sounds, than to recognize by the [sense of] sight the same relationship between two lines." [ OCF, 5, 27-28 ]