Reply-To: jhchalmers@ucsd.edu
To: Joe Monzo
Subject: Your 3 messages
Date: Thu, 08 Apr 1999 10:35:51 +0000
NCP means New Chalmers Plot, but I suppose I should call it something like DPMP, for Doubly Proportional Monzo Plot.
Discard the lattices I sent you the day before yesterday (or whenever, I sent youy a correction message) as I had a bug in the program. I solved it by taking the absolute value of the arctangent of the y/x coordinates when I computed the angles the interval radius vectors make with the virtual axes. I realize this sound like gibberish, but the latest plots require a lot of trig. Were I Graeme what's his name, I'd use matrices rather than explicit BASIC commands, but it'd take me too long to refresh my memory of linear algebra and write the new code.
Since late 1995, I've written a long series of latticing programs, though I haven't updated all of them for color yet. Beginning with rectilinear lattices for 3, 5 and 7, I implemented 11-17. After some email with Erlich who used tetrahedral lattices for 3, 5, and 7, I realised that these are the same as Wilson's centered triangular lattices. So I did these and quickly expanded my program to higher polygons, ending with a centered 13-agon. However, these later programs severly test MS's BASIC system and the programs wouldn't always run or compile. When the did, I captured B&W pix for transparencies for talks I've given.
I also started implementing your plots, first by taking measurements from your diagrams, secondly by computing the angles of axes as you specified.
Then I decided to try incorporate interval width information into the plots, but did so in stages. First I made the axes unit proportional to the cents of the prime factors (in one octave). Then I converted the axis units so that both the harmonic and subharmonic axis intervals were proportional to the cents of the otonal and utonal ratios. Thus the notes defined by sub-3's are depicted by a smaller axis unit (becaue 4/3 < 3/2) than those defined by 3's.
However, though it was easy to define the axes (powers and sub-powers of 3, 5 and 7), composites such as 15/8 and 5/3 were difficult. The distances from 1/1 could be specified as the sum or differences of the prime ratios (or their inversions) - in practice, I worked from the cents of the ratio directly; the corresponding angles are less well defined.
What I did for the angles was to calculate the positions of the notes on a proportional lattice, derive x and y coordinates from it, and from these coordinates define the angle theta as the arctangent of the ratio y/x. Then I used this theta and the cents-proportional radius vector to locate each note. Finally, after connecting harmonic nearest-neighbors (notes differing by only 1 step along any prime axis), I added the 12-tet circles to show the interval sizes in cents.
Since I have to use a cartesian x-y system to plot points anyway, I first made proportional plots for the rectangular system (called PRP, though it should be NCP, I think). Once I got this working, I made the conversion to the Monzo plot where the angles are proportional to the cents of the prime factors.
I think everything is working now. Whether these plots are comprehensible or not is an open question. There is no reason why one couldn't extend these to higher prime factors, but whether it's worth the trouble, I don't know yet.
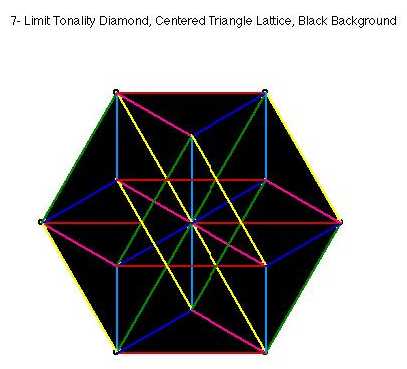
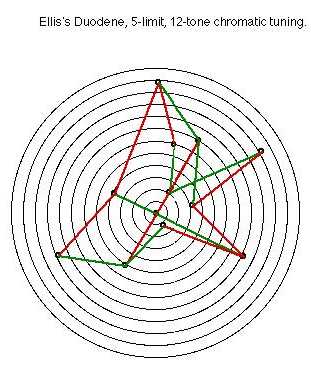
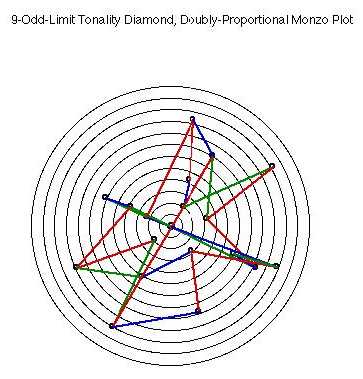
These attachments: new Duodene and 9 limit diamond plots and a black background version of the 7 limit diamond triangular plot.
--John Attachment: 9oddlimitdiamondDPMP Attachment: DuodeneDPMP Attachment: Blackbckgrd7diamondTL
7-Limit Diamond - Centered Triangular (Wilson/Erlich)
Ellis 5-Limit Duodene - Doubly Proportional Monzo Plot
9-Odd-Limit Diamond - Doubly Proportional Monzo Plot
created 1999-4-8
|
or try some definitions. |