Message: 26
Mandelbaum and/or Würschmidt call 128:125 the "major
diesis,"
contradicting Keenan's recent definitions. Is there an accepted
convention on this? Manuel?
In his appendix to Helmholtz [in the 'Table of Intervals
not exceeding one
Octave'], Ellis lists 125:128 as the...
Great Diesis, the defect of 3
major Thirds from an Octave,
the
interval
between C# and Db in the
meantone
temperament,
3Td = C2# : D1b, ex.[= exact
cents] 43.831
I happen to have missed Dave's definition of intervals,
but apparently they don't conform exactly to those I'm
familiar with.
Dave, Paul, and anyone else who needs to discuss intervals
should have available Helmholtz 1885
and Rameau 1971. Ellis
and Rameau give names to intervals that have pretty much
been adopted by theorists as the standard ones, at least for
'common-practice'
harmony.
I'll try to give you a sense of why meantone (and thus
Vicentino's
JI scheme) works for anything in the Western
repertoire without
enharmonic respellings, and what happens
when you do have enharmonic respellings. Basically, there are
only two independent
commas that come into play when trying
to analyze or render music of the Western conservatory
tradition in
just intonation.
Let's take the
syntonic comma
and the
Pythagorean comma
as the two basic ones (any two would
do). The syntonic comma is four
fifths minus a third, so we can
write it as s=4v-t. The Pythagorean comma is twelve fifths;
write it as p=12v. Other important commas:
1. schisma = -8v-t = s-p
If you think there might be others, check out Mathieu's
_Harmonic Experience_, which is a thorough survey of Western
harmony through JI glasses. Mathieu does not mention the
"major diesis" but he does name one other, the "superdiesis",
which is 8v-2t = 2*s. But basically, we've got it all covered.
Structurally, the syntonic comma results in no notational
change, while the Pythagorean comma changes a flat to the
enharmonic sharp (e.g., Ab->G#). (You may want to verify this
for yourself). From the equations above, we can see that commas
1-4 above all result in a notational change opposite that of
the Pythagorean comma, i.e. they change a sharp to the
enharmonic flat.
[Paul's equations are illustrated on the lattice below.
Note that the first one should really be schisma
= 8v+t = p-s , so that the skhisma also acts like the
Pythagorean comma, changing a flat to the enharmonic sharp.]
From the 'practical' point of view of "trying
to analyze or render music of the Western conservatory
tradition in
just intonation", Paul is probably right that
these 'commas' (the smallest and largest of which are actually
forms of skhisma and diesis, respectively) are the only ones
that need be considered.
But strictly speaking, depending on how far one takes the
powers of 3 and 5 in any given 2-dimensional
lattice or
periodicity-block,
there are all sorts of 'commas' that may
come into play.
Paul is using 'comma' here in a very generic sense to mean
a small interval, which in many cases will be used as a
unison vector
to delimit the boundaries of a periodicity-block.
Wilkinson 1988
uses the term '
anomaly' as a generic word
designating several different of these: skhismas, commas,
and dieses, and I use it too.
I've made a lattice diagram giving the cents-values of all
the 5-limit intervals between 0 and 100 cents, within the
arbitrary exponent-limits of +/-15 for
prime-base 3 and
+/-7 for prime-base 5. Hopefully some of you will find this
useful.
In addition to the 'anomalies', this lattice also indicates
the smaller of the 5-limit
'semitones'.
It can be seen easily from the lattice that these intervals, as well
as some lesser-known 'commas' like 243:250 and 3072:3125, cannot made
up of various combinations of the ones described by Paul.
Western triadic music prior to Beethoven requires
"bridging" solely
through the
syntonic comma,
and hence is often performed in
meantone
temperament. Since Beethoven, "bridging" through syntonic comma and
*any* (and therefore, all) of the other 'commas' paul mentions above
(in connection with Mathieu) has been a feature of western
triadic
music, hence the use of
12-tone equal
(or well) temperament. The
other 'commas' can be used for bridging in other, "invented" musical
systems, motivating certain corresponding tuning systems as shown in
the "Equal Temperament"
entry. For example, you can see from the first chart and table on that page
that "bridging" through 243:250 is characteristic of porcupine
temperament, through 3072:3125 of magic temperament, and through both
of them (and thus also any combination of the two) of 22-tone equal
temperament.
The lattice also makes it easy to see the
periodicity
inherent in the system, as the patterns of relationship between
several small intervals repeats at several places in the lattice.
Below is a table giving the intervals listed by Erlich and
by Ellis. (Edited, and incorporating additions
I made in TD 484.1, giving Rameau's interval-names.)
My lattice shows many more, the names of which I
don't know.
Scala
probably gives them. ...? If not,
perhaps I can provide some new names. Manuel?
Here are some suggestions for a logical system encompassing
more 'commas' than most other systems. It classifies
intervals into seven broad groups (from smallest to largest):
skhisma,
kleisma,
comma,
small diesis, great diesis,
small semitone, and
limma.
Each interval is qualified by a pseudo-Graeco-Latin term
indicating the exponent of 5 and its 'tivity', positive
or negative. (Is there a real mathematical term for that?)
I don't particularly like these names, but the set of
these intervals in this lattice fell roughly into 11 groups
(based on the gaps in the graph of their cents-values),
which I condensed into these seven groups:
Date: Tue, 11 Jan 2000 03:16:13 -0500
From: Joe Monzo
Subject: 5-limit intervals, 100 cents and under
[Paul Erlich, TD 479.23]
[Ellis in Helmholtz 1885, p 453]
[Paul Erlich, TD 477.10]
2. diaschisma = -4v-2t = 2*s-p
3. (minor or Great) diesis = -3t = 3*s-p
4. major diesis = 4v-4t = 4*s-p
power of 5
2 1 0 -1 -2 -3 -4 -5
15 --- --- --- --- --- --- --- ---
| | | | | | | |
14 --- --- --- --- --- --- --- ---
| | | | | | | |
13 --- --- --- --- --- --- --- ---
| | | | | | | |
12 --- --- Pythagorean--- --- --- ---
| | comma | | | | |
11 --- --- --- --- --- --- --- ---
| | | | | | | |
10 --- --- --- --- --- --- --- ---
p | | | | | | | |
o 9 --- --- --- --- --- --- --- ---
w | | | | | | | |
e 8 --- skhisma --- --super-- --- ---
r | | | | diesis | | |
7 --- --- --- --- --- --- --- ---
o | | | | | | | |
f 6 --- --- --- --- --- --- --- ---
| | | | | | | |
3 5 --- --- --- --- --- --- --- ---
| | | | | | | |
4 --- --- --- syntonic --- -major--
| | | comma | | diesis |
3 --- --- --- --- --- --- --- ---
| | | | | | | |
2 --- --- --- --- --- --- --- ---
| | | | | | | |
1 --- --- --- --- --- --- --- ---
| | | | | | | |
0 --- --- [origin] --- -great-- ---
| | | | | diesis | |
-1 --- --- --- --- --- --- --- ---
| | | | | | | |
-2 --- --- --- --- --- --- --- ---
| | | | | | | |
-3 --- --- --- --- --- --- --- ---
| | | | | | | |
-4 --- --- --- -- diaschisma --- ---
[commentary from Paul Erlich:]
Lattice of cents-values of 5-limit intervals from 0 to 100 cents
with arbitrary boundaries of 3^-15...15 * 5^-7...7
by Joe Monzo 2000.1.11
----------------------------------------------------------------
power of 5
7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7
15 34--- --- ---75--- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
14 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
13 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
12 --- --- --- --- --- --- ---23--- --- ---65--- --- --- ---
| | | | | | | | | | | | | | |
11 --- ---53--- --- ---94--- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
10 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
9 --- --- --- --- --- --- --- --- --- --- --- --- --- ---13
| | | | | | | | | | | | | | |
8 --- --- --- --- --- --- 2--- --- ---43--- --- ---84--- ---
| | | | | | | | | | | | | | |
7 ---32--- --- ---73--- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
6 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
5 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
4 --- --- --- --- --- --- --- ---22--- --- ---63--- --- ---
| | | | | | | | | | | | | | |
3 10 --- --- ---51--- --- ---92--- --- --- --- --- --- --- ---
p | | | | | | | | | | | | | | |
o 2 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
w | | | | | | | | | | | | | | |
e 1 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
r | | | | | | | | | | | | | | |
0 --- --- --- --- --- --- --- 0--- --- ---41--- --- ---82 ---
o | | | | | | | | | | | | | | |
f -1 --- ---30--- --- ---71--- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
3 -2 100--- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-3 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-4 --- --- --- --- --- --- --- --- ---20--- --- ---61--- ---
| | | | | | | | | | | | | | |
-5 --- 8--- --- ---49--- --- ---90--- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-6 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-7 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-8 --- --- --- --- --- --- --- --- --- --- ---39--- --- ---80
| | | | | | | | | | | | | | |
-9 --- --- ---28--- --- ---69--- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-10 ---98--- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-11 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-12 --- --- --- --- --- --- --- --- --- ---18--- --- ---59 ---
| | | | | | | | | | | | | | |
-13 --- --- 6--- --- ---47--- --- ---88--- --- --- --- --- ---
| | | | | | | | | | | | | | |
-14 77 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-15 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
~cents ratio prime-factor name
3^ 5^ Ellis Rameau
92 128:135 | 3 1 | larger limma mean semitone
90 243:256 |-5 0 | pythagorean limma
71 24:25 |-1 2 | small semitone minor semitone (theory), aug. unison (practice)
63 625:648 | 4 -4 | (Erlich 'major diesis') least semitone
49 243:250 |-5 3 | major diesis
43 6400:6561 | 8 -2 | (Mathieu 'superdiesis')
41 125:128 | 0 -3 | great deisis minor diesis
30 3072:3125 |-1 5 | small diesis
23 524288:531441 |12 0 | pythagorean comma
22 80:81 | 4 -1 | syntonic comma comma
20 2025:2048 |-4 -2 | diaskhisma diminished comma
2 32768:32805 | 8 1 | skhisma
Note that 5^-3 [= 125:128 = ~41 cents] was called 'minor
diesis' by Rameau and 'Great Diesis' by Ellis. (These two
different terms were noted by Paul Erlich in the posting
I quoted.)
Also note that 3^4*5^-4 [= 625:648 = ~63 cents] was called
'least semitone' by Rameau and 'major diesis' by Erlich
(and I presume Keenan).
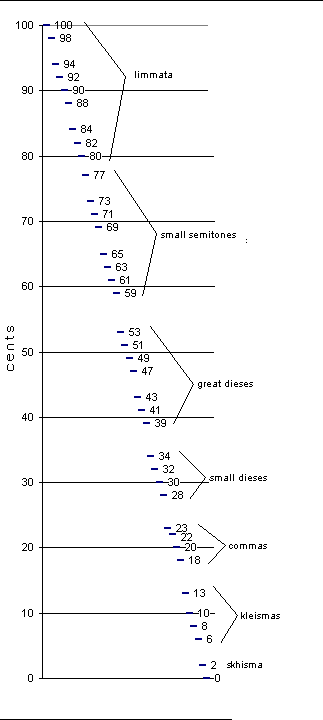
Suggested terminology for 5-limit intervals from 0 to 100 cents
with arbitrary boundaries of 3^-15...15 * 5^-7...7
by Joe Monzo 2000.1.11
----------------------------------------------------------------
~cents ratio prime-factor name proposed by Monzo
3^ 5^
100 73728:78125 |- 2 7 | super-septapental limma
98 59049:62500 |-10 6 | super-hexapental limma
94 4194304:4428675 | 11 2 | super-bipental limma
92 128:135 | 3 1 | super-pental limma (Ellis larger limma, Rameau mean semitone)
90 243:256 |- 5 0 | Pythagorean limma
88 7971615: 8388608 |-13 - 1 | sub-pental limma
84 6250:6561 | 8 - 5 | sub-pentapental limma
82 15625: 16384 | 0 - 6 | sub-hexapental limma
80 512578125:536870912 |- 8 - 7 | sub-septapental limma
77 4782969: 5000000 |-14 7 | super-septapental small semitone
73 262144:273375 | 7 3 | super-tripental small semitone
71 24:25 |- 1 2 | super-bipental small semitone (Ellis small semitone, Rameau minor semitone)
69 19683: 20480 |- 9 1 | super-pental small semitone
65 512000:531441 | 12 - 3 | sub-tripental small semitone
63 625:648 | 4 - 4 | sub-tetrapental small semitone (Erlich major diesis, Rameau least semitone)
61 253125:262144 |- 4 - 5 | sub-pentapental small semitone
59 8303765625:8589934592 |-12 - 6 | sub-hexapental small semitone
53 536870912:553584375 | 11 5 | super-pentapental great diesis
51 16384:16875 | 3 4 | super-tetrapental great diesis
49 243:250 |- 5 3 | super-tripental great diesis (Rameau major diesis)
47 1594323:1638400 |-13 2 | super-bipental great diesis
43 6400:6561 | 8 - 2 | sub-bipental great diesis (Mathieu superdiesis)
41 125:128 | 0 - 3 | sub-tripental diesis (Ellis great diesis, Rameau minor diesis)
39 4100625:4194304 |- 8 - 4 | sub-tetrapental great diesis
34 1099511627776:1121008359375 | 15 7 | super-septapental small diesis
32 33554432:34171875 | 7 6 | super-hexapental small diesis
30 3072:3125 |- 1 5 | super-pentapental small diesis (Ellis small diesis)
28 19683:20000 |- 9 4 | super-tetrapental small diesis
23 524288:531441 | 12 0 | Pythagorean comma
22 80:81 | 4 - 1 | sub-pental comma (syntonic comma, Rameau comma)
20 2025:2048 |- 4 - 2 | sub-bipental comma (Ellis diaskhisma, Rameau diminished comma)
18 66430125:67108864 |-12 - 3 | sub-tripental comma
13 78125: 78732 | 9 - 7 | sub-septapental kleisma
10 2097152:2109375 | 3 7 | super-septapental kleisma
8 15552:15625 |- 5 6 | super-hexapental kleisma (Tanaka kleisma)
6 1594323:1600000 |-13 5 | super-pentapental kleisma
2 32768:32805 | 8 1 | super-pental skhisma (Ellis skhisma)
0 1:1 | 0 0 | reference pitch
Lattice of proposed names of 5-limit intervals from 0 to 100 cents
with arbitrary boundaries of 3^-15...15 * 5^-7...7
by Joe Monzo 2000.1.11
----------------------------------------------------------------
power of 5
7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7
15 sm diesis -- sm s-t.- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
14 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
13 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
12 --- --- --- --- --- --- -comma-- --- sm s-t.- --- --- ---
| | | | | | | | | | | | | | |
11 --- lg diesis --- limma -- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
10 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
9 --- --- --- --- --- --- --- --- --- --- --- --- --- kleisma
| | | | | | | | | | | | | | |
8 --- --- --- --- --- schisma- --- lg diesis --- limma -- ---
| | | | | | | | | | | | | | |
7 sm diesis --- sm s-t.- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
6 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
5 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
4 --- --- --- --- --- --- --- -comma-- --- sm s-t.- --- ---
| | | | | | | | | | | | | | |
3 kleisma --- lg diesis --- limma -- --- --- --- --- --- --- ---
p | | | | | | | | | | | | | | |
o 2 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
w | | | | | | | | | | | | | | |
e 1 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
r | | | | | | | | | | | | | | |
0 --- --- --- --- --- --- - 1/1 -- --- lg diesis --- limma --
o | | | | | | | | | | | | | | |
f -1 --- sm diesis --- sm s-t.- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
3 -2 100--- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-3 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-4 --- --- --- --- --- --- --- --- -comma-- --- sm s-t.- ---
| | | | | | | | | | | | | | |
-5 kleisma- --- lg diesis --- limma -- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-6 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-7 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-8 --- --- --- --- --- --- --- --- --- --- lg diesis --- -limma
| | | | | | | | | | | | | | |
-9 --- --- sm diesis --- sm s-t.- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-10 ---98--- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-11 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-12 --- --- --- --- --- --- --- --- --- -comma-- --- sm s-t.-
| | | | | | | | | | | | | | |
-13 --- kleisma- --- lg diesis --- limma -- --- --- --- --- ---
| | | | | | | | | | | | | | |
-14 sm semi --- --- --- --- --- --- --- --- --- --- --- --- ---
| | | | | | | | | | | | | | |
-15 --- --- --- --- --- --- --- --- --- --- --- --- --- ---
REFERENCES
----------
Helmholtz, Hermann. 1885.
_On the Sensations of Tone as a Physiological Basis
for the Theory of Music_.
English translation by Alexander J. Ellis, of
_Die Lehre von den Tonempfindungen..._, Braunschweig, 1863.
2nd edition, conforming to 4th German edition (1877).
Reprint: 1954, Dover Publications, New York.
ISBN# 0-486-60753-4
(back to text)
Rameau, Jean-Philippe. 1971.
_Treatise on Harmony_.
English translation by Philip Gossett, of
_Traite' de l'harmonie_, Paris, 1722.
Dover Publications, New York.
ISBN# 0-486-22461-9
(back to text)
Wilkinson, Scott R. 1988.
_Tuning In: Microtonality in Electronic Music_.
Hal Leonard Books, Milwaukee.
(back to text)
-monz
Joseph L. Monzo Philadelphia monz@juno.com
http://www.ixpres.com/interval/monzo/homepage.html
|"...I had broken thru the lattice barrier..."|
| - Erv Wilson |
--------------------------------------------------