en français

Deutsche

De Joe Monzo

Diagramas Harmonicas “Lattice”

Texto e diagramas © 1998 por Joseph L. Monzo

 

 

A melhor maneira que eu descobri, de extrair tanta informação harmônica de um sistema de afinação de entonação justa quanto possível, é o uso de diagramas “lattice” as quais retratam alturas como pontos no espaço multi-dimensional conectado por vetores.

Em um sistema de afinação de entonação justa, cada nota é  representada por uma razão a qual descreve a relação daquela nota com outra, normalmente com uma nota que é usada como referência para todo o sistema. Esse tom de referência tem a razão de 1/1, também escrita como 1:1, or 1 para 1.

Qualquer número pode ser fatorizado? em uma série de números primos, cada qual é uma base que tem um expoente que é tanto positivo como negativo, representando números > 1 ou < 1, respectivamente, a não ser que o expoente seja igual a 0, o que representa 1, a identidade na multiplicação.

Potências de 2 são todas harmonicamente equivalentes a essa identidade 1, sendo assim, potências de 2 representam “oitavas”, o que tem nenhum efeito pronunciado na harmonia, e podem ser eliminadas, a não ser que registro de “oitava” esteja sendo especificamente levada em consideração. Dessa maneira os diagramas normalmente começam com a base de número primo 3.

 

Meus diagramas de “lattice” tratam cada base primária com uma dimensão única no espaço, com todos os expoentes “radiando” em volta do centro 1/1, o que é equivalente a todos os números elevados à 0° potencia, ou n°.

Consideradas em um espaço bi-dimensional, os vetores que conectam cada exponencial percorrem em uma direção única para cada primo. Essa direção é determinada pelo ângulo que representa os valores em “cents” (dentro da “oitava”) daquele primo elevado à primeira potência, começado da posição de 6 horas do relógio.

 

Sendo assim, 3¹, que é a razão de 3/2 e tem o valor em cents de  702, tem um vetor “radiando” de 1/1 em uma posição bem próxima de 1 hora ( porque 6 + 7 mod 12 = 1).

5¹, que é a razão de 5/4 e tem o valor em cents de 386, tem um vetor “radiando” logo antes da posição de 10 horas ( 6 + 3.86 = 9.86), e assim por diante.

Os exponentes negativos simplesmente radiam para fora de uma posição oposta.

Os vetores também variam em tamanho e grossura de acordo com as bases de número-primo que estão se conectando, sendo 3 a mais fina e mais grossa.

 Curiosamente, mesmo que o espaço bi-dimensional seja o “mileu?” em que essas medidas foram feitas, elas se mostram aos olhos na forma estrutural de 3 ou mais dimensões, de certo modo se assemelhando a cristais.

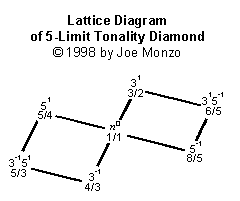
Harry Partch inventou uma estrutura a qual ele chamou de "Tonality Diamond" (Diamante da Tonalidade). O diamante mostra todas as relações harmônicas das razões com números inferiores a um certo “Limite Ímpar” (excluindo o “dobramento da oitava”, ou multiplicação por 2, a qual ele usava para manter cada razão dentro da mesma “oitava”, como na maioria das fontes de escalas comuns).

Esse “Diamantes”, que simplesmente ficam maiores e mantêm exponencialmente mais razões com cada novo Limite-Ímpar acima na versão de Partch, se apropriam de um aspecto completamente diferente quando ilustrados pelo uso das minhas “LATTICES”. O processo certamente apela às minhas sensibilidades artísticas.

Aqui eu ilustro os “Diamantes da Tonalidade” com Limite-5, Limite-7, Limite-9, Limite-11, e Limite-13, representados pelos meus diagramas de “LATTICES”.

A simetria que Partch percebeu em suas escalas e Diamantes de Tonalidades são rapidamente evidentes aqui, embora os Diamantes da Tonalidade em sua representação não sejam perfeitamente simétricos, como são outros sistemas que eu revisei.

 

Partch chamava isso de Diamante da Tonalidade Incipiente, porque a tríade com as proporções 4:5:6 nos dão a consonância máxima para um acorde com três identidades distintas, portanto este é o sistema mais simples que pode ser construído o qual pode nos dar algum sentimento verdadeiro da tonalidade.

A tríade “maior” são assim representadas pela minha “LATTICE” (odentidades dadas):

 

 

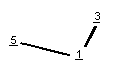
Tríade menor (com udentidades):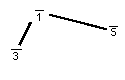

 

Percebam que a “LATTICE” de Limite-5 ou o Diamante contêm 3 de cada tríade “menor” e “maior”. Cada sistema de Limite- n sempre contêm (n +1) acordes de consonância máxima, cada um com (n+1)/2 identidades, distribuídas igualmente dentro de (n+1)/2 de cada tríade “maior” e “menor”

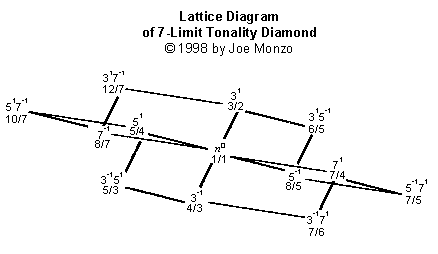
Percebam que a LATTICE de Limite-9 não tem uma nova dimensão, apenas uma camada é adicionada, em cada extremidade das potências de 3, da LATTICE de Limite-7. Isso se explica pelo fato que 9 não é um número primo, mas sim um composto, ou seja, um número formado por outros números primos, nesse case 3 x 3, ou 3².

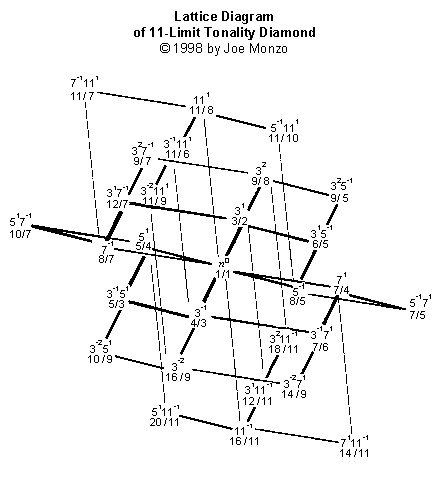
Esta é uma versão da LATTICE de Limite-11 em cores completas:

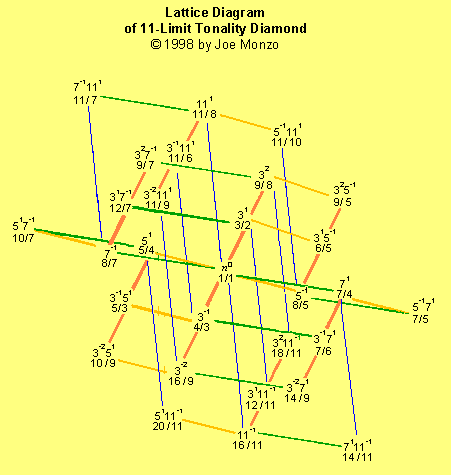
(Esta aqui pode aparentar melhor em seu sitema, mas demora um pouco para carregar.)

A próxima é um versão sombreada da LATTICE de Limite-11 a qual é a minha favorita:

 

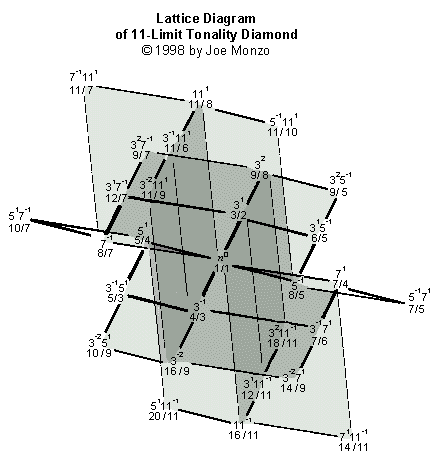
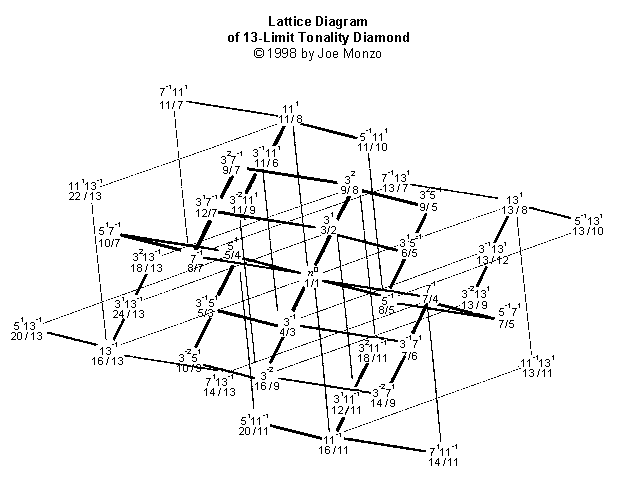
E o set mais complicado de todos, a LATTICE de Limite-13:

 

As LATTICES formam estruturas intricadas que se parecem com cristais que mostram a riqueza da informação harmônica em apenas um olhar. Se forem vistas na ordem listada acima, podemos ver que cada diagrama menor é contido dentro dos maiores.

Abaixo temos uma LATTICE usando minhas convenções comuns, exceto que o ângulo de cada eixo-primo é o “ângulo dourado” de ~222.49 graus, e a largura de cada passo em cada eixo é Log(primo). A idéia foi sugerida por Paul Erlich (Yahoo tuning list message 22065 Thu May 3, 2001 2:38 pm):

Seria uma idéia de espelhar a forma que muitas plantas e flores crescem. Primeiro, um primeiro

The idea would be to mirror the way many plants and flowers grow. First, a single "bud" pops out of the center. After the first bud has grown a bit, the next "bud" pops out at the golden angle (222.49 degrees). Then the next bud pops out at the golden angle relative to that. And so on. Each bud would represent a different prime. This would ensure that, if you used a lot of different primes in your lattice, their lines would stay as far as possible from one another and near-overlaps would be avoided.

Esse é o mapeamento Básico dos primos na LATTICE:

E este, como um exemplo, é o Diamante da Tonalidade de Limite-11:

·  Para mais diagramas e explicações de afinações históricas, vejam meu livro ·  Se você não entende a minha teoria ou os termos que usei,  comece aqui ou tente algumas definições.

Aceito sugestões sobre este website: correções, melhorias, bons links. Me diga se você não entendeu alguma coisa. retornar para minha home page  retornar para Sonic Arts home page