Neumann was incorrect when he said:
"... As intermediate stages between the 12 and the 53-part division of the octave only multiples of 12 could be considered, thus, division into 24, 36, and 48 parts; for with any other number of parts there would be no sufficiently pure fifth." [emphasis Monzo]
There are, in fact, two equal-temperaments smaller than 53edo which do give better approximations to the "5th" than 12edo or its multiples:
29edo
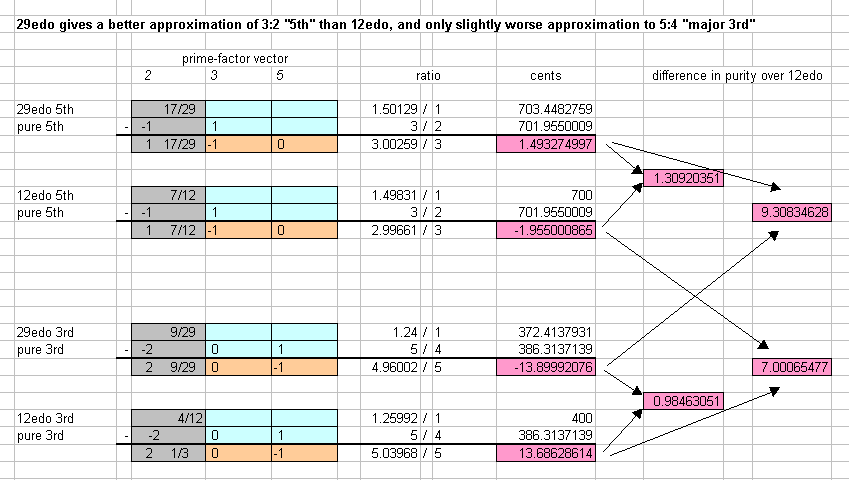
In the above diagram, it can be seen that 29edo gives an approximation to the 3:2 "5th" that is about 11/3 times "purer" than that of 12edo, and that the 29edo approximation to the 5:4 "major 3rd" is only very slightly worse than that of 12edo.
Because the improvement in the approximation to the "5th" is so small, and also because the approximation to the "3rd" is actually a bit worse, i'm not too surprised that Neumann disregarded 29edo. But 41edo is a different story...
41edo
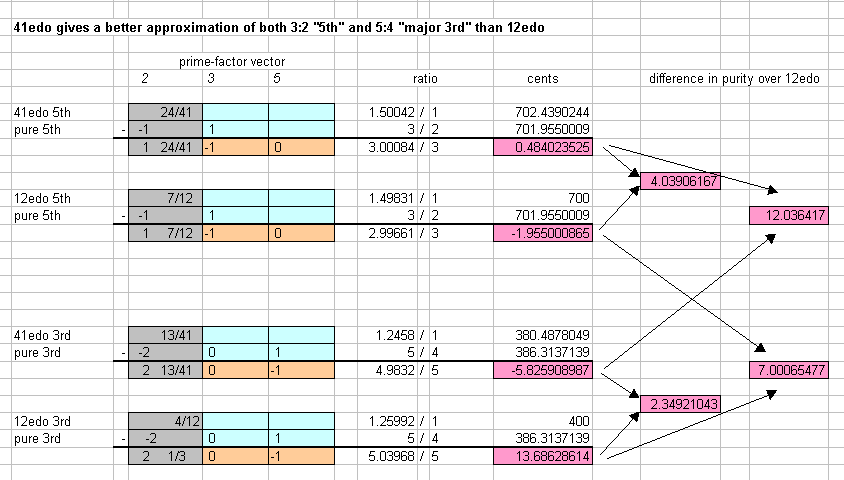
In the above diagram, it can be seen that 41edo gives an approximation to the 3:2 "5th" that is about 4 times "purer" than that of 12edo, and that the 41edo approximation to the 5:4 "major 3rd" is about 21/3 times "purer" than that of 12edo.
Here we have a significant improvement over 12edo and its multiples for both of these important intervals. Admittedly, it is nowhere near as impressive as the ~282/3 times "purer" "5th" and ~93/4 times "purer" "3rd" of 53edo (see my analysis), but still ... it's remarkable to me that Neumann would go to such trouble to present this mathematical comparison and commit such a blatant error.