Our major scale,
the series of tones c, d, e, f, g, a, b,
the tones that also provided the basis for the Greek and church modes,
we can explain as having been found through imitation of nature.
Intuition and inference assisted
in translating
the most important characteristic of the tone, the overtone series,
from
the vertical (as we imagine the position of all simultaneous sounds)
into
the horizontal, into
separate, successive tones.
The natural model, the tone, exhibits the following characteristics:
1. A musical sound is a composite,
made up of a series of tones sounding together, the overtones;
hence, it forms a chord.
From a fundamental, C, these overtones are:
|
etc. |
|
|
C |
c |
g |
c 1 |
e 1 |
g 1 |
(b b1) |
c 2 |
d 2 |
e 2 |
f 2 |
g 2 |
|
|
overtone |
Fundamental |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
partial |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
prime factor |
n 0 |
n 0 |
31 |
n 0 |
51 |
31 |
71 |
n 0 |
32 |
51 |
111 |
31 |
|
111 |
||||
|
F |
||||
|
71 |
||||
|
B b |
||||
|
(7... n)0 |
E |
|||
|
C |
G |
D |
2. In this series the c is the strongest sound because
- it occurs the greatest number of times, and because
- it is actually played or sung itself, as a fundamental.
3. After the c
the next strongest tone is g, because
- it occurs earlier in the series, therefore
- more often than the other tones.
If we think of this g as a real tone
(as indeed occurs when the overtone series is realized horizontally,
when, for example, the 5th of a horn tuned in c is played),
it then has overtones itself (as a tone actually played); these are:
|
etc. |
|
|
g |
g 1 |
d 2 |
g 2 |
b 2 |
d 3 |
etc. |
|
|
overtone |
fundamental |
1 |
2 |
3 |
4 |
5 |
|
|
partial |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
prime factor |
31 |
31 |
32 |
31 |
3151 |
32 |
|
(7... n)0 |
E |
B |
||
|
C |
G |
D |
and at the same time
this g, together with its overtones,
presupposes the C (fundamental of the horn).
Thus it happens that
the overtones of the overtones also contribute to the total sound.
dependent upon a tone a 5th below, the C.
The conclusion that follows from the foregoing:
This tone, C, is likewise dependent upon the tone a 5th below it, F.
[p 22]
Now if the C is taken as the midpoint, then
its situation can be described by reference to two forces:
- one of which pulls downward, toward F1,
- the other upward, toward G:
G ^ C v F
Here the dependence of G on C,
with which, strictly speaking,
the force of the C is exerted in the same direction as that of the F,
may be considered like
the force of a man
- hanging by his hands from a beam and
- exerting his own force against the force of gravity.
He
- pulls on the beam just as
- gravity pulls him,
and in the same direction.
[Carter, p 24:]
But the effect is that
- his force works against the force of gravity,
and so in this way
one is justified in speaking of the two opposing forces.
I will
- often speak of this characteristic and will
- draw a number of conclusions from it.
What is important for the moment is
to establish that
- these tones are very closely related to one another, that
- they are next of kin.
G is the first overtone (after c) of C, and
c the first of F.
Such an overtone
- bears the closest similarity to the fundamental
(after the octave), therefore
- contributes most to
- the quality of the sound, to
- its euphony.
If
one is justified in assuming that
the overtones of the G can become real tones,
then
this assumption may be applied analogously to those of F.
After all,
F is to C as
C is to G.
And thus it is explained how
the scale that finally emerged is put together from
the most important components of
a fundamental tone and its nearest relatives.
These nearest relatives are
just what gives the fundamental tone stability; for
it represents the point of balance
between their opposing tendencies.
This scale appears as
- the residue of the properties of the three factors, as
- a vertical projection, as
- addition:
|
F |
f |
c 1 |
f 1 |
a 1 |
|||||||||||
|
partial |
1 |
2 |
3 |
4 |
5 |
||||||||||
|
c |
c 1 |
g 1 |
c 2 |
e 2 |
|||||||||||
|
partial |
1 |
2 |
3 |
4 |
5 |
||||||||||
|
g |
g 1 |
d 2 |
g 2 |
b 2 |
|||||||||||
|
partial |
1 |
2 |
3 |
4 |
5 |
||||||||||
|
|
|||||||||||||||
|
F |
c |
f |
g |
c 1 |
f 1 |
g 1 |
a 1 |
c 2 |
d 2 |
e 2 |
g 2 |
b 2 |
|||
|
prime factor |
3-1 |
n 0 |
3-1 |
31 |
n 0 |
3-1 |
31 |
3-151 |
n 0 |
32 |
51 |
31 |
3151 |
||
|
(7... n)0 |
A |
E |
B |
|
|
F |
C |
G |
D |
[p 23]
Adding up the overtones (omitting repetitions) we get the seven tones of our
scale. Here they are not yet arranged consecutively. But even the scalar
order can be obtained if we assume that the further overtones are also in
effect. And that assumption is in fact not optional; we must assume the
presence of the other overtones. The ear could also have defined the relative
pitch of the tones discovered by comparing them with taut strings, which of
course become longer or shorter as the tone is lowered or raised. But the
more distant overtones were also a dependable guide. Adding these we get
the following:
Fundamental Overtones
F f . . . c . . f . a . c . (eb) f g a bb* c etc. f etc.
C c . . . g . . c . e . g . (bb) c d e f etc.
G g . . . d . . g . b . d . (f) g a b c d
----------------------------------------------------------------------------
(eb) (bb)
c d e f g a b c d e f g a b c d
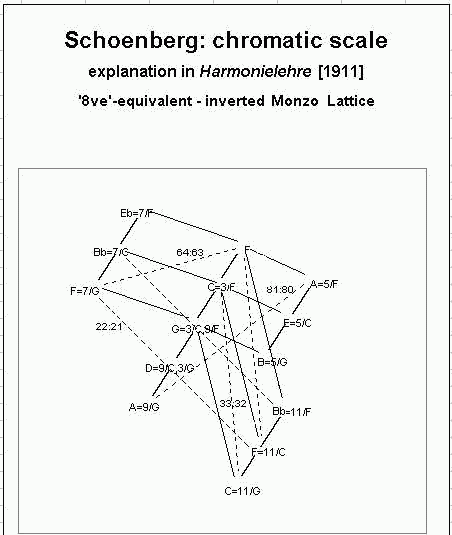
Below is a
lattice diagram
illustrating all of the pitches and relationships in Schönberg's
diagram.]
* [note from Monzo: Carter's 1978 English translation contains a serious error
at this point of this diagram: in the original 1911 German edition the 11th
partial of F is shown as "b", which in German means our B-flat; Carter notates
it as our "b". See the beginning of my analysis of Schoenberg's overtone-theory,
Searching for Schönberg's
Pantonality, for a detailed explanation. Below is an expanded version
of Schönberg's diagram, giving the numerical values of the overtones
which make plain the ratios involved in Schönberg's analysis.
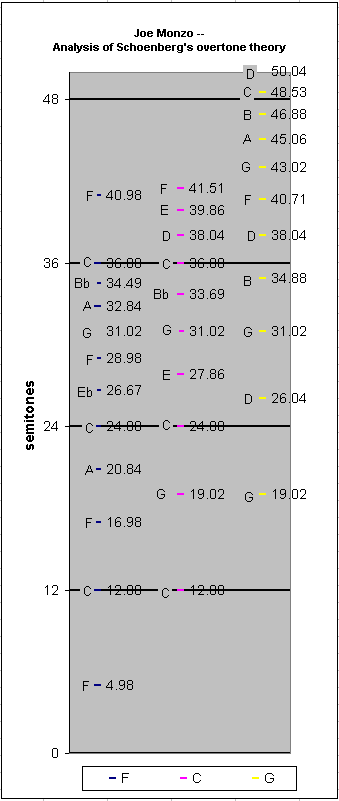
The fundamentals are F = 4, C = 6, G = 9.
d = 12*9 = 108
c = 11*9 = 99
b = 10*9 = 90
a = 9*9 = 81
g = 8*9 = 72
f = 11*6 = 66
f = 16*4 = 64
(f = 7*9 = 63)
e = 10*6 = 60
d = 9*6 = 54 d = 6*9 = 54
c = 12*4 = 48 c = 8*6 = 48
b = 5*9 = 45
bb= 11*4 = 44
(bb= 7*6 = 42)
a = 10*4 = 40
g = 9*4 = 36 g = 6*6 = 36 g = 4*9 = 36
f = 8*4 = 32
e = 5*6 = 30
(eb= 7*4 = 28)
d = 3*9 = 27
c = 6*4 = 24 c = 4*6 = 24
a = 5*4 = 20
g = 3*6 = 18 g = 2*9 = 18
f = 4*4 = 16
c = 3*4 = 12 c = 2*6 = 12
f = 2*4 = 8
arranged as a scale:
(eb) (bb)
c d e f g a b c d e f g a b c d
[44] [64]
(28) (42) [66]
24 27 30 32 36 40 45 48 54 60 63 72 81 90 99 108
The partial-numbers are also given for the resulting scale
at the bottom of the diagram, showing that 7th/F (= eb-28)
is weaker than 5th/C (= e-30), and 7th/C (= bb-42) is weaker
than 5th/G (= b-45).
Also note that 11th/F (= b-44), 16th/F (= f-64) and 11th/C
(= f-66) are all weaker still, thus I have included them in
square brackets. These overtones are not even mentioned by
Schoenberg.
An interesting by-product appears here:
The two tones e and b appear in the first octave, but e is challenged by eb,
b by bb. That explains why it was once questioned whether the third was a
consonance, and shows why b [bb] and h [b] appear in the German tone alphabet.
[Carter, p 25:]
* Perhaps that also explains why there were church modes: The effect of a fundamental tone was felt, but since no one knew which tone it was, all of them were tried. And the accidentals are perhaps accidents in the mode chosen, but not in the natural, the basic one.
[note from Monzo: Anyone familiar with historical tuning theory knows that this explanation is silly. Schoenberg is speculating wildly here, and revealing his lack of historical knowledge; but at the same time, his imaginative theorizing is impressive. It is also interesting to me that the above-mentioned error by Carter in translating the German "b" into English "b" instead of "b-flat" occured right before the point where Schoenberg's text comments on exactly this notational difference.]
Whether the pioneers of music arrived at this scale through intuition or
through inference we cannot judge. It is unimportant anyway. We may
nevertheless take issue with theorists who set up complicated doctrines;
for, contrary to those doctrines, we have to give the discoverers credit
not only for instinct, but for the ability to reason as well. It is then
not at all impossigle that the right thing here was discovered by reason
alone, that therefore credit is due, no to the ear alone, but in part to
inference. We are not the first who can think!
[p 24]
[Carter, p 26:]
The discovery of our scale was a stroke of luck in the development of our
music, not only with regard to its success, but also in the sense that we
could just as well have found a different scale, as did for example the Arabs,
the Chinese and Japanese, or the gypsies. That their music has not evolved
to such heights as our does not necessarily follow from their imperfect scales,
but can also have to do with their imperfect instruments or with some other
circumstance which cannot be investigated here. Moreover, it is not to our
scale alone that we owe the evolution of our music. And above all; this
scale is not the last word, the ultimate goal of music, but rather a
provisional stopping place. The overtone series, which led the ear to it,
still contains many problems that will have to be faced. And if for the
time being we still manage to escape those problems, it is due to little
else than a compromise between the natural intervals and our inability to
use them -- that compromise which we call the tempered system, which amounts
to an indefinitely extended truce. This reduction of the natural relations
to manageable ones cannot permanently impede the evolution of music' and
the ear will have to attack the problems, because it is so disposed.
Then our scale will be transformed into a higher order, as the church modes
were transformed into major and minor modes. Whether there will then be
quarter tones, eighth, third, or (as Busoni thinks) sixth tones, or whether
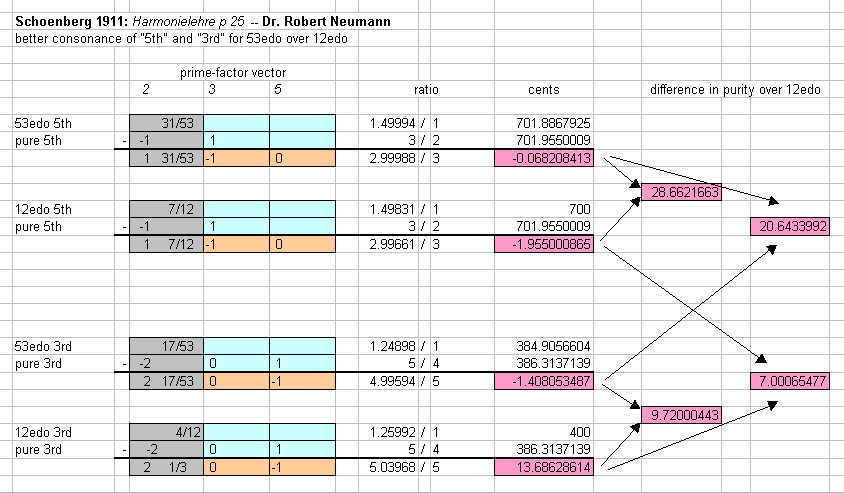
we will move directly to a 53-tone scale that Dr. Robert Neumann has
calculated *), we cannot foretell. Perhaps this new division of the octave
will even be untempered and will not have much left over in common with our
scale. However that may be, attempts to compose in quarter or third tones,
as are being undertaken here and there, seem senseless, as long as there are
too few instruments available that can play them. Probably, whenever the
ear and imagination
have matured enough for such music, the scale and the instruments will all at once be available. It is certain that this movement is now afoot, certain that it will lead to something.
*) Concerning his calculations, Dr. Robert Neumann has informed me
as follows (in part):
[from Monzo: This is not correct. 29edo and 41edo, while not as good as
53edo, both offer better approximations to the 3:2 "5th" than 12edo, and
41edo also gives a better approximation to the 5:4 "major 3rd" while
the 29edo "3rd" is only very slightly worse than 12edo. See my
analysis of
29 and 41edo compared to 12edo.]
The first step, anyway, is
to divide every semitone into two equal parts, whereby the octave would be
divided into 24 parts. Dividing again by 2, one could then obtain 48 parts.
1/48th of an octave and
1/53rd are almost the same size;
the 53-part
temperament, however, is preferable to the 48-part because of the much
greater purity of the consonances. The 48-part system has of course the
same basic intervals as appear in our 12-part temperament, from which it
is derived.
Now our tempered fifth is indeed already pure, but that of
the 53-part system is about 282/3
times purer; the third of
the 53-part system is about 9 times purer than ours and is
even purer than our fifth, which is only 7 times purer than the third."
The average musician will laugh at such speculations and will not be inclined
to see their point. It is clear that, just as the overtones led to the 12-part
division of the simplest consonance, the octave, so they will eventually bring
about the further differentiation of this interval. To future generations
music like ours will seem incomplete, since it has not yet fully exploited
everything latent in sound, just as a sort of music that did not yet
differentiate within the octave would seem incomplete to us. Or, to cite
an analogy — which one has only to think through completely to see how
very relevant it is: The sound of our music will at that time seem to have
no depth, no perspective, just as Japanese painting, for example, affects
us as primitive compared with our own, because without perspective it lacks
depth.
"As more and more of the possible combinations of our twelve tempered
scale degrees are felt and used as harmony,
[p 25]
the stock of unused possibilities
is being gradually exhausted; and the continuing need for new harmonic
(and melodic) vocabulary will finally break through the boundaries of the
system. Then new systems of temperament with smaller intervals might come
about, later perhaps even complete independence and freedom in the use of
all conceivable intervals, all conceivable frequencies and combinations.
Now the division of the octave into 53 equal parts would be an example
of a new temperament that could come under practical consideration:
specifically, whenever music has advanced so far that there is need for
a system with about four times as many tones as we now have; and when
there is need (or more correctly, when there is again need) for the purest
possible intonation of the basic intervals -- those determined by the first
overtones -- but at the same time, no wish to do without the convenience of
a temperament. As intermediate stages between the 12 and the 53-part
division of the octave only multiples of 12 could be considered, thus,
division into 24, 36, and 48 parts; for with any other number of parts
there would be no sufficiently pure fifth.
[from Monzo:]
Below is an analysis of Neumann's statements:
[p 26]
It may be that here again many digressions
and errors will have to be overcome; perhaps these, too, will lead to
exaggerations or to the delusion that now the ultimate, the immutable has
been found. Perhaps here, once again, laws and scales will be erected and
accorded an aesthetic timelessness. To the man of vision, even that will not
be the end. He recognizes that any material can be suitable for art -- if it
is well enough defined that one can shape it in accordance with its supposed
nature, yet no so well defined that the imagination has no unexplored
territory left in which to roam, in which to establish mystical connection
with th universe. And since will can still hope that the world will long
continue to be a riddle to our intelligence, we can say in spite of all
Beckmessers that the end of art is not yet at hand.
Updated:
1999.06.05
2002.01.23
2002.09.14
2003.10.22 -- added semitone graph of overtone theory
|
or try some definitions. |