Modern music has centered interest on two problems: that of tonality, and that of dissonance. It cannot be said that the conflict regarding these questions is new, nor that it is waged with new weapons. On the contrary: just as all the battlefields of world history are constantly the scene of renewed strife, so, too, is this one; this also is a bettlefield in the historic sense.
Of course, it is not necessary for me to cite as proof the well-known precendents from the musical past. It is enough to recall the "Dissonance" -Quartet of Mozart and Hans Sachs' lines:
Ihr schlosset nicht im gleichen Ton,
Das macht den Meistern Pein;
Doch nimmt Hans Sachs die Lehr' davon;
Im Lenz wohl Mu¨ss' es so sein.
[Your closing key is not the same,
This gives the masters pain;
But Hans Sachs draws a rule from this;
In Spring it must be so, 'tis plain.]
In Spring!
We can say that in the development of art, it must always be as it is in Spring! One does what is necessary, tho it cause somebody else pain; one does what the situation demands, unconcerned about the approval or disapproval of others.
And the cause of music demands, as the history of art-battles shows, that the secret of the sounding tone be always pursued anew. The development of music is more dependent than any other art upon the development of its technique. A truly new idea - at least as musical history reveals - is hardly imaginable without significant changes in musical technique. The material of music offers inexhaustible possibilities; but every new possibility in turn demands a new kind of treatment, because it presents new problems or at any rate demands a new solution of the old one. Every tonal progreassion, every progression of even two tones, raises a problem which requires a special solution. Yet the further such tones are brought into relation and contrast with each other and with rhythm, the greater is the number of possible solutions to the problem, and the more complex are the demands made on the carrying out of the musical idea.
In no art, properly speaking, can one say "the same thing", the same thing which has been said once before, least of all in music.
An idea in music consists principally in the relation of tones to one another. But every relation that has been used too often, no matter how extensively modified, must finally be regarded as exhausted; it ceases to have power to convey a thought worthy of expression. Therefore every composer is obliged to invent, to invent new things, to present new tone relations for discussion and to work out their consequences. It is for this reason that the technique of music must develop so quickly and so peristently. In a methodic progresssion from the more simple to the more complex, one would hardly be aware of the inevitable changes in technique. But imagination does not ask about method, nor does it invent according to a graduated scale. Differences in technique therefore appear far more abrupt than they are in reality. When we realize that today the difference in the technique of the early Beethoven from that of the later is apparent only to the connoisseur, we can no longer understand the cry from the gallery at the premiere of Beethoven's 8th Symphony: "Es fällt ihm schon wieder nichts ein".1
As I have said, the battle today, as always in music, is fought for the cause of dissonance and tonality, around concepts that are not even now clearly enough defined. For the phenomena which they are intended to reveal have been in continuous development since the beginning of music. This compels us always to conceive them in a new way. Therefore we shall try in the main to define them in relation to our time, according to present conditions, without claiming eternal validity.
Let us first examine the concept of tonality.
This coincides to a certain extent with that of the key, in so far as it refers not merely to the relation of the tones with one another, but much more to the particular way in which all tones relate to a fundamental tone, especially the fundamental tone of the scale, whereby tonality is always comprehended in the sense of a prticular scale. Thus, for example, we speak of a C-major tonality, etc.
If, however, we wish to investigate what the relation of tones to each other really is, the first question that arises is: what makes it possible that a second tone should follow a first, a beginning tone? How is this logically possible?
The question is more important than it seems at first; nevertheeless to my knowledge it has not previously been raised. Altho all imaginable and far-reaching problems have been considered, no one has yet asked: How, after all, can two tones be joined one with another?
My answer is that such a juxtaposition of tones, if a connection is to be brought about from which a piece of music may be the result, is only possible because a relation already exists between the tones themselves.
Logically, we can only join things that are related, directly or indirectly. In a piece of music I cannot establish a relation between a tone and, let us say, an eraser; simply because no musical relation exists.
To elucidate the relationship between tones one must first of all recall that every tone is a compound sound, consisting of a fundamental tone (the strongest sounding one) and a series of overtones.2 We may now make the statement, and to a great extent test and prove it, that all musical phenomena can be referred to the overtone series, so that all things appear to be the application of the more simple and more complex relationships of that series.
Considered singly these relations are as follows:
1. The major scale is to be explained as nothing else than the addition of the tones of the 3 main triads on the I, IV and V degrees. In C-major they are, on the I degree: c-e-g; IV degree: f-a-c; V degree: g-b-d. But these tones again nothing other than the 4th, 5th, and 6th overtones of the 3 main fundamentals of a scale (dominant, tonic, subdominant), which the following table demonstrates:
| 1 | 2 | 3 | | 4 | 5 | 6 | | 7 | 8 | 9 | 10 | 11 | 12 | 13
| C | C | |G| | | c | e | g | | bb | c | d | e | f# | g | ab
| F | F | |C| | | f | a | c | | eb | f | g | a | b | c | db
| G | G | |D| | | g | b | d | | f | g | a | b | c# | d | eb
| | | |
The origin of the main fundamental tones is explained by the fact that each one occurs as the 3rd overtone of the one lying a fifth below it. So that C is the 3rd overtone of F, just as G is the 3rd overtone of C. In this manner G:C = C:F. And it is evident that C attracts the tones related to it thru G, just as F and its related tones do with the complex of C.
The natural origin of these fundamentals of the main degrees of the 3 main triads constructed on them, and of the resultant major scale from these components, as well as the circumstance that we actually to some extent hear and to some extent feel this relationship in every sounding tone, makes it possible for us to combine the tones of the major scale with one another.
2. But if we note the more distant overtones (up to the 13th) of these same fundamental tones, F, C, G (see the table above) we find the chromatic scale. Thus there appear:
| bb | as the | 7th | overtone of | C | |
|
| f# | as the | 11th | overtone of | C | |
|
| eb | as the | 7th | overtone of | F | and 13th of | G
| db | as the | 13th | overtone of | F | and 11th of | G
| ab | as the | 13th | overtone of | C | |
| | |
Of course the lower overtones that lie nearer the fundamentals are more easily perceptible than the higher, more distant ones. It is certain that the more perceptible overtones sound more familiar to the ear than those it hears but faintly; these last therefore remain strange to it. For that reason the chromatic scale is a somewhat more complicated tonal form than the major. And since, moreover, the chromatic scale levels the differences in the intervals, a fundamental tone can hardly be regarded as implied at the outset. On the contrary the significance of the tones changes in accordance with the manner in which one or the other is artificially made the fundamental. In each case we have seven other major scale tones and five other non-diatonic tones. In the major scale the relation of the tones to one another is firm and constant thru their relation to the fundamental, but in the chromatic scale the relation of the tones is variable and dependent entirely on whether one of the tones is regarded as a fundamental.
But let us bear in mind that the chromatic scale flows from the same source as the major: from the elements which are the constituents of every tone. The difference is only that the one imitates the natural sound up to the 6th overtone, while the other reaches about twice as far, to the 13th overtone; in other words, the chromatic scale brings the more distant overtones within the possibility of relationship.
[... TO BE CONTINUED!]
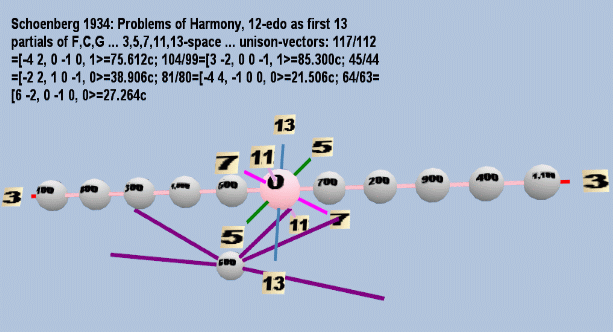
Below is a Tonescape® Lattice of the Tonespace for Schoenberg's description of 12-edo in 3,5,7,11,13-space, the periodicity-block bounded by the following unison-vectors:
![]()
![]()