Ramos's tuning as a periodicity block

© 1999 by Paul Erlich

Onelist Tuning Digest 382
Message: 19
From: Paul H. Erlich
Sent: Friday, November 05, 1999 6:13 PM
To: 'tuning@onelist.com'
Subject: RE: [tuning] tuning system of Ramos/Ramis

Manuel Op de Coul wrote,


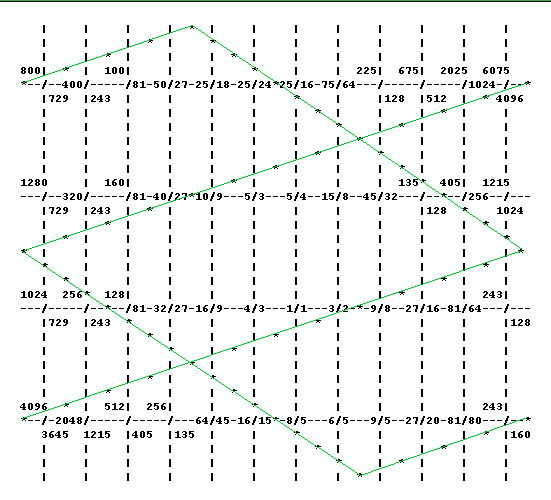
 135/128 10/9 32/27 5/4 4/3 45/32 3/2 128/81 5/3 16/9 15/8 2/1
 
Lattice:
 
     * * * * * *
 * * * * 0 *

Predictably enough, this can be construed as a Fokker periodicity block, this time with unison vectors of a syntonic comma (4 -1) and a
schisma (8 1):


 |4 -1|
 |    | = 4*1 - (8*(-1)) = 4 + 8 = 12
 |8  1|

Joe Monzo wrote,


 Ramos/Ramis [_Musica Practica_, Bologna, 1482]:
 
 
                    4/3---1/1---3/2---9/8---27/16---81/64
                    D      A     E     B      F#     C#
                    |      |     |     |
                    |      |     |     |
256/135---64/45---16/15---8/5---6/5---9/5
  Ab        Eb      Bb     F     C     G

Just transpose the above by 6:5 to get these ratios in the FPB [Fokker periodicity-block].

[Note from Monzo: In other words, the lattice given by Manuel and redrawn by Paul uses C = 1/1 as the reference. But Ramos actually used "A" as his reference, as in my diagram and the one like Paul's which would result from the transposition by 6:5.]

Back to where you were: Paul's A Gentle Introduction to Fokker Periodicity Blocks, part 2

Updated: 2000.1.20
By Joe Monzo

For many more diagrams and explanations of historical tunings, see my book.
If you don't understand my theory or the terms I've used, start here
or try some definitions.

I welcome feedback about this webpage:
corrections, improvements, good links.
Let me know if you don't understand something.

return to my home page

return to the Sonic Arts home page