Below is a post by Paul Erlich, which prompted some questions
from J Gill, and which I wanted to explain to J by making
some lattice diagrams showing what Paul explained.
First, here is the post by Paul, referring to my
comments on a previous tuning-list discussion about
my periodicity-block analysis of the Indian 22-sruti tuning.
> ______________________________________________
>
>
> Message #17:
>
> --- In tuning-math@y..., "monz" wrote:
> >
> > --- In tuning-math@y..., "Paul Erlich" wrote:
> >
> > http://groups.yahoo.com/group/tuning-math/message/14
> >
> > > --- In tuning-math@y..., graham@m... wrote:
> > >
> > > > Temper out the schisma from the periodicity block above.
> > > > You end up with a 24-note schismic scale. No way can that
> > > > have two step sizes!
> > > >
> > > > That looks like a refutation with the definitions I have.
> > >
> > > I think the problem is that, as you said before, the scale
> > > really has 12 pitch classes, not 24, due to the syntonic
> > > comma squared vanishing.
> > >
> > >
> >
> > Can you guys please illustrate all this with lattices and
> > other tables and diagrams?
>
> Hi Monz.
>
> What we're discussing here is the 24-tone periodicity block
> you came up with to derive the 22-shruti system of Indian music.
>
> The unison vectors of that periodicity block are the schisma
> and the diesis.
>
> As you can see, half the notes in that periodicity block
> differ from the other half by a syntonic comma. You can
> see that either in the lattice diagram or in the list of ratios.
>
> But here's the rub. If the schisma is a unison vector, and
> the diesis is a unison vector, then the schisma+diesis
> (multiply the ratios) is a unison vector. But you can verify
> that the ratio for the schisma times the ratio for the diesis
> is the square of the ratio of the syntonic comma. In other
> words, it represents _two_ syntonic commas.
>
> Now, if _two_ of anything is a unison vector, then the
> thing itself must be either a unison or a half-octave.
> But in your scale, the syntonic comma separates pairs
> of adjacent pitches, so it's clearly not acting as a
> half-octave. So it must be a unison. In a sense, it's
> logically contradictory to say that the schisma and diesis
> are both unison vectors while maintaining syntonic comma
> differences in the scale. The scale is "degenerate", or
> perhaps more accurately, it's a "double exposure" -- it
> seems to have twice as many pitch classes than it really has.
>
> As for Graham's matrix methods, I'd suggest that, rather
> than remain fairly confused indefinitely, you take a linear
> algebra course, or get a linear algebra book with exercises
> and solutions and work through it. Then, perhaps you might
> be able to make tremendous contributions of your own!
> Linear algebra is pretty abstract, so lattices, tables,
> and diagrams might never be able to get across some of
> the wisdom that Graham is making use of.
>
Next is a post by J Gill with discussion between he and
Paul about the unison-vectors, and about the scale J has
studied a lot, which is commonly known as the "Duodene"
devised by Alexander Ellis.
>
> --- In tuning-math@y...#580, "Paul Erlich" wrote:
> --- In tuning-math@y..., J Gill wrote:
> > Paul,
> >
> > In tuning-math message #17, in describing your analysis of
> > Monz's "24-tone periodicity block you" (Monz) "came up with
> > to derive the 22-shruti system of Indian music" you stated:
> >
> > > But here's the rub. If the schisma is a unison vector,
> > > and the diesis is a unison vector, then the schisma+diesis
> > > (multiply the ratios) is a unison vector. But you can verify
> > > that the ratio for the schisma times the ratio for the
> > > diesis is the square of the ratio of the syntonic comma.
> > > In other words, it represents _two_ syntonic commas.
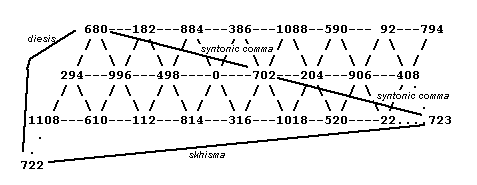
Here is a diagram illustrating what Paul is saying.
The diesis and skhisma are the two unison-vectors which
define "my" 24-tone periodicity-block. If they are
added together (i.e., multiply their ratios), they produce
a third unison-vector which is the sum of two syntonic commas.
(All lattices here follow the "triangular" convention, and
ratios are indicated on all of them by their cents-values.)
> > > Now, if _two_ of anything is a unison vector, then the
> > > thing itself must be either a unison or a half-octave.
> > > But in your scale, the syntonic comma separates pairs
> > > of adjacent pitches, so it's clearly not acting as a
> > > half-octave. So it must be a unison. In a sense, it's
> > > logically contradictory to say that the schisma and
> > > diesis are both unison vectors while maintaining syntonic
> > > comma differences in the scale. The scale is "degenerate",
> > > or perhaps more accurately, it's a "double exposure" --
> > > it seems to have twice as many pitch classes than it really
> > > has.
> >
> > I have been calculating the tonal generators and unison vectors
> > for the 12-tone scale made up of the interval ratios 1/1, 16/15,
> > 9/8, 6/5, 5/4, 4/3, 45/32, 3/2, 8/5, 5/3, 9/5, and 15/8 (which
> > is a subset of Monz's periodicity block related to the Indian
> > shruti system (1996), and which consists of the 12 interval
> > ratios which are centered (around the mid-point between the
> > 1/1 and 3/2 interval ratios) in a 3x4 rectangle of intervals
> > within Monz's matrix of interval ratios found on page 131 of
> > his "JustMusic: A New Harmony", 1996.
Here's Jay's scale:
> > The commatic unison
> > vectors I get are syntonic (81/80), diaschismic (2048/2025),
> > and a second syntonic (81/80), representing an (apparently)
> > "ill-conditioned" situation for linear algebraic analysis
> > (as a 5-limit system containing 3, as opposed to 2, commatic
> > unison vectors,
>
> Hmm . . . have you read the _Gentle Introduction to Periodicity Blocks_,
> including the "excursion" (the third webpage in the series)?
> It seems to me you may be confused about something.
>
>
> > (1) Could you explain further the meaning and implications of
> > your above statement, "Now, if _two_ of anything is a unison
> > vector, then the thing itself must be either a unison or a
> > half-octave.";
>
> Well, if two of something is a unison vector, then two of something is
> close to 0 cents, or close to 1200 cents, or close to 2400 cents, etc.
> (assuming the usual situation where the octave is the interval of
> equivalence). Then the something itself must be close to 0 cents, or
> close to 600 cents, or close to 1200 cents (which is equivalent to 0
> cents), etc. I.e. it must be either a unison of a half-octave.
>
>
> and
> >
> > (2) What can be done in tempering such a scale in order to
> > reduce the number of commatic unison vectors to 2, instead of 3
> > consisting of a "pair" of syntonic commas?
>
> Tempering does not decrease the number of unison vectors, though I
> still think you're confused about something that's leading you to
> count three unison vectors. 5-limit space with octave-equivalence is
> two-dimensional, so there can only be two different independent unison
> vectors for any periodicity blocks within that space (though
> additional, non-independent unison vectors, formed by "adding" or
> "subtracting" the two you start with, can be found, and in fact are
> relevant in many situations -- both the "excursion" and _The Forms Of
> Tonality_ give clear (I hope) examples of this.
>
> > I recognize that there may be no one simple answer to
> > this question, but would appreciate your thoughts in general
> > regarding what you might endeavor to choose to do in such
> > a case as this.
> >
> Perhaps you could supply some crude diagrams to help clarify what
> you're seeing? It would help me a lot in trying to answer your
> questions.
> __________________________________
>
> In "tuning-math" message #587
> >
> > > Hmm . . . have you read the _Gentle Introduction to
> > > Periodicity Blocks_, including the "excursion" (the third
> > > webpage in the series)?
> >
> > Yes, but my "absorption factor" remains "less than unity".
> > I will be re-reading it, with particular emphasis on your
> > periodicity block which includes those very interval ratios
> > (in the 12-tone JI system of which you ask is Ramos, and
> > Monz points out he believes it was from De Caus, with Manuel
> > Op de Coul pointing out it also Ellis' "Harmonic Duodene",
> > and your "excursion" in Part 3, as you suggested.
> >
> > > It seems to me you may be confused about something.
> >
> > > > Tempering does not decrease the number of unison vectors,
> >
> >
> > one *might* add, "but does alter the individual values of
> > those unison vectors, whose number is determined by the
> > prime limit of the system"???
>
> Exactly.
>
> >
> > I get the feeling that I may be simply be missing a fundamental rule
> > in the process of deriving unison vectors. I will run you through
> > what I have done, for your inspection and comment, below:
> >
> > "octave-reduced" interval ratios ordered in ascending numerical value
> > are: 1/1, 16/15, 9/8, 6/5, 5/4, 4/3, 45/32, 3/2, 8/5, 5/3, 9/5, 15/8.
Here's Jay's scale again:
ratio vector ~cents
2 3 5
(2/1 [ 1 0 0] 1200 interval of equivalence)
15/8 [-3 1 1] 1088
9/5 [ 0 2 -1] 1018
5/3 [ 0 -1 1] 884
8/5 [ 3 0 -1] 814
3/2 [-1 1 0] 702
45/32 [-5 2 1] 590
4/3 [ 2 -1 0] 498
5/4 [-2 0 1] 386
6/5 [ 1 1 -1] 316
9/8 [-3 2 0] 204
16/15 [ 4 -1 -1] 112
1/1 [ 0 0 0] 0
Because 2/1 is the interval of equivalence, this 2-dimensional
lattice diagram ignores it and shows only prime-factors 3 and 5:
> > "tonal generators" (with redundancies omitted, and in ascending
> > value) are: 25/24, 135/128, 16/15, 27/25.
>
> I'm not familiar with this concept of "tonal generators". Perhaps
> a term that would make more sense to me would be "step sizes"?
This diagram illustrates what Jay calls "tonal generators" and
what Paul calls "step sizes". They're simply the interval
distances which occur between each step of the scale when its
pitches are placed in "normal order" (i.e., A, Bb, B, ... G#, A).
> > "unison vectors" (as I imagine them...with reduncies RETAINED) are:
> > 81/80, 2048/2025, and 81/80.
>
> How are you obtaining that?
> >
> > Could it be that I am simply unaware that redundant results
> > for "unison vectors" (as in the case of the "tonal generators") are
> > to be OMITTED?
>
> I'm pretty sure, if I'm understanding you correctly, that
> the answer is "yes". However, for the 12-tone scale you
> mention, I'm surprised you didn't find 128/125 as one of the
> unison vectors.
>
> > Thus, I would report 2, rather than 3, resultant
> > vectors emerging from the above calculation...???
>
> There should be 2 . . . although 81/80, 125/128, and 2048/2025
> are three unison vectors for this scale, each of these is just
> a linear combination of the other two, as can be seen very easily
> from the vector notation of these three intervals:
>
> 81/80 = (4 -1)
> 128/125 = (0 -3)
> 2048/2025 = (-4 -2)
>
> So clearly,
>
> 81/80 = 128/125 "-" 2048/2025,
> 128/125 = 81/80 "+" 2048/2025,
> 2048/2025 = 128/125 "-" 81/80,
>
> where "+" is vector addition but multiplication of the ratios,
> and "-" is vector subtraction but division of the ratios.
Just to make it obvious what Paul is saying, I'll illustrate
the vector addition and subtraction which he's talking about:
81/80 = 128/125 "-" 2048/2025
[ 0 -3] = 128/125
- [-4 -2] = 2048/2025
---------
[ 4 -1] = 81/80
128/125 = 81/80 "+" 2048/2025
[ 4 -1] = 81/80
+ [-4 -2] = 2048/2025
---------
[ 0 -3] = 128/125
2048/2025 = 128/125 "-" 81/80
[ 0 -3] = 128/125
- [ 4 -1] = 81/80
---------
[-4 -2] = 2048/2025
These relationships can be shown plainly on the lattice:
OK, in all of the diagrams above where I designated Jay's scale,
I simply used arbitrary lines to draw the boundaries (altho the
ones on the right and left are pretty close to 128:125). Now we'll
use actual unison-vectors to see how it works. The unison-vectors
will be displaced slightly from the the actual ratio-points, so
that they can enclose the proper pitches; this doesn't affect
the way the mathematics works, because the length on the diagram
of any particular unison-vector is always the same, no matter
where it's placed.
As Paul noted, a 2-dimensional periodicity-block only requires
two independent unison-vectors to define it. Let's use
the two unison-vectors you started with, 81:80 = [4 -1] and
2048:2025 = [-4 -2].
The unison-vectors may be placed anywhere on the lattice, so
that many different periodicity-blocks, all with the same shape
and cardinality (in this case, 12), may result. I've chosen a
set of pitches which I know in hindsight can be manipulated so
as to eventually produce Jay's periodicity-block.
ratio vector ~cents
3 5
243/128 [ 5 0] 1110
9/5 [ 2 -1] 1018
27/16 [ 3 0] 906
8/5 [ 0 -1] 814
3/2 [ 1 0] 702
729/512 [ 6 0] 612
27/20 [ 3 -1] 520
81/64 [ 4 0] 408
6/5 [ 1 -1] 316
9/8 [ 2 0] 204
16/15 [-1 -1] 112
81/80 [ 4 -1] 22
By using the method of transposition that Paul explains in
the "excursion", we may split this block in half, for example:
and transpose half of it by one of the unison-vectors. Here
I'll illustrate what happens if we split off the right half of the
parallelogram and transpose it down by 81:80, :
so that we get:
ratio vector ~cents ratio vector ~cents
5/3 [-1 1] 884 from 27/16 [3 0] 906
5/4 [ 0 1] 386 from 81/64 [4 0] 408
15/8 [ 1 1] 1088 from 243/128 [5 0] 1110
45/32 [ 2 1] 590 from 729/512 [6 0] 612
4/3 [-1 0] 498 from 27/20 [3 -1] 520
1/1 [ 0 0] 0 from 81/80 [4 -1] 22
In each pair of notes, if we subtract the vector on the
left from the one on the right, the result is [4 -1] = 81:80,
showing that we've lowered each of the pitches on the right
by a syntonic comma.
The result is a new periodicity-block which retains all of
the properties of the old one, but has a new shape:
Can you see now why you found three unison-vectors of
81:80, 2048:2025, and 81:80 again? If you insist on
defining this particular block of pitches by those two
independent unison-vectors -- in other words, insisting
on keeping 2048:2025 as one of the edges -- then you get
a block whose actual boundaries are really defined by
81:80 and 128:125, but which is split in half
like this by the 2048:2025 unison-vector.
So if you say that 2048:2025 and 81:80 are the boundaries,
you have to look at it as a pair of complementary "periodicity
triangles" which are the mirror image of each other, and so you
must employ 81:80 separately on each half of the block, each
81:80 defining its own "periodicity-triangle". And 2048:2025
ends up being not really an edge, but an "internal homomorphism",
like the way the diagonal of a rectangle can define all four
of its edges at one stroke.
So it's really much better to define this particular
periodicity-block with the two independent unison-vectors
81:80 and 128:125 (the diesis), as Paul said:
In this diagram, the two unison-vectors are the heavy
boundary-lines which enclose the 12 pitches in Jay's scale.
Note that this pattern can be discerned on the diagram of
enharmonic D#s and Ebs on my Dictionary entry. It looks just
a bit different there, because there I used a rectangular
lattice and here I used a triangular one. If you imagine
the triangular lattice as a slanted version of the
rectangular one, the two unison-vectors should be obvious.
