* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
preliminary note:
SERIOUS TYPO ERROR IN
ENGLISH TRANSLATION OF HARMONIELEHRE
I've been writing for years about the
inconsistency
of Schönberg's notation of the 11th harmonic in the
diagram on p 24 in the Carter translation. Well, I was
just stunned to find out that in the 1911 German edition,
the 11th harmonic of F is written as "b", *which in
German means b-flat*!
(our "b" is written as "h").
The Carter translation gives it as "b", which equates
it with the 5th partial of G rather than the
correct equivalence intended by Schönberg, which
is with the 7th partial of C,
and so my writings on Schönberg's theories must be
revised. The diagrams here have all been corrected
to agree with the 1911 German edition.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
----- Original Message -----
From: monz
To:
Sent: Tuesday, January 15, 2002 11:10 PM
Subject: Re: [tuning-math] [tuning] Re: badly tuned remote overtones
> From: paulerlich
> To:
> Sent: Tuesday, January 15, 2002 5:09 PM
> Subject: [tuning-math] [tuning] Re: badly tuned remote overtones
>
>
> --- In tuning-math@y..., "monz" wrote:
> > > > I think one would *have* to include a 5-limit "enharmonic
> > > > unison-vector" here, since Schoenberg explicitly equated A#=Bb,
> > > > C#=Db, D#=Eb, etc., the usual 12-EDO enharmonically-equivalent
> > > > stuff.
> > >
> > > Did he do this explicitly within any of the 'constructions
> > > of unison vectors' you gleaned from him?
> >
> >
> > Well, not specifically *this* interval. But according to his
> > notational usage, *any* of the 5-limit enharmonicities should apply.
>
> Right, but . . . did he apply any of them explicitly within any of
> the 'constructions of unison vectors' you gleaned from him?
> Otherwise, you're just "assuming the answer".
I wanted to attempt a more rigorous answer to this.
Back in July, when I started all this about Schoenberg, I wrote:
http://groups.yahoo.com/group/tuning-math/messages/516?expand=1
> Message 516
> From: monz
> Date: Wed Jul 18, 2001 5:16am
> Subject: lattices of Schoenberg's rational implications
>
>
> ...
>
> Schoenberg then extends the diagram to include the
> following overtones:
>
> fundamental partials
>
> F 2...12, 16
> C 2...11
> G 2...12
Here, I will further adapt Schoenberg's diagram to make
his explanation as clear as possible, by adding the
partial-numbers and the fundamentals, which are the two
factors which when multiplied together give the relative
frequency-number of each note. The fundamentals are
F = 4, C = 6, G = 9.
d = 12*9 = 108
c = 11*9 = 99
b = 10*9 = 90
a = 9*9 = 81
g = 8*9 = 72
f = 11*6 = 66
f = 16*4 = 64
(f = 7*9 = 63)
e = 10*6 = 60
d = 9*6 = 54 d = 6*9 = 54
c = 12*4 = 48 c = 8*6 = 48
b = 5*9 = 45
bb= 11*4 = 44
(bb= 7*6 = 42)
a = 10*4 = 40
g = 9*4 = 36 g = 6*6 = 36 g = 4*9 = 36
f = 8*4 = 32
e = 5*6 = 30
(eb= 7*4 = 28)
d = 3*9 = 27
c = 6*4 = 24 c = 4*6 = 24
a = 5*4 = 20
g = 3*6 = 18 g = 2*9 = 18
f = 4*4 = 16
c = 3*4 = 12 c = 2*6 = 12
f = 2*4 = 8
> (eb) (bb)
> c d e f g a b c d e f g a b c d
> [44] [64]
> (28) (42) [66]
> 24 27 30 32 36 40 45 48 54 60 63 72 81 90 99 108
>
>
> ...
>
> The partial-numbers are also given for the resulting scale
> at the bottom of the diagram, showing that 7th/F (= eb-28)
> is weaker than 5th/C (= e-30), and 7th/C (= bb-42) is weaker
> than 5th/G (= b-45).
>
> Also note that 11th/F (= b-44), 16th/F (= f-64) and 11th/C
> (= f-66) are all weaker still, thus I have included them in
> square brackets. These overtones are not even mentioned by
> Schoenberg.
Here are the pitches (in my 72-EDO HEWM notation) and
frequency-numbers on a lattice diagram:
C^
/ \99
/ \
/ \ A
F^ \ /81
/ \[66] \ /
/ \ \ /
/ \ \ D
Bb^ \ \ /27 54 108
\[44] \ B- \ /
\ \/90-._ \ /
\ /\45 ' G ---------------F<
\ / \ /18 36 72 /63
\ E- \ / /
\/60-._ \ / /
/\30 ' C ---------------Bb<
/ \ /12 24 48 /(42)
A- \ / /
40'-._ \ / /
20 ' F ---------------Eb<
8 16 32 [64] (28)
These are all the unison-vectors implied by Schoenberg's diagram:
E 5*6=30 : Eb 4*7=28 = 15:14
Bb11*4=44 : Bb 7*6=42 = 22:21
B 5*9=45 : Bb11*4=44 = 45:44
B 5*9=45 : Bb 7*6=42 = 15:14
F 16*4=64 : F 7*9=63 = 64:63
F 11*6=66 : F 16*4=64 = 33:32
F 11*6=66 : F 7*9=63 = 22:21
A 9*9=81 :(A 20*4=80) = 81:80
C 11*9=99 :(C 24*4=96) = 33:32
(The high "A" and "C" in parentheses are not explicitly indicated
by Schoenberg, but may be inferred from his theory.)
So the only 5-limit unison-vector indicated here is the 81:80
syntonic comma, and even that is only inferred but not stated.
Its applicability to his theory, as well as that of other
5-limit UVs, must be inferred from a careful study of other
explanations in _Harmonielehre_, as I indicated in my last post.
The 15:14 arises only in connection with the notes Schoenberg
himself placed in parentheses. The other UVs are explicitly
indicated by Schoenberg.
-------
I thought it worth pointing out that if the 15:14 is considered
as a unison-vector, a 7-tone periodicity-block results, i.e.,
the diatonic scale. But if instead 15:14 is considered a
*chromatic* vector, and thus is not included in the unison-vector
matrix, then a 12-tone periodicity-block results.
Worth pointing out, because in the climactic final three chapters
toward which all of _Harmonielehre_ builds, Schoenberg introduces
structures such as the whole-tone scale and its related augmented-type
chords; chords built completely in 4ths -- both perfect and altered --
and finally, completely free use of all the notes of the *chromatic*
scale ... all of this as Schoenberg describes it is based on 12-EDO
tuning. He makes
Thus, leaving out the chromatic-vectors so that we will get at least
12 distinct tones, the unison-vectors implied by Schoenberg's 1911
diagram are:
Bb11*4=44 : Bb 7*6=42 = 22:21
F 16*4=64 : F 7*9=63 = 64:63
F 11*6=66 : F 16*4=64 = 33:32
F 11*6=66 : F 7*9=63 = 22:21
A 9*9=81 :(A 20*4=80) = 81:80
C 11*9=99 :(C 24*4=96) = 33:32
Here is a better version of the lattice, with unison-vectors
indicated by dashed lines. (Note that this lattice is inverted
with respect to the one above.)
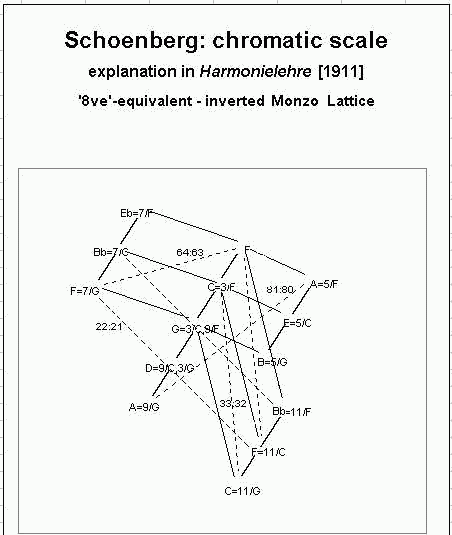As can be seen plainly on the lattice, these four unison-vectors
are not independent. Any one of the triplet 64:63, 33:32, and
22:21 (whose dashed lines form a triangle on the lattice)
can be found by multiplying the other two.
Then at the very end, a stunning coda speculating on _klangfarbenmelodie_:
(in which Schönberg feels compelled to offer his _credo_)
>> ... it must also be possible to make such progressions out of the
>> tone colors of the other dimension, out of that which we call simply
>> 'tone color', progressions whose relations with one another work
>> with a kind of logic entirely equivalent to that logic which satisfies
>> us in the melody of pitches. That has the appearance of a futuristic
>> fantasy and is probably just that. But it is one which, I firmly
>> believe, will be realized. I firmly believe it is capable of
>> heightening in an unprecendented manner the sensory, intellectual,
>> and spiritual pleasures offered by art. I firmly believe that
>> it will bring us closer to the illusory stuff of our dreams; that
>> it will expand our relationships to that which seems to us today
>> inanimate ...
>>
>> In such a domain, who dares ask for theory!
It's also worth pointing out that Schönberg's insistence on a
*12*-tone scale didn't appear in _Harmonielehre_ until the
revised version of 1922.
>> In Chapter IV, ... Schoenberg so extended his footnote
on the more minute subdivision of the octave that it is now
almost a chapter in itself. In the revised edition he went
on in this footnote to deny that further subdivision of the
octave was necessary as the next step beyond the tonal
(diatonic-chromatic) system. He went on to argue for the
use of twelve tones, elaborated polyphonically, as preferable,
at least for some time, to further proliferation of tones
within the octave. Finer subdivision of the octave Schoenberg
did not accept as, at that time, technologically feasible or
culturally necessary.
Whatever the reason for the lame ending in 1911, he did
continue in the revised edition. ... ...Perhaps
the latter statement merely makes clear what he had intended
to say in the first edition.
I'd say that there's much more in that statement, and its
revision, than Carter imagines. With the hindsight provided
by the knowledge of the microtonal experiments of Schönberg
and Webern in 1908, the 1911 comment clearly displays to me
Schönberg's still unabated interest in microtonality,
even as he rejected its systematic use for his own compositions
-- except for _sprechstimme_, which is an important exception,
and which bore its finest fruit the year after _Harmonielehre_
with _Pierrot Lunaire_.
Carter is right to carefully point out the differences
between the 1911 and 1922 versions of _Harmonielehre_.
But his focus seems to me to be on giving the clearest
presentation of Schönberg's *final* thoughts on the
subject, whereas my interest is wholly on determining
exactly what Schönberg was thinking in 1911.
[A LOT MORE TO COME HERE ABOUT SCHÖNBERG'S REVISIONS ]
. where M is the matrix composed of a set of i rational vectors
{u1/v1, u2/v2,... ui/vi} in which u1/v1 is a step-vector and
{u2/v2 ... ui/vi} are commatic or chromatic unison-vector
generators of the kernel, and
. where {h1, h2, ...hi} is the top row of M^-1, and
. where round() is the function which rounds to the
nearest integer,
for any non-zero a scale can be defined by calculating
for 0 <= n < d :
step[n] = (u1/v1)^round(h1(2)*n/d) * (u2/v2)^round(h2(2)*n/d)
* ... (ui/vi)^round(hi(2)*n/d) .
according to Gene's formula, here's the correct 12-tone
JI PB scale of rational implications for the unison-vectors
explicitly invoked by Schoenberg for the theory contained in
p 1-184 of the original edition of his _Harmonielehre_:
*****
Message 2798
From: "monz"
Date: Sat Jan 19, 2002 2:40 pm
Subject: deeper analysis of Schoenberg unison-vectors
> From: monz
> To:
> Sent: Saturday, January 19, 2002 8:01 AM
> Subject: Re: [tuning-math] ERROR IN CARTER'S SCHOENBERG (Re: badly tuned remote overtones)
>
>
> ... but if one is trying to ascertain
> the potential rational basis behind Schoenberg's work, how does
> one decide which unison-vectors are valid and which are not?
>
> Schoenberg was very clear about what he felt were the "overtone"
> implications of the diatonic scale (and later, the chromatic
> as well), but as I showed in my posts, the only "obvious"
> 5-limit unison-vector is the syntonic comma, and it seemed
> to me that there always needed to be *two* 5-limit unison-vectors
> in order to have a matrix of the proper size (so that it's square).
>
> (I realize that by transposition it need not be a 5-limit UV,
> but I'm not real clear on what else *could* be used, except for
> the 56:55 example Gene used.)
To make clear what I'm trying to say:
Let's begin with the unison-vectors clearly implied by
Schoenberg's 1911 diagram.
> From: monz
> To:
> Sent: Wednesday, January 16, 2002 3:43 AM
> Subject: [tuning-math] ERROR IN CARTER'S SCHOENBERG
>
> ... the total list of unison-vectors implied by Schoenberg's
> 1911 diagram [on p 23 of the original 1911 edition of
> _Harmonielehre_, p 24 in the Carter 1978 English edition] is:
>
> Bb 11*4=44 : Bb 7*6=42 = 22:21
> F 16*4=64 : F 7*9=63 = 64:63
> F 11*6=66 : F 16*4=64 = 33:32
> F 11*6=66 : F 7*9=63 = 22:21
> A 9*9=81 :(A 20*4=80) = 81:80
> C 11*9=99 :(C 24*4=96) = 33:32
>
> But because 22:21, 33:32, and 64:63 form a dependent triplet
> (any one of them can be found by multiplying the other two),
> this does not suffice to create a periodicity-block, which
> needs another independent unison-vector.
But now let's try to find the other unison-vector we need
from Schoenberg's musical examples.
If our 1/1 is called "C", in his overtone diagram, Schoenberg calls
"Eb" the "6th overtone [= 7th harmonic] of F", so that its
ratio is 7/6.
But then Schoenberg leaves the discussion of implied 7- and
higher-limit harmonies to the later chapters, and devotes
several chapters to explaining the diatonic major scale and
its harmonies, using C as a reference pitch and C-majoras the
reference scale and key. The diagram immediately before the
one referred to above is one in which he derives the diatonic
major scale from the first 6 harmonics of F, C, and G :
5:3-----5:4----15:8
A E B
/ \ / \ / \
/ \ / \ / \
4:3-----1:1-----3:2-----9:8
F C G D
This is standard stuff, going back to Zarlino (1558).
And as everyone here knows, a description of standard
diatonic chord progressions is going to bump into the
syntonic comma wherever a II-V progression is found,
which would imply a new D on our lattice at 10/9.
According to the expanded diagram of Schoenberg's explanation
of the overtone theory on p 23 [p 24 in Carter] (going up to
the 12th harmonics), the one I refer to at the beginning, the
81:80 syntonic comma is already a part of the system anyway.
He shows A as the 5th and 10th harmonics of F and as the
9th harmonic of G, which are the ratios 81:20 and 81:40,
which in turn are the syntonic comma plus 2 "8ves" and
1 "8ve" respectively. So we already have the unison-vector
of 81:80 = [-4 4 1] included in our kernel.
Schoenberg first introduces chromatic pitches in the chapter
"Die Molltonart" [p 110-128 in the original edition,
p 95-111 in the Carter edition]: F# and G# in the context
of A-minor.
To me, his explanation clearly implies a basis somewhere
between meantone and 5-limit JI: A-minor is seen as the
relative of C-major, so the note A is ~5/3. G# is always
regarded as a "leading-tone" and is assumed to be a consonant
~5/4 above the "dominant" E, which is assumed to be ~3/2
above the tonic A.
F# is always ~5/4 above D, the "subdominant", which is
assumed to be ~4/3 above the tonic A; thus, the 10/9
version of D is the one in effect here.
So our diatonic minor-scale paradigm lattice is:
25:18----( )---25:16
F# G#
/ \ / \ / \
/ \ / \ / \
10:9----5:3-----5:4----15:8
D A E B
\ / \ / \ /
\ / \ / \ /
4:3-----1:1-----3:2
F C G
and again the syntonic comma is in effect because, according
to Schoenberg's list of available minor-key chords on p 115
[p 99 in Carter], B can also be 50/27, F# can also be 45/32,
and D can still also be 9/8.
In a tiny handful of examples Schoenberg also introduces C#
as a sharpened "3rd" (= ~5/4) in the II chord in the key of
G-major.
So altogether up to this point we have this lattice:
50:27---25:18---25:24---25:16
B F# C# G#
\ / \ / \ / \
\ / \ / \ / \
10:9----5:3-----5:4----15:8---45:32
D A E B F#
\ / \ / \ / \ /
\ / \ / \ / \ /
4:3-----1:1-----3:2-----9:8
F C G D
These are the only pitches implied in any of Schoenberg's
explanations until the chapter "Modulation" [p 169-198 in
the original edition, p 150-174 in the Carter edition]. Thus,
excluding the prefatory chapters on aesthetics, about 1/3
of _Harmonielehre_ devoted to discussion of this simple
harmonic paradigm.
On p 184 [p 161 in Carter], music example number 110,
we see a D# in a musical example for the first time in
_Harmonielehre_. The first chord is a C-major triad, or
I in the key of C-major, which Schoenberg also designates
simultaneously as VI in E-minor. The second chord is a V
in E-minor, which is a B-major triad, and so its ~5/4 is
D# 75/64 :
50:27---25:18---25:24---25:16---75:64
B F# C# G# D#
\ / \ / \ / \ / \
\ / \ / \ / \ / \
10:9----5:3-----5:4----15:8---45:32
D A E B F#
\ / \ / \ / \ /
\ / \ / \ / \ /
4:3-----1:1-----3:2-----9:8
F C G D
So comparing this D# 75/64 with our Eb 7/6, now we finally
have a canditate for another 7-limit unison-vector, namely
225:224 = [-5 2 2 -1] .
So as of p 184 in _Harmonielehre_, we can construct as system
valid for Schoenberg's theories, as follows:
kernel
2 3 5 7 11 unison vectors ~cents
[ 1 0 0 0 0 ] = 2:1 0
[-5 2 2 -1 0 ] = 225:224 7.711522991
[-4 4 -1 0 0 ] = 81:80 21.5062896
[ 6 -2 0 -1 0 ] = 64:63 27.2640918
[-5 1 0 0 1 ] = 33:32 53.27294323
adjoint
[ 12 0 0 0 0 ]
[ 19 1 2 -1 0 ]
[ 28 4 -4 -4 0 ]
[ 34 -2 -4 -10 0 ]
[ 41 -1 -2 1 12 ]
determinant = | 12 |
mapping of ETs to UVs
[ 12 -7 12 0 12 ]
[ 0 1 0 1 -2 ]
[ 0 0 0 0 1 ]
[ 0 0 0 1 0 ]
[ 0 0 1 0 0 ]
This last matrix shows that 12-ET maps all of the
unison-vectors except 225:224 to 0 or 12 (i.e., unison),
correct?
And that the last three do not temper out the 81:80, 64:63,
and 33:32 respectively, correct?
Further illumation would be appreciated.
-monz
Message 2816
From: "monz"
Date: Sun Jan 20, 2002 3:05 pm
Subject: Re: [tuning-math] deeper analysis of Schoenberg unison-vectors
Hi Graham and Gene,
> From: monz
> To:
> Sent: Sunday, January 20, 2002 2:39 AM
> Subject: Re: [tuning-math] deeper analysis of Schoenberg unison-vectors
>
>
> >
> > > Message 2798
> > > From: "monz"
> > > Date: Sat Jan 19, 2002 2:40 pm
> > > Subject: deeper analysis of Schoenberg unison-vectors
> > http://groups.yahoo.com/group/tuning-math/message/2798
> > >
> > > ...
> > >
> > > So as of p 184 in _Harmonielehre_, we can construct as system
> > > valid for Schoenberg's theories, as follows:
> > >
> > > kernel
> > >
> > > 2 3 5 7 11 unison vectors ~cents
> > >
> > > [ 1 0 0 0 0 ] = 2:1 0
> > > [-5 2 2 -1 0 ] = 225:224 7.711522991
> > > [-4 4 -1 0 0 ] = 81:80 21.5062896
> > > [ 6 -2 0 -1 0 ] = 64:63 27.2640918
> > > [-5 1 0 0 1 ] = 33:32 53.27294323
> > >
> > > adjoint
> > >
> > > [ 12 0 0 0 0 ]
> > > [ 19 1 2 -1 0 ]
> > > [ 28 4 -4 -4 0 ]
> > > [ 34 -2 -4 -10 0 ]
> > > [ 41 -1 -2 1 12 ]
> > >
> > > determinant = | 12 |
>
>
> > From: monz
> > To:
> > Sent: Sunday, January 20, 2002 12:08 AM
> > Subject: Re: [tuning-math] deeper analysis of Schoenberg unison-vectors
>
> UV map
>
> > [ 1 0 0 0 0 ]
> > [ 0 1 0 0 0 ]
> > [ 0 0 1 0 0 ]
> > [ 0 0 0 1 0 ]
> > [ 0 0 0 0 1 ]
>
>
> So in other words, the way Gene would write it:
>
> h12(225/224) = h12(81/80) = h12(64/63) = h12(33/32) = 0
> h12(2/1) = 1
>
>
> But how do you label those other four columns? Well, for
> the time being, I'll call them h0, g0, f0, and e0, respectively
> from left to right, so that:
>
> h0(2/1) = h0(81/80) = h0(63/64) = h0(33/32) = 0 , h0(225/224) = 1
>
> g0(2/1) = g0(225/224) = g0(63/64) = g0(33/32) = 0 , g0(81/80) = 1
>
> f0(2/1) = f0(225/224) = f0(81/80) = f0(33/32) = 0 , f0(64/63) = 1
>
> e0(2/1) = e0(225/224) = e0(81/80) = e0(64/63) = 0 , e0(33/32) = 1
>
>
> So, the 2nd and 4th column-vectors in the adjoint (h0 and f0,
> respectively) define two versions of meantone:
>
> - one (h0) in which 7 maps to the "minor 7th" = -2 generators,
> and which tempers out all the UVs except 225/224;
>
> - one (f0) in which 7 maps to the "augmented 6th" = +10 generators,
> and which tempers out all the UVs except 64/63;
>
> and both of which map 11 to the "perfect 4th" = -1 generator.
>
>
> But what about the 3rd and 5th column-vectors in the adjoint
> (g0 and e0, respectively)? What tunings are they? I don't get it.
>
> And what relevance to these other mappings have to Schoenberg's
> theory?
OK, the 5th column is like the one you already explained to
me before, where 11 is mapped to a note 1 generator more than
the 12-tET value, like on a second keyboard tuned a quarter-tone
higher. So I understand that.
The most I can do with the 3rd column is this: the GCD is 2,
so that's equivalent to dividing the 8ve in half, right?
Which makes the tritone the interval of equivalence? So if
I divide the whole column by 2, I get [0 1 -2 -2 -1]. So
does this tell me how many generators away from 12-tET this
tuning maps 3, 5, 7, and 11? And exactly what *is* the generator?
Thanks.
-monz
Message 2820
From: "genewardsmith"
Date: Sun Jan 20, 2002 4:49 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
> So in other words, the way Gene would write it:
>
> h12(225/224) = h12(81/80) = h12(64/63) = h12(33/32) = 0
> h12(2/1) = 1
Actually, I'd write it h12(2) = 12; by definition, in fact,
hn(2) = n.
> But what about the 3rd and 5th column-vectors in the adjoint
> (g0 and e0, respectively)? What tunings are they? I don't get it.
g0 is Twintone, aka Paultone. e0 sends everything to 0 mod 12, and is not a temperament.
> And what relevance to these other mappings have to Schoenberg's
> theory?
(1) It is consistent with twintone as well as meantone, and so is a 12-et theory
(2) It sends all your commas to 0 mod 12, so again it is a 12-et theory.
Message 2826
From: "genewardsmith"
Date: Sun Jan 20, 2002 6:23 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
> 1) Where is it written that 12-tET is consistent with both
> meantone and twintone? This kind of stuff needs to be
> in my Dictionary.
12-et is the only thing consistent with both twintone and meantone. The
twintone wedgie is tt = [-2,4,4,-2,-12,11] and the meantone wedgie is mt =
[-1,-4,-10,-12,13,-4]. We can take wedge products of the wedgie with either
vals (leading to intervals) or intervals (leading to vals); in particular we
have
mt ^ 64/63 = h12
tt ^ 81/80 = -h12
(according to the basis I used in my program). Hence h12 is the only thing
which works with both of them.
Taking wedge products of wedgies with vals gives us stuff like
mt ^ h22 = 225/224
tt ^ h15 = 63/64
and so forth.
> 2) How can we see that "it sends all your commas to 0 mod 12"?
> Is that what the adjoint's 5th column-vector ("e0") is saying?
Right--it sends everything to 0 but 33/32, and it sends that to 12.
Message 2834
From: "paulerlich"
Date: Sun Jan 20, 2002 8:41 pm
Subject: ERROR IN CARTER'S SCHOENBERG (Re: badly tuned remote overtones)
--- In tuning-math@y..., "monz" wrote:
>
> > From: paulerlich
> > To:
> > Sent: Friday, January 18, 2002 1:04 PM
> > Subject: [tuning-math] ERROR IN CARTER'S SCHOENBERG (Re: badly
tuned
> remote overtones)
> >
> >
> > --- In tuning-math@y..., "monz" wrote:
> > >
> > > I think you misunderstand me, Paul. I just mean that there's
> > > probably a good chance that at least some of the time,
Schoenberg
> > > thought of the "Circle of 5ths" in a meantone rather than a
> > > Pythagorean sense.
> >
> > I doubt it. For Schoenberg, the circle of 5ths closes after 12
> > fifths -- which is closer to being true in Pythagorean than in
most
> > meantones.
>
>
> I understand that, Paul ... but if one is trying to ascertain
> the potential rational basis behind Schoenberg's work, how does
> one decide which unison-vectors are valid and which are not?
Only ones he specifically pointed to are valid. If it's not enough to
give you a PB, it'll still give you a linear temperament, which
should be interesting enough!
> Schoenberg was very clear about what he felt were the "overtone"
> implications of the diatonic scale (and later, the chromatic
> as well), but as I showed in my posts, the only "obvious"
> 5-limit unison-vector is the syntonic comma, and it seemed
> to me that there always needed to be *two* 5-limit unison-vectors
> in order to have a matrix of the proper size (so that it's square).
In 5-limit, yes.
>
> (I realize that by transposition it need not be a 5-limit UV,
By transposition? Not sure what you're getting at, but none of the
unison vectors need to necessarily be 5-limit when constructing an 11-
limit PB.
> > > This reference to you is only meant to credit you for opening
> > > my eyes to the strong meantone basis behind a good portion of
> > > the "common-practice" European musical tradition.
> >
> > OK -- but you're confusing two completely unrelated facts -- that
> > 128:125 is just in 1/4-comma meantone, and that 128:125 is one of
the
> > simplest unison vectors for defining a 12-tone periodicity block.
>
>
> OK, I'm willing to take note of your point, but ... *why* are
> these two facts "completely unrelated"? Isn't it possible that
> there *is* some relation between them that no-one has noticed
> before?
128:125 is just in 1/4-comma meantone. If 128:125 is tempered out,
the meantone is transformed into 12-tET. Then again, you could just
as well temper 2048:2025 out of meantone and get 12-tET, or temper
32768:32805 out of meantone and get 12-tET. These intervals are not
just in 1/4-comma meantone. 128:125 is a UV of choice for this
purpose _only_ because it's the simplest, _not_ because it's just in
1/4-comma meantone.
Message 2837
From: "paulerlich"
Date: Sun Jan 20, 2002 8:58 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
> OK, the 5th column is like the one you already explained to
> me before, where 11 is mapped to a note 1 generator more than
> the 12-tET value, like on a second keyboard tuned a quarter-tone
> higher.
Hmm . . . quarter-tones should _not_ figure into an analysis of a 12-
tone periodicity block. Gene, am I missing something?
Message 2838
From: "genewardsmith"
Date: Sun Jan 20, 2002 9:01 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "paulerlich" wrote:
> Hmm . . . quarter-tones should _not_ figure into an analysis of a 12-
> tone periodicity block. Gene, am I missing something?
Quarter-tones have nothing to do with it--it's telling us that 11 is being
mapped inconsistently.
Message 2839
From: "paulerlich"
Date: Sun Jan 20, 2002 9:05 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
> > > > 2 3 5 7 11 unison vectors ~cents
> > > >
> > > > [ 1 0 0 0 0 ] = 2:1 0
> > > > [-5 2 2 -1 0 ] = 225:224 7.711522991
> > > > [-4 4 -1 0 0 ] = 81:80 21.5062896
> > > > [ 6 -2 0 -1 0 ] = 64:63 27.2640918
> > > > [-5 1 0 0 1 ] = 33:32 53.27294323
Here is the contents of the Fokker parallelepiped defined by these
UVs, at one (arbitrary) position in the lattice:
cents numerator denominator
84.467 21 20
203.91 9 8
315.64 6 5
386.31 5 4
498.04 4 3
590.22 45 32
701.96 3 2
813.69 8 5
905.87 27 16
996.09 16 9
1088.3 15 8
1200 2 1
It's pretty clear that most of the consonances will straddle across
different instances of the PB, rather than being contained mostly
within this set of JI pitches.
Message 2840
From: "paulerlich"
Date: Sun Jan 20, 2002 9:07 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
>
> Hi Graham,
>
>
> > From:
> > To:
> > Sent: Sunday, January 20, 2002 12:27 PM
> > Subject: [tuning-math] Re: deeper analysis of Schoenberg unison-
vectors
> >
> >
> > monz wrote:
> >
> > > The most I can do with the 3rd column is this: the GCD is 2,
> > > so that's equivalent to dividing the 8ve in half, right?
> > > Which makes the tritone the interval of equivalence? So if
> > > I divide the whole column by 2, I get [0 1 -2 -2 -1]. So
> > > does this tell me how many generators away from 12-tET this
> > > tuning maps 3, 5, 7, and 11? And exactly what *is* the
generator?
> >
> > The house terminology is that you have a period of tritone, but
the
> > interval of equivalence is still an octave.
>
>
> OK, sorry ... I realize that I should have made that distinction
> myself. But ... what *is* that distinction? Does "period of
tritone"
> mean that some form of tritone is the generator?
The 1/2-octave can be thought of as a generator in the same way that
1 octave can be thought of as a generator in the usual cases, say
meantone for example. Normally we refer to the _other_ generator as
_the_ generator, and 1/2-octave or 1 octave or 1/n octave as the
period. It's the interval of repetition.
Message 2842
From: "paulerlich"
Date: Sun Jan 20, 2002 9:12 pm
Subject: Re: lattices of Schoenberg's rational implications
--- In tuning-math@y..., "monz" wrote:
> > If you want a notation, yes. One which makes the matrix
> > unimodular, ie with determinant +-1.
>
>
> So what's the secret to finding that?
Forget it. I don't know why you want to bother with Gene's "notation"
here. The "notation" would allow you to specify just ratios
unambiguously. However, I think the only reality for Schoenberg's
system is a tuning where there is ambiguity, as defined by the kernel
<33/32, 64/63, 81/80, 225/224>. BTW, is this Minkowski-reduced?
Message 2843
From: "paulerlich"
Date: Sun Jan 20, 2002 9:16 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "genewardsmith" wrote:
> --- In tuning-math@y..., "monz" wrote:
>
> > 1) Where is it written that 12-tET is consistent with both
> > meantone and twintone? This kind of stuff needs to be
> > in my Dictionary.
>
> 12-et is the only thing consistent with both twintone and meantone.
I noticed that quite a long time ago. Practicing my 22-tET guitar is
a great lesson in twintone that I can apply back on my 12-tET guitar.
Same for 31-tET and meantone. Both guitars make me better at 12-tET.
Of course, 12-tET always sounds out-of-tune afterwards.
Message 2848
From: "genewardsmith"
Date: Sun Jan 20, 2002 10:20 pm
Subject: Re: lattices of Schoenberg's rational implications
--- In tuning-math@y..., "paulerlich" wrote:
However, I think the only reality for Schoenberg's
> system is a tuning where there is ambiguity, as defined by the kernel
> <33/32, 64/63, 81/80, 225/224>. BTW, is this Minkowski-reduced?
Nope. The honor belongs to <22/21, 33/32, 36/35, 50/49>.
Message 2850 of 2854 | Previous | Next [ Up Thread ] Message Index Msg #
From: "paulerlich"
Date: Sun Jan 20, 2002 10:48 pm
Subject: Re: lattices of Schoenberg's rational implications
--- In tuning-math@y..., "genewardsmith" wrote:
> --- In tuning-math@y..., "paulerlich" wrote:
>
> However, I think the only reality for Schoenberg's
> > system is a tuning where there is ambiguity, as defined by the
kernel
> > <33/32, 64/63, 81/80, 225/224>. BTW, is this Minkowski-reduced?
>
> Nope. The honor belongs to <22/21, 33/32, 36/35, 50/49>.
Awesome. So this suggests a more compact Fokker parallelepiped
as "Schoenberg PB" -- here are the results of placing it in different
positions in the lattice (you should treat the inversions of these as
implied):
0 1 1
84.467 21 20
203.91 9 8
315.64 6 5
386.31 5 4
470.78 21 16
617.49 10 7
701.96 3 2
786.42 63 40
933.13 12 7
968.83 7 4
1088.3 15 8
0 1 1
119.44 15 14
203.91 9 8
315.64 6 5
386.31 5 4
470.78 21 16
617.49 10 7
701.96 3 2
786.42 63 40
933.13 12 7
968.83 7 4
1088.3 15 8
0 1 1
119.44 15 14
155.14 35 32
301.85 25 21
386.31 5 4
470.78 21 16
617.49 10 7
701.96 3 2
772.63 25 16
884.36 5 3
968.83 7 4
1088.3 15 8
0 1 1
84.467 21 20
155.14 35 32
266.87 7 6
386.31 5 4
470.78 21 16
582.51 7 5
701.96 3 2
737.65 49 32
884.36 5 3
968.83 7 4
1053.3 147 80
Message 2852
From: "paulerlich"
Date: Sun Jan 20, 2002 11:44 pm
Subject: Re: deeper analysis of Schoenberg unison-vectors
--- In tuning-math@y..., "monz" wrote:
> > > But what about the 3rd and 5th column-vectors in the
> > > adjoint (g0 and e0, respectively)? What tunings are they?
> > > I don't get it.
> >
> > g0 is Twintone, aka Paultone.
>
>
> I still don't know what that is
http://www-math.cudenver.edu/~jstarret/22ALL.pdf
Especially the section, "Tuning the Decatonic Scale", page 22.
Message
From: graham@m...
Date: Mon Jan 21, 2002 6:02 am
Subject: Re: deeper analysis of Schoenberg unison-vectors
In-Reply-To: <005201c1a1f5$e389c180$af48620c@d...>
monz wrote:
> Hmmm ... but the signs are opposite, which I think is why I'm confused.
> If the mapping of both 3 and 11 showed "1", then it would be more
> understandable: 3 and 11 both map to the generator, which is somewhere
> in the vicinity of a tritone ... that makes sense to me. But here
> we have 1 and -1, respectively. I called this column g0, so from
> the adjoint, we have g0(3)=2 and g0(11)=-4. Does the sign not
> matter because the tritone splits the interval of equivalence
> exactly in half?
You can either have 3:1 or 11:1, tritone reduced, as the generator. Or
you could have either (3:1 the same as 1:11) or (1:3 the same as 11:1).
The latter makes sense, because 4:3 and 11:8 are already within the
tritone.
> And can you also explain how 5 and 7 both map to the same
> number of generators in this case?
5:4 is 386 cents, and 7:4 is 969 cents. Tritone-reduced, 7:4 is 369
cents. 386 and 369 cents are close enough to be approximated equal.
Note you can also go to , choose the
"temperaments from unison vectors" option (without the 2:1) and plug in
your unison vectors. It happens to give generators larger than an octave
currently, but that's not important.
> And yet again I ask:
>
> > And what relevance to these other mappings have to Schoenberg's
> > theory?
That's for to you to work out.
(related but out of sequence now)
2801 From: genewardsmith
Date: Sat Jan 19, 2002 3:56pm
Subject: Re: A top 20 11-limit superparticularly generated linear temperament list
--- In tuning-math@y..., "monz" wrote:
> But ... it would be really nice if you could explain, as
> only tw examples, exactly what all this means. Since I've
> already played around with these particular unison-vectors,
> explaining what you did here would help me a lot to
> understand the rest of your work.
>
>
> >
> > 19. Monzoid
This was number 19 on the list, in terms of a badness measure.
> > [1, 4, -2, -1, 4, -6, -5, -16, -16, 4]
This is the "wedgie". When standardized, there is a unique wedgie corresponding to each (non-torsion, non-equal) temperment. This is a linear temperament wedgie; in the 11-limit the planar temperament wedgies also have ten dimensions; however this wedgie is computed from three unisons or two ets, whereas a planar would be computed from two unisons or three ets.
> > [55/54, 64/63, 81/80, 385/384]
These are all the 11-limit superparticulars equal to or less than 49/48 which are commas of the temperament--meaning they are tempered out. Since there are four of them, there is a linear dependency, but we can generate Monzoid from three independent ones.
> > ets 5, 7
These are "standard" ets, which round off to the nearest integer when mapping primes; 12 is not on the list, but h5+h7 would be if I listed anything "nonstandard".
> > [[0, -1, -4, 2, 1], [1, 2, 4, 2, 3]]
This is the period matrix, in a way easier to print than as a
4x2 matrix. The first list is the first column, giving maps to primes of the generator, the second column is the octaves.
> > [.4181947520, 1]
> > a = 5.0183/12 = 501.8337024 cents
These are the two generators, the second being merely an octave, and the first being a slightly sharp fourth.
> > badness 269.9708171
> > rms 39.86372247
> > g 3.150963571
"Badness" is the flat badness measure, "rms" is an average value for how much, in cents, the 11-limit consonances are off (40 cents!), and
g is the average number of generator steps to get to a consonance (a mere 3.)
> > Number 46 Monzo
> >
> >
> > [64/63, 81/80, 100/99, 176/175]
45/44 does not appear only because 45/44 > 49/48, which I used as a cut-off.
> > ets 7, 12
This time, the "standard" h12 12-et map makes its appearance.
> > [[0, -1, -4, 2, -6], [1, 2, 4, 2, 6]]
> >
> > [.4190088422, 1]
> >
> > a = 5.0281/12 = 502.8106107 cents
A small difference in the size of the optimal generator, because Monzo maps 11 differently than Monzoid.
> > badness 312.5112733
> > rms 28.87226550
> > g 4.174754057
The different 11-map makes the 11-limit more accurate, but it takes more steps on average because 11 maps to -6 and not 1.
Schoenberg: unison-vectors,
p 1-184, Harmonielehre (1911)
<225/224, 81/80, 63/64, 33/32>
Results from Graham Breed’s temperament calculator
http://microtonal.co.uk/cgi-bin/uvsurvey.cgi
unison vectors
225:224
81:80
64:63
lower limit, got an ET (12, 19, 28, 34)
unison vectors
225:224
81:80
33:32
calculated
unison vectors
33:32
55:54
77:75
0/1, 1892.5 cent generator
basis:
(1.0, 1.57708393667)
mapping by period and generator:
[(1, 0), (0, 1), (-4, 4), (-13, 10), (5, -1)]
mapping by steps:
[(1, 0), (-1, 1), (-8, 4), (-23, 10), (6, -1)]
highest interval width: 11
complexity measure: 11 (12 for smallest MOS)
highest error: 0.036516 (43.819 cents)
unison vectors
225:224
64:63
33:32
calculated
unison vectors
33:32
64:63
242:225
0/1, 1908.8 cent generator
basis:
(0.5, 1.59064251985)
mapping by period and generator:
[(2, 0), (0, 1), (11, -2), (12, -2), (10, -1)]
mapping by steps:
[(2, 0), (-1, 1), (13, -2), (14, -2), (11, -1)]
highest interval width: 4
complexity measure: 8 (10 for smallest MOS)
highest error: 0.061434 (73.721 cents)
unison vectors
81:80
64:63
33:32
calculated
unison vectors
22:21
33:32
36:35
0/1, 1902.9 cent generator
basis:
(1.0, 1.58576219547)
mapping by period and generator:
[(1, 0), (0, 1), (-4, 4), (6, -2), (5, -1)]
mapping by steps:
[(1, 0), (-1, 1), (-8, 4), (8, -2), (6, -1)]
highest interval width: 6
complexity measure: 6 (7 for smallest MOS)
highest error: 0.066315 (79.577 cents)
3201 From: monz
Date: Sun Feb 3, 2002 2:43pm
Subject: a notation for Schoenberg's rational implications
I am here referring specifically to Schoenberg's 1911 theory
as introduced in his _Harmonielehre_, and not to his later
1927/34 theory articulated in the paper "Problems of Harmony"
(the latter was the basis for Partch's criticism).
I apologize for the long quotes, but want to be complete for
anyone who's interested in following this thread.
> Message 2819
> From: monz
> Date: Sun Jan 20, 2002 4:09pm
> Subject: Re: Re: lattices of Schoenberg's rational implications
http://groups.yahoo.com/group/tuning-math/messages/2819?expand=1
>
>
> Help!
>
> I set up an Excel spreadsheet to calculate the notes of
> a periodicity-block according to Gene's formula as expressed here:
>
>
> > Message 2185
> > From: "genewardsmith"
> > Date: Wed Dec 26, 2001 6:25 pm
> > Subject: Re: Gene's notation & Schoenberg lattices
> >
> >
> > ...
> >
> > For any non-zero I can define a scale by calculating for 0<=n >
> > step[n] = (56/55)^round(7n/d) (33/32)^round(12n/d)
> > (64/63)^round(7n/d) (81/80)^round(-2n/d) (45/44)^round(5n/d)
>
>
>
> It worked just fine for both of these examples ,
> the 7-tone and 12-tone versions.
>
>
>
> But for the kernel I recently posted for Schoenberg ...
>
> > kernel
> >
> > 2 3 5 7 11 unison vectors ~cents
> >
> > [ 1 0 0 0 0 ] = 2:1 0
> > [-5 2 2 -1 0 ] = 225:224 7.711522991
> > [-4 4 -1 0 0 ] = 81:80 21.5062896
> > [ 6 -2 0 -1 0 ] = 64:63 27.2640918
> > [-5 1 0 0 1 ] = 33:32 53.27294323
> >
> > adjoint
> >
> > [ 12 0 0 0 0 ]
> > [ 19 1 2 -1 0 ]
> > [ 28 4 -4 -4 0 ]
> > [ 34 -2 -4 -10 0 ]
> > [ 41 -1 -2 1 12 ]
> >
> > determinant = | 12 |
>
>
> ... it doesn't work. All I get are powers of 2.
>
> Why? How can it be fixed? Do I need yet another
> independent unison-vector instead of 2:1?
>
> ********
>
> Message 2822
> From: genewardsmith
> Date: Sun Jan 20, 2002 5:08pm
> Subject: Re: lattices of Schoenberg's rational implications
http://groups.yahoo.com/group/tuning-math/messages/2822?expand=1
>
>
> --- In tuning-math@y..., "monz" wrote:
>
> > > determinant = | 12 |
>
> > ... it doesn't work.
>
> This determinant is why. In my example, the determinant
> had an absolute value of 1, and so we get what I call a
> "notation", meaning every 11-limit interval can be expressed
> in terms of integral powers of the basis elements. You
> have a determinant of 12, and therefore torsion. In fact,
> you map to the cyclic group C12 of order 12, and the twelveth
> power (or additively, twelve times) anything is the identity.
>
> > Why? How can it be fixed? Do I need yet another
> > independent unison-vector instead of 2:1?
>
> If you want a notation, yes. One which makes the matrix
> unimodular, ie with determinant +-1.
>
>
> ******
>
>
> Message 2900
> From: monz
> Date: Tue Jan 22, 2002 3:34pm
> Subject: Re: Re: Minkowski reduction
> (was: ...Schoenberg's rational implications)
http://groups.yahoo.com/group/tuning-math/messages/2900?expand=1
>
>
> > From: paulerlich
> > To:
> > Sent: Tuesday, January 22, 2002 4:32 AM
> > Subject: [tuning-math] Re: Minkowski reduction
> > (was: ...Schoenberg's rational implications)
> >
>
> > > [monz]
> > > With variant alternate pitches written on the same line
> > > -- and thus with invariant ones on a line by themselves --
> > > these scales are combined into:
> > >
> > > 1/1
> > > 21/20 15/14
> > > 35/32 9/8
> > > 7/6 25/21 6/5
> > > 5/4
> > > 21/16
> > > 7/5 10/7
> > > 3/2
> > > 49/32 25/16 63/40
> > > 5/3 12/7
> > > 7/4
> > > 147/80 15/8
> > >
> > > ...
> > >
> > > One thing I did notice in connection with this, is that
> > > 147/80 is only a little less than 4 cents wider than 11/6,
> > > which is one of the pitches implied in Schoenberg's overtone
> > > diagram (p 23 of _Harmonielehre_) :
> > >
> > > vector ratio ~cents
> > >
> > > [ -4 1 -1 2 0 ] = 147/80 1053.2931
> > > - [ -1 -1 0 0 1 ] = 11/6 1049.362941
> > > --------------------
> > > [ -3 2 -1 2 -1 ] = 441/440 3.930158439
> > >
> > >
> > > So I know that 441/440 is tempered out.
> >
> > NO IT ISN'T! I believe it maps to 1 semitone given the set of unison
> > vectors you've put forward.
> >
> > > But I don't see
> > > how to get this as a combination of two of the other
> > > unison-vectors.
> >
> > YOU CAN'T!
>
>
> Oops... my bad. Thanks, Paul. I see it now. If "C" is Schoenberg's
> 1/1, the 147/80 is mapped to "B" but 11/6 is mapped to "Bb".
> This is precisely the note which was misprinted in the diagram in
> the English edition ... guess I accepted it for so long that I
> got confused.
The Schoenberg PBs i've been posting have been defined
entirely by commatic unison-vectors.
Paul also posted something about how i would need to include
a *chromatic* unison-vector in order to arrive at a Smithian
"notation" (... i've searched for that post but can't find it).
Well, i was thinking about this and realized that here the
441/440 is a perfect candidate for a chromatic unison-vector!
So i plugged it into my spreadsheet matrix in place of 2/1,
using the unison-vectors i derived directly from _Harmonielehre_
(rather than Gene's Minkowski-reduced ones):
kernel:
2 3 5 7 11 ratio ~cents
[-3 2 -1 2 -1] = 441:440 3.93016
[-5 2 2 -1 0] = 225:224 7.71152
[-4 4 -1 0 0] = 81:80 21.50629
[ 6 -2 0 -1 0] = 64:63 27.26409
[-5 1 0 0 1] = 33:32 53.27294
and got a unimodular adjoint (or is that unimodular inverse?):
adjoint:
[12 5 -2 19 12]
[19 8 -3 30 19]
[28 12 -5 44 28]
[34 14 -6 53 34]
[41 17 -7 65 42]
Here i see two alternative mappings to 12, in which the
only difference is h12(11)=41 or 42.
The pentatonic mapping is in there, and now there's also
one that goes to 19.
But what to make of that third column? the -h2(2)=-2
means that some form of tritone is the period, correct?
But how do i find the generator? Until i know what that is,
the other numbers don't make any sense ... do they?
And as Paul predicted, this time Gene's formula worked
like a charm, and i got the following JI PB scale:
degree ratio vector
2 3 5 7 11
( 12 2/1 [ 1 0 0 0 0] )
11 15/8 [-3 1 1 0 0]
10 16/9 [ 4 -2 0 0 0]
9 5/3 [ 0 -1 1 0 0]
8 8/5 [ 3 0 -1 0 0]
7 3/2 [-1 1 0 0 0]
6 10/7 [ 1 0 1 -1 0]
5 4/3 [ 2 -1 0 0 0]
4 5/4 [-2 0 1 0 0]
3 32/27 [ 5 -3 0 0 0]
2 9/8 [-3 2 0 0 0]
1 16/15 [ 4 -1 -1 0 0]
0 1/1 [ 0 0 0 0 0]
triangular lattice:
A E B
5:3.------.5:4-----15:8
/ \ ` F# ' / \ / \
/ \ 10:7 / \ / \
/ \ | / \ / \
Eb Bb F C G D
32:27----16:9-----4:3-------1:1------3:2-----9:8
\ / \ /
\ / \ /
\ / \ /
Db Ab
16:15----8:5
In my quest to find this notation, Paul has already
suggested that i "forget it", since Schoenberg clearly
meant for all of these unison-vectors to be tempered out
of his system.
But, more than once in _Harmonielehre_, Schoenberg did
indeed allude to a rational basis which might underlie the
compositions from his "free atonality" period, so i'm
very interested in examining that rational basis.
So, guys, am i on the right track with this one?
Paul, how does this scale compare with the PB you would
find by your method using these criteria?
-monz
3202 From: monz
Date: Sun Feb 3, 2002 7:10am
Subject: Re: a notation for Schoenberg's rational implications
Take 2 ...
Here's another JI PB for comparison, derived from 45:44,
which i had originally interpreted as a commatic
unison-vector -- thanks to the misprint i discovered in
the English translation (B instead of Bb for 11th/F),
and which led me down the wrong path for years -- but
which can now be used as a chromatic unison-vector.
kernel
2 3 5 7 11 ratio ~cents
[-2 2 1 0 -1] = 45:44 38.9057732
[-5 2 2 -1 0] = 225:224 7.7115230
[-4 4 -1 0 0] = 81:80 21.5062896
[ 6 -2 0 -1 0] = 64:63 27.2640918
[-5 1 0 0 1] = 33:32 53.2729432
adjoint
[12 -7 -2 7 12]
[19 -11 -3 11 19]
[28 -16 -5 16 28]
[34 -20 -6 19 34]
[41 -24 -7 24 42]
determinant = | 1 |
We still have the same two mappings to 12, as well as
the one to -2 (which i don't understand).
But this time, the mappings to 5 and 19 disappear and
are replaced by two "diatonic" mappings to 7, which
differ only in their mapping of prime-factor 7: the
first one sends it to the 20th degree, which is a "7th",
and the second sends it to the 19th degree, which is
a "6th".
Am i right about this?
And the JI periodicity-block scale derived from this
has only one note different from the one in my last post,
and that is the "tritone", which is 64:45 here instead
of 10:7 :
triangular lattice:
A E B
5:3------5:4-----15:8
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
Eb Bb F C G D
32:27----16:9-----4:3-----1:1------3:2-----9:8
/ \ / \ /
/ \ / \ /
/ \ / \ /
Gb Db Ab
64:45----16:15----8:5
-monz
Here are some Tonalsoft Musica lattices for Schoenberg's
11-limit conception of 12-edo:
Tonalosft Musica lattice: Schoenberg 12-edo
81/80 on 3, 225/224 on 5, 64/63 on 7, 45/44 on 11
Tonalosft Musica lattice: Schoenberg 12-edo
81/80 on 3, 225/224 on 5, 64/63 on 7, 33/32 on 11
