- the 4 "5ths" between C and E are tuned in 1/4-comma meantone: G = 5^(1/4), D = 5^(1/2), A = 5^(3/4), E = 5^1;
- all the rest of the "5ths" are tuned Pythagorean down from C and up from E: Db...C = 3^(-5...0) and E...F# = 3^(0...2) * 5 .
In "8ve"-equivalent terms, here's how Kirnberger III works:
if C = n^0,
So the next "5th" above F# would be C# 33 * 5 = ~92.17871646 cents, which is only a skhisma (~2 cents) higher than the Db 3-5 = ~90.22499567 cents which we have already derived. This ~2-cent difference is outside the tuning resolution of any human tuner of Bach's time, so that in effect the open well-tempered chain becomes a closed well-tempered cycle, and F# = ~Gb, Db = ~C#, Ab = ~G#, Eb = ~D#, Bb = ~A#, etc.
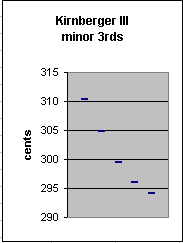
Well-temperaments have a rich variety of specific sizes for generic interval-classes. For example, Kirnberger III has :
Minor 3rds ---------- ~cents [3 5] vector instances 310 [ 0 -3/4] E:G, A:C 305 [-1 -1/2] D:F, B:D 300 [-2 -1/4] F#:A, G:Bb 296 [ 5 1 ] Db:E, Eb:F#, Ab:B 294 [-3 0 ] C:Eb, F:Ab, Bb:Db |
|
Because of the irrelevance of the skhisma, the 296-cent interval,
[5 1], which is the JI ratio 1215:1024, can be interpreted as
several different instances of the Pythagorean minor 3rd 32:27
= [-3 0] = ~294 cents, as follows:
Db:E = ~C#:E,, Db:~Fb
Eb:F# = ~D#:F#, Eb:~Gb
Ab:B = ~G#:B, Ab:~Cb
Note that the intervals F#:A and G:Bb are basically identical to the 12edo minor 3rds.
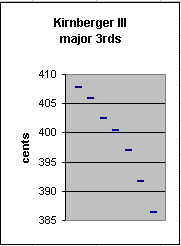
We can see that there's an even richer variety of major 3rds:
Major 3rds ---------- ~cents [3 5] vector instances 408 [ 4 0 ] Db:F, Ab:C 406 [-4 -1 ] E:Ab, F#:Bb, B:Eb 402 [ 3 1/4] Eb:G 400 [-5 -3/4] A:Db 397 [ 2 1/2] D:F#, Bb:D 392 [ 1 3/4] F:A, G:B 386 [ 0 1 ] C:E |
|
Because of the irrelevance of the skhisma, the 406-cent interval,
[-4 -1], which is the JI ratio 512:405, can be interpreted as
several different instances of the Pythagorean major 3rd 81:64
= [4 0] = ~408 cents, as follows:
E:Ab = E:~G#, ~Fb:Ab
F#:Bb = F#:~A#, ~Gb:Bb
B:Eb = B:~D#, ~Cb:Eb
Note that the interval A:Db is basically identical to the 12edo major 3rd. also note that in the case of the major 3rd, there are also intervals which are only +2 and -3 cents different from this one: Eb:G and (D:F#, Bb:D) respectively. i would say that all of this would automatically be equivalent as well, because they are also near the limit of tuning resolution.
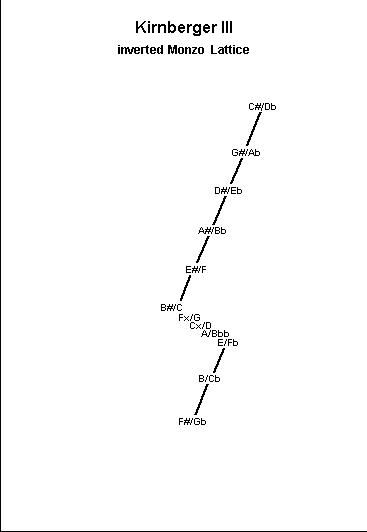
Below is a Monzo lattice-diagram of Kirnberger III tuning. [click on the diagram for an explanation of my lattice formula]
Note that, because of the equivalence described above in connection with the skhisma, the top and bottom ends of the lattice would wrap around to become a cylinder.
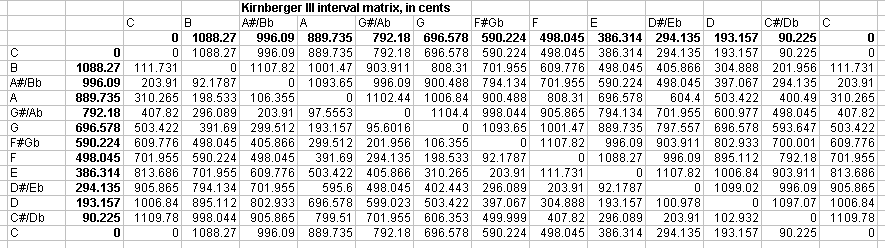
Below is the
interval
matrix for Kirnberger III, given in
cents:
Below is a table showing the cents values of the
3rds and 5ths for all major and minor triads in
Kirnberger III tuning:
major triads minor triads
3rds 5th 3rds
E 386.3137139 E 386.3137139
296.0887182 386.3137139
C# 90.22499567 696.5784285 C 0
400.4897103 310.2647146
A 889.7352854 A 889.7352854
Eb 294.1349974 D# 294.1349974
294.1349974 405.8662827
C 0 701.9550009 B 1088.268715
407.8200035 296.0887182
Ab 792.1799965 G# 792.1799965
D 193.1568569 D 193.1568569
304.8881422 397.0668587
B 1088.268715 696.5784285 Bb 996.0899983
391.6902863 299.5115698
G 696.5784285 G 696.5784285
C# 90.22499567 C# 90.22499567
294.1349974 400.4897103
A# 996.0899983 700.0012801 A 889.7352854
405.8662827 299.5115698
F# 590.2237156 F# 590.2237156
C 0 C 0
310.2647146 407.8200035
A 889.7352854 701.9550009 Ab 792.1799965
391.6902863 294.1349974
F 498.0449991 F 498.0449991
B 1088.268715 B 1088.268715
296.0887182 391.6902863
G# 792.1799965 701.9550009 G 696.5784285
405.8662827 310.2647146
E 386.3137139 E 386.3137139
Bb 996.0899983 G# 996.0899983
299.5115698 405.8662827
G 696.5784285 701.9550009 F# 590.2237156
402.4434311 296.0887182
Eb 294.1349974 D# 294.1349974
A 889.7352854 A 889.7352854
299.5115698 391.6902863
F# 590.2237156 696.5784285 F 498.0449991
397.0668587 304.8881422
D 193.1568569 D 193.1568569
Ab 792.1799965 G# 792.1799965
294.1349974 405.8662827
F 498.0449991 701.9550009 E 386.3137139
407.8200035 296.0887182
Db 90.22499567 C# 90.22499567
G 696.5784285 G 696.5784285
310.2647146 402.4434311
E 386.3137139 696.5784285 Eb 294.1349974
386.3137139 294.1349974
C 0 C 0
F# 590.2237156 F# 590.2237156
296.0887182 397.0668587
D# 294.1349974 701.9550009 D 193.1568569
405.8662827 304.8881422
B 1088.268715 B 1088.268715
F 498.0449991 F 498.0449991
304.8881422 407.8200035
D 193.1568569 701.9550009 Db 90.22499567
397.0668587 294.1349974
Bb 996.0899983 Bb 996.0899983
[from Joe Monzo, JustMusic: A New Harmony]
updated:
(to download a zip file of the entire Dictionary,
click here)
2002.11.20 -- added interval matrix
2003.05.21 -- added analysis of major and minor triads