The best way that I have discovered, to grasp as much harmonic information as possible in a just-intonation musical tuning system, is the use of lattice diagrams which portray pitches as points in multi-dimensional space connected by vectors.
In a just-intonation tuning system, each note is represented by a ratio which describes that note's relationship to another note, usually one that is used as a reference for the whole system. This reference tone has the ratio 1/1, also described as 1:1 or 1 to 1.
Any number can be factored into the series of prime numbers, each of which is a base which has an exponent that is either positive or negative, representing numbers >1 or <1, respectively, unless the exponent=0, which represents 1, the identity in multiplication.
Powers of 2 are all harmonically equivalent to this identity 1, thus, powers of 2 represent "octaves", and thus have no pronounced effect on the harmony, and may be eliminated, unless "octave" registration is specifically under consideration. Therefore the diagrams normally begin with prime-base 3.
My lattice diagrams treat each prime base as a unique
dimension in space, with all the exponents radiating
outward from the central 1/1, which is equivalent to
all numbers to the 0th power, or
n0.
Considered in 2-dimensional space, the vectors which
connect each exponent travel in
in a unique direction for each prime. This direction
is determined by the angle which represents the
cents value
(within the "octave") of that prime to the 1st
power, starting from 6 o'clock position.
Thus, 31,
which is the ratio 3/2 and is 702 cents, has a vector
radiating out from 1/1 at very close to 1 o'clock
position (because 6 + 7 mod 12 = 1).
51, which is the ratio 5/4 and is 386 cents,
has a vector radiating out at just less than 10 o'clock
position (6 + 3.86 = 9.86), and so on.
The negative exponents simply
radiate outwards from the opposite direction.
The vectors also vary in length and thickness
according to the prime-bases they are connecting,
with 3 the shortest and thickest.
Interestingly, even though 2-dimensional space was
the milieu in which these measurements were made, they
appear to they eye to form 3- or even more -dimensional
structures, somewhat resembling crystals.
Harry Partch
invented a structure he called the
"Tonality Diamond".
This shows all harmonic relationships
of ratios with numbers under a certain
"Odd Limit" (excluding
"octave doubling", or multiplication by 2, which he
used to keep each ratio within the same "octave", as
in most usual source scales).
These "diamonds", which simply get larger and hold
exponentially more ratios with each new further
odd-limit in Partch's version, take on a completely
different aspect when illustrated using my lattices.
The process certainly appeals to my artistic sensibilities.
I illustrate here the
5-Limit,
7-Limit, 9-Limit,
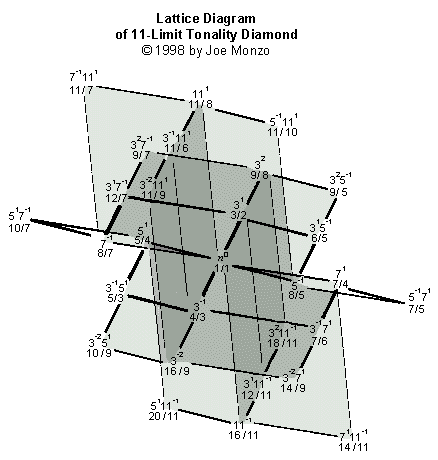
11-Limit, and
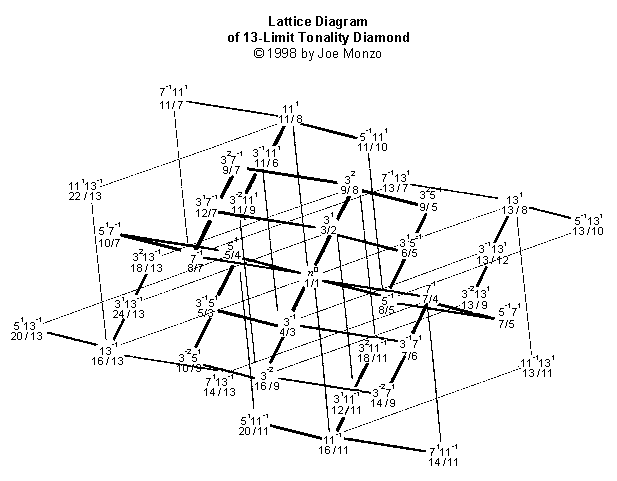
13-Limit
"Tonality Diamonds" as represented by
my lattice diagrams.
The symmetry which Partch noted in his scales and Tonality
Diamonds is readily apparent here, although the Tonality
Diamonds in this representation are not perfectly
symmetrical, as are some other systems I have devised.
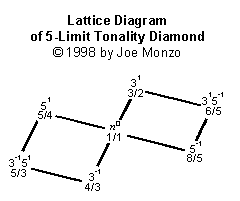
Partch called this the Incipient Tonality Diamond, because a triad with the proportions 4:5:6 gives the maximal consonance for a chord with three distinct identities, thus this is the simplest system that can be constructed which gives any real feeling of tonality.
The "major" triad on my lattice looks like this
(with odentities given):
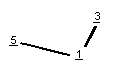
and the "minor" triad looks like this
(with udentities):
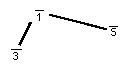
Note that the 5-Limit Lattice or Diamond contains 3 each of the "major" and "minor" triads. Each n-Limit system always contains (n+1) chords of maximal consonance, each with (n+1)/2 identities, evenly divided into (n+1)/2 each of "major" and "minor".
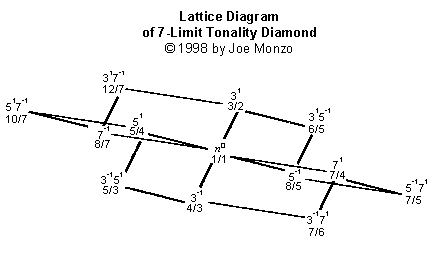
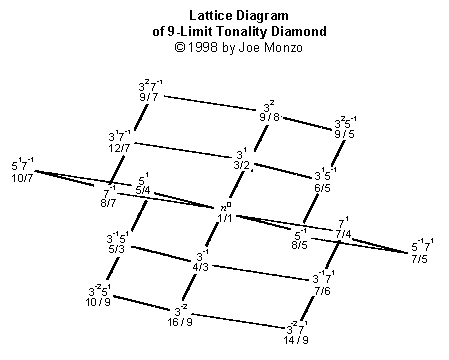
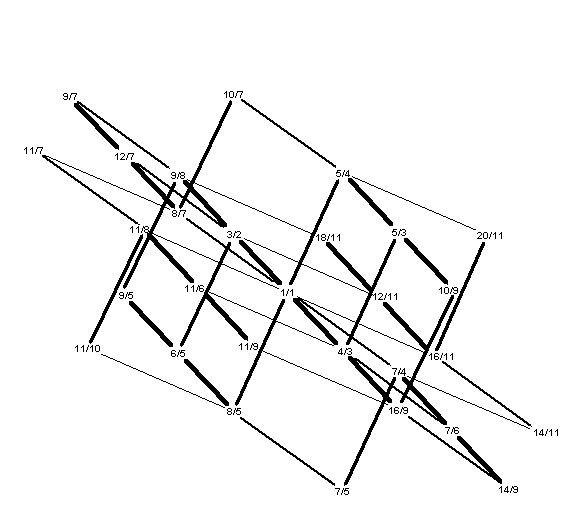
Note that the 9-Limit Lattice does not have a new
dimension -- it merely adds a layer, at either end of
the powers of 3, onto the 7-Limit Lattice. This is
because 9 is not a prime
number, but rather a composite, that is, a
number made up of other primes, in this case (This one may look better
on your system, but it takes a while to download.)
And most complicated of this set, the 13-Limit Lattice:
The lattices form intricate crystal-like structures that
show a wealth of harmonic information at a glance. If they
are viewed in the order listed above, it can be seen that
each smaller one is contained within the larger ones.
3 x 3, or 32.
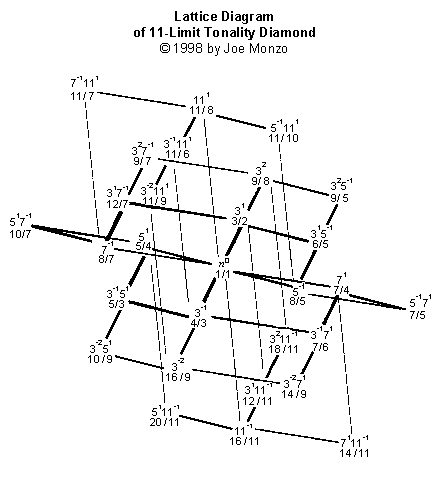
Here's a version
of the 11-Limit Lattice in full color:
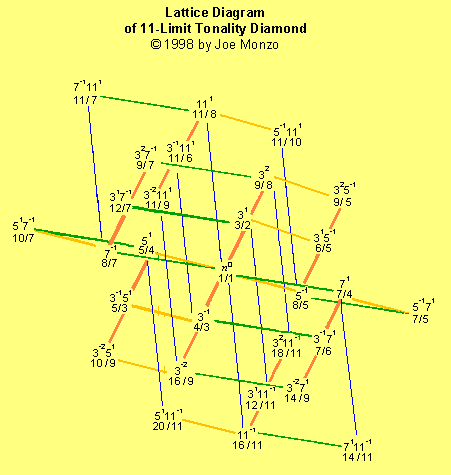
Next is a shaded version of the 11-Limit Lattice
which I like most of all: