A term coined by Joseph Saveur to designate the larger of his two interval measurements, the smaller being the heptameride.
A meride is calculated as the 43rd root of 2, or 2(1/43), with a ratio of approximately 1:1.016250325. It is an irrational number.
A meride is ~27.90697674 cents, or just a bit larger than several of the most common commas.
The formula for calculating the meride-value of any ratio is:
merides = log10(ratio) * [43 / log10(2)]
This interval therefore divides the "octave", which is assumed to have the ratio 2:1, into 43 equal parts. Thus a meride represents one degree in 43-EDO tuning.
One potential defect of using merides is that the familiar 12-EDO semitone does not come out with an integer number of merides, since 43 is a prime number and therefore does not divide evenly by 12. Thus, the 12-EDO semitone is ~3.583333333, or exactly 3 & 7/12, merides.
Note that 7 * 43 = 301, so both of Saveur's units, the merides and heptamerides, did divide evenly.
The interval which functions as the
"5th"
in 43-EDO is nearly identical to the
1/5-comma meantone "5th":
43-EDO "5th" = 2(25/43) = 25 merides = ~697.6744186 cents.
1/5-comma meantone "5th" = (3/2) / ( (81/80)^(1/5) )
=
2-(5/5) * 3(5/5) * 5(0/5) Pythagorean "perfect 5th", ratio 3:2
- 2-(4/5) * 3(4/5) * 5-(1/5) 1/5 syntonic comma
----------------------------
2-(1/5) * 3(1/5) * 5(1/5) = ~24.99925912 (= 24 ~1349/1350) merides = ~697.6537429 cents.
Difference between 43-EDO and 1/5-comma "5ths":
=
2-(125/215) 43-EDO "5th"
- 2-(43/215) * 3(1/5) * 5(1/5) 1/5-comma meantone "5th"
-------------------------------
2(168/215) * 3-(1/5) * 5-(1/5) = ~0.020675659 (= ~1/50) cent = ~1/2 jot.
Here is a graph of a 44-tone cycle of 1/5-comma meantone, centered on "C" as the reference (= generator 0):

Note that the pitches represented as Fbbb (-22 generators)
and C### (+21 generators) are nearly identical:
Fbbb = ( (3/2)-22 / ( (81/80)(-22/5) ) ) * 213
= 2(87/5) * 3-(22/5) * 5-(22/5)
= ~251.6176552 cents
C### = ( (3/2)21 / ( (81/80)(21/5) ) ) / 212
= 2-(81/5) * 3(21/5) * 5(21/5)
= ~250.7286019 cents
2(87/5) * 3-(22/5) * 5-(22/5) Fbbb
- 2-(81/5) * 3(21/5) * 5(21/5) C###
----------------------------
2(168/5) * 3(-43/5) * 5(-43/5) = ~0.88905332 (= ~8/9) cent.
0.88905332 / 43 = 0.020675659 --> compare with above.
Thus, limiting the meantone cycle to 43 pitches and distributing this difference equally among them, results in 43-EDO. The "chromatic semitone" = 3 merides, the "diatonic semitone" = 4 merides, and the "whole-tone" = 7 merides.
These are Gene Ward Smith's "7-limit MT reduced bases" for 43-edo:
43: [81/80, 126/125, 12288/12005]
which i would rewrite as a matrix of vectors thus:
2 3 5 7 [-4 4 -1 0] = 81/80 [ 1 2 -3 1] = 126/125 [12 1 -1 -4] = 12288/12005
1/5-comma meantone was first described by Abraham Verheyen in a letter to Simon Stevin, around 1600.
Below is a lattice which shows one pattern by which the plane of the [3 5] lattice is tiled by 43edo:
Below is a table of intervals, including all 23 intervals
which occur in a 12-tone subset of 1/5-comma meantone, and
some of the 43edo equivalents of those, as well as several
others in JI and in various other meantones.
--- prime-factor vector --- cents merides
2 3 5 7 11
8ve 1 1200 43
1/5cMT dim-1me 7/5 -7/5 -7/5 ~1116.423799 ~40
1/5-cMT maj-7th -1 1 1 ~1088.268715 ~39
1/5-cMT min-7th 2/5 -2/5 -2/5 ~1004.692514 ~36
12edo min-7th 5/6 1000 ~35 5/6
43edo aug-6th 35/43 ~976.744186 35
1/5-cMT aug-6th -2 2 2 ~976.5374295 ~35
7:4 -2 0 0 1 ~968.8259065 ~34 5/7
1/5-cMT dim-7th 9/5 -9/5 -9/5 ~921.1163135 ~33
1/5-cMT maj-6th -3/5 3/5 3/5 ~892.9612288 ~32
1/5-cMT min-6th 4/5 -4/5 -4/5 ~809.3850282 ~29
1/5-cMT aug-5th -8/5 8/5 8/5 ~781.2299436 ~28
25:16 aug-5th -4 0 2 ~772.6274277 ~27 2/3
1/5-cMT dim-6th 11/5 -11/5 -11/5 ~725.8088276 ~26
3:2 -1 1 ~701.9550009 ~25 1/7
12edo 5th 7/12 700 ~25
1/6-cMT 5th -1/3 1/3 1/6 ~698.3706193 ~25
43edo 5th 25/43 ~697.6744186 25
1/5-c MT 5th -1/5 1/5 1/5 ~697.6537429 ~25
1/4-c MT 5th 0 0 1/4 ~696.5784285 ~25
2/7-cMT 5th 1/7 -1/7 2/7 ~695.8103467 ~25
10:7 tritone 1 0 1 -1 ~617.4878074 ~22 1/8
1/5-cMT dim-5th 6/5 -6/5 -6/5 ~614.0775423 ~22
1/5cMT aug-4th -6/5 6/5 6/5 ~585.9224577 ~21
7:5 tritone 0 0 -1 1 ~582.5121926 ~20 7/8
11:8 -3 0 0 0 1 ~551.3179424 ~19 3/4
1/5-cMT p4th 1/5 -1/5 -1/5 ~502.3462571 ~18
4:3 2 -1 ~498.0449991 ~17 6/7
1/5-cMT aug-3rd -11/5 11/5 11/5 ~474.1911724 ~17
1/5-cMT dim-4th 8/5 -8/5 -8/5 ~418.7700564 ~15
12edo maj-3rd 1/3 400 ~14 1/3
43edo major-3rd 14/43 ~390.6976744 14
1/5-c MT major-3rd -4/5 4/5 4/5 ~390.6149718 ~14
5:4 -2 0 1 ~386.3137139 ~13 5/6
6:5 1 1 -1 ~315.641287 ~11 1/3
1/5-cMT min-3rd 3/5 -3/5 -3/5 ~307.0387712 ~11
12edo min-3rd 1/4 300 ~10 3/4
1/5-cMT aug-2nd -9/5 9/5 9/5 ~278.8836865 ~10
7:6 -1 -1 0 1 ~266.8709056 ~9 4/7
8:7 3 0 0 -1 ~231.1740935 ~8 2/7
1/5-cMT dim-3rd 2 -2 -2 ~223.4625705 ~8
9:8 -3 2 ~203.9100017 ~7 1/3
43edo tone 7/43 195.3488372 7
1/5-c MT tone -2/5 2/5 2/5 ~195.3074859 ~7
1/4-c MT tone 1/2 ~193.1568569 ~7
10:9 1 -2 1 ~182.4037121 ~6 1/2
1/5-cMT min-2nd 1 -1 -1 ~111.7312853 ~4
12edo semitone 1/12 ~100 ~3 3/5
1/5-cMT chr semitone -7/5 7/5 7/5 ~83.57620062 ~3
chromatic semitone -3 -1 2 ~70.67242686 ~2 1/2
43edo meride 1/43 ~27.90697674 1
Pythagorean comma -19 12 ~23.46001038 ~5/6
syntonic comma -4 4 -1 ~21.5062896 ~7/9
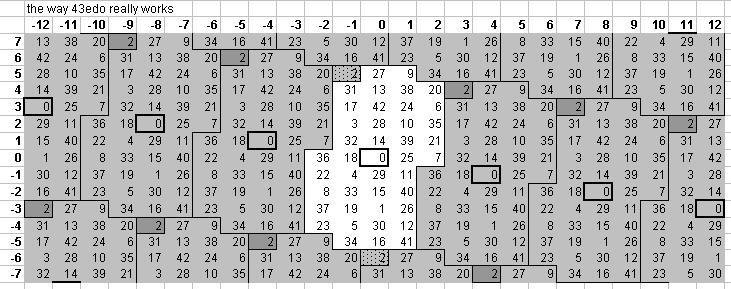
Below is a graphic showing a 7-limit "closest to 1/1" (by the taxicab metric) periodicity-block for 43edo, in which three 5-limit planes are shown side-by-side; exponents of 7 are 0, 1, and -1 from left to right.

Below is a plot of the points in a 3-dimensional Monzo lattice of the same 7-limit "closest to 1/1" periodicity-block for 43edo. In addition to the usual rectangular vertices, here i have also drawn lines connecting the doubled and trebled pitches (shown in darker grey in the "5-limit sheets" lattices above).

REFERENCES
Ellis, Alexander. 1885.
Appendix XX, in his translation of
Helmholtz, On the Sensations of Tone, p 437.
Dover reprint 1954.
[from Joe Monzo, JustMusic: A New Harmony]
Updated:
2002.11.13 -- 7-limit lattices added
2002.2.2
2001.11.8