Ever since I first heard it, this Scherzo has been one of my favorite Beethoven pieces. It was written originally for piano, which of course has a 12-tone fixed tuning; Beethoven's instrument may have been tuned in 12-eq, but its tuning was most probably a form of well-temperament, or could possibly have been one of the various meantone tunings.
Perhaps it is significant to the question of Beethoven's favored tuning for this piece that this was one of the piano sonatas of his that he arranged for String Quartet, in view of fact that the instruments of a string quartet are capable of an infinite variety of intonation.
I am presenting this MIDI sequence and its accompanying analysis as an evolving experiment in intonation. The indications are that what sounds 'right' - perhaps I should say 'sounds best to a particular listener' - is mathematically a lot more complicated than a system of simple integer ratios, which are too frequently assumed in a just-intonation analysis of classical music.
In Message # 8 in the Onelist Tuning Digest # 188, Paul Erlich commented:
Many classical pieces have been analyzed in just intonation and almost invariably they have a net downward drift in JI, sometimes by as much as half an octave.
This statement is entirely correct, and has been noted many times in the past, but after hearing this experiment, I must take issue with the methods of analysis to which Paul refers, and which have been used by almost all JI theorists.
As he argues, the results of psychoacoustical experiments must be taken into account when discussing tuning. But as I argue here (and Paul also agrees), the musical context of the work in question imposes quite stringent restrictions on which tuning choices sound 'right', and this includes mechanisms which prevent the tonal drift he mentioned.
It is highly questionable exactly what are the parameters we use in making these very subjective determinations, and they are certain to vary from person to person. But I think there are some guideposts which can be factored into the equation. In my case, a thoro knowledge of European tuning history and 'common-practice' [i.e., 1600 - 1900 AD] harmonic and contrapuntal theory, and decades of research into Beethoven's life, character, and musical compositions, were probably the most heavily weighted ingredients.
The indications are that the 'correct' set of pitches can be determined mathematically by use of Combination Product Sets, which can be modelled on tonal lattice diagrams, and which include 'rules' which make use of laterally-oriented pitch relationships rather than the more commonly assumed vertically-oriented 'harmonic' type of relationships. In actuality, a combination of both types of relationship come into play, but I think not enough emphasis has been given among JI theorists to the lateral orientation.
For Beethoven, I think it is reasonable to restrict a just-intonation interpretation mainly to a set of pitches contained within the 5-prime-limit, except perhaps in a few rare cases where the musical context (such as a long sustained chord) seems to demand a higher-prime (i.e., higher harmonic) interpretation.
I tuned it first using standard ideas about 5-limit JI, but found upon listening that this didn't work. The most obviously 'wrong' pitch was the 'leading tone' D#, which was too flat when tuned to D# - 3151 [= 15/8 = 10.88 Semitones], which is the consonant 'major 3rd [= 5/4] of the Dominant [V] chord.
I sharpened this to the Pythagorean leading-tone D# 35 [= 243/128 = 11.10 Semitones], which generally worked nicely, but this caused a further problem, because in several places - notably the end of the first phrase - the 'Dominant' [V] chord with a 'root' of B-major is the resolution at the end of a cadence, and must be correctly in tune [4:5:6 proportion].
So in cases where the V chord is used in passing and resolves onto the Tonic [I], the D# 35 is used with the 'simpler' B and F#, and in cases where the Dominant [V] is the end of the phrase, the B+ and F#+ have the large ratios which put them in tune with D# 35.
This is also conversely true of the 'root' E-minor chords, and in one place I've even used both 'B's at the same time.
Here's a blow-by-blow account of the first 8 measures, starting with the lattice diagram including the pitches I used. n0 = 'E', and the plus and minus signs indicate the tuning difference of a syntonic comma:
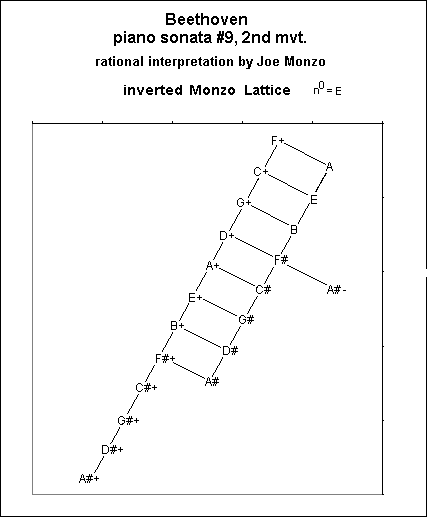
| bar 1: |
The opening E-minor chord is tuned to the usual 'minor' chord of 10:12:15:20 on the 'root' of E n0, with C+ 5-1 as the fundamental. In the melody, the 'lower-neighbor' D# is tuned to 35, the Pythagorean 'leading-tone'.
|
| bar 2: |
C-major, tuned to the usual 'major' chord of 4:5:6:8:10 on the 'root' and fundamental of C+ 5-1, with the same melodic line as above.
|
| bar 3: |
A triad subset of a diminished-7th chord with two 'octave'-doublings, tuned to 75:128:150:180:256 on the bass note of A# - 3251, with G+ 315-1 as the fundamental.
|
| bar 4: |
A triad subset of a minor-7th chord with two 'octave'-doublings, tuned to 5:9:10:12:18 on the 'root' and bass note of A 3-1, with the ensuing melodic figure using F# 32, E n0, and D# 35, to outline a 'diminished 7th' tetrad which functions as a 'dominant 7th flat 9th' with the 'root' (B) omitted.
The proportions for this 'dominant' chord are
|
| bar 5: |
Two 'tonic' E-minor chords, with a '1st-inversion dominant' in between on a 'root' and fundamental of B 31, but with the Pythagorean leading-tone D# 35 incorporated as a sharpened '3rd', giving the tetrad the proportions 48:81:128:192 (= 31:34:n0:31).
|
| bar 6: |
A very interesting shift: the first two beats are on the Dominant, but here I tuned the 'root' to B+ 355-1 and the '5th' to F#+ 365-1, so that the Pythagorean leading-tone is a consonant 5-identity in a 4:5:6 triad. Even more interesting is the fact that I used the flatter B 31 in the melody along with this triad, because the melodic line seemed to call for a note flatter than the one I used for the 'root', with the resulting dissonance creating a tension that decreases with the less dissonant sonority of the following A+ 335-1 in the melody. The proportions of these two chords are 405:648:1944:2560 (= 3451:34:35:51) and 405:648:1944:2304 (= 3451:34:35:32) on a fundamental of G+ 315-1. The last chord of E-minor has the same E and G+ as the 'tonic' chord (with 'octave'-doubling of E), but with the dissonant B+ 355-1 incorporated as the '5th', to keep that pitch the same as the root of the 'dominant' chord. The proportions of this chord are 160:243:640:768 (= 51:35:51:31) on a fundamental of C+ 5-1.
|
| bar 7: |
The chord on the first two beats is a consonant 1:2:5:6 on a 'root' and fundamental of B+ 355-1. Melodically, the third beat uses E n0 as the upper neighbor to the D# 35 in the alto voice, the Pythagorean leading-tone A#+ 3105-1 as the lower neighbor to the B+ 355-1 in the tenor voice, and in the melody, A 3-1 going to G+ 315-1. The melodic interval between this G+ and the next F#+ is an inversion of the Pythagorean 'leading-tone'. The proportions for these two chords are: on the first eighth-note, 93312:177147:491520:655360 (which is much easier to understand notated as its prime-factors 36:311:3151:51), and on the second eighth-note, 93312:177147:491520:589824 (easier to understand as 36:311:3151:32), on a fundamental of F+ 3-15-1. Despite the complexity of these proportions, the chord on the third beat here is pretty jazzy, and sounds 'right' to me in this tuning.
|
| bar 8: |
The first phrase ends with a half-cadence on the Dominant, which I tuned to a very consonant 1:2:5:6 on B+ 355-1, the point of all the tonal maneuvering in the previous two measures.
|
Obviously these shenanigans (especially bar 6), of such microtonal subtlety, are not possible on a regular piano, which after all is the instrument for which Beethoven conceived the piece. So in the minds of some folks, this kind of thing takes this tuning experiment out of the realm of being an 'interpretation' and really makes it a new 'arrangement'.
On the other hand, regarding the significance of his own orchestrations and the validity of an approach like mine, Beethoven is recorded as having responded to his own violinist Schuppanzigh's complaint of the difficulty of a part, "Do you really think I consider your whining little fiddle when the Creator speaks to me?!". This indicates to me that Beethoven fully recognized the limitations humans would impose on his conceptions, and had in his mind an unattainably perfect (in his lifetime) ideal instrument.
Strangely enough, altho this tuning sounds best to me for this first phrase, when it is immediately repeated an 'octave' higher in the next 8 bars, some of the chords didn't sound good tuned like this, and had to be altered. You can hear this in the MIDI sequence; I have yet to write out the analysis.