written February, 1990
Adapted and expanded for use as incidental music for the play Invisible Haircut, written, produced, and directed by Jeff Morris. Performed off-off Broadway (New York) December, 1993.
There is a brief passing-tone chord near the end of measure 2, which I left in 12-Eq on this sequence. It lasts such a short time that the intonation isn't really noticeable.
JustMusic
analysis (m = measure):
[In this analytical method,
utonalities have the
numerary nexus above the dividing-line
with the udentities below,
and vice-versa for the otonalities.]
In Partch's terminology, the letters-with-
numbers and exponents below or above the line
give the 1-identity of the
Otonality or
Utonality,
respectively. He would call
these "roots" as follows:
The stack of numbers alone, on the opposite side
of the line, are the
identities present
in the chord. I find my notation much
simpler than Partch's. If you understand
what I wrote above, then you could easily
reproduce the tune. It's also easy to visualize
the pitches on a
lattice with my notation.
I wrote it originally in 12-Eq, then figured
out common-tones on paper, which is how I got
those strange F and Bb chords in measure 4.
I've tried this kind of thing for other people's
(older) music and it didn't work, because the
high-prime common-tones throw the chord-roots
off into an odd-sounding high-prime key, but surprisingly
here, it sounds great!
Part of the reason why I left that passing-chord
in measure 2 in 12-Eq is because, by use of all the
common-tone relationships in the following chords,
I had to find a "break" in the tonal fabric somewhere,
and I decided to do it with the parallel descending
chords going from m 2 into m 3. So the chord in m 3
is the only significant chord in the 6-measure phrase that's not
closely related to the preceding chord. Making
the passing chord also unrelated (by leaving it in
12-Eq) helps to mask the "break".
There are some pretty "far out" chord changes in
there, and with the employment of the
5-limit
xenharmonic bridges
("unison vectors" as Fokker
called them) they could be well represented
in a simple 5-limit tuning!
Whether in 19- or in 5-limit,
it sounds MUCH better in
JI than in
12-Eq. The JI versions have a richness that
is entirely lacking in the 12-Eq version. When
you hear the JI first, the 12-Eq simply falls
flat, so to speak.
m 1 m 2 m 3 m 4 m 5 m 6
C n0
-----
F 3-1
------
[12-Eq E]
-----------
Eb 33 5-1 71
---------------
F 33 5-1
----------
1
5
3
15
3
9
5
3
1
5
15
9
5
3
1
5
15
9
5
3
1
5
15
9
11
19
7
5
3
1
19
13
5
7
1
1
3
1
5
15
9
9 5
13 1
5 3
7 5
1 1
--------------------
F 32 5-1 71 19-1
-----------
Bb 32 5-1
-----------------
Ab 5-1
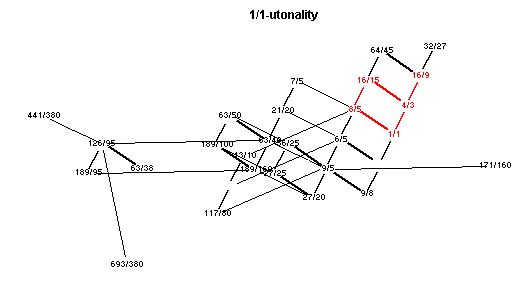
m 1 C 1/1 -Utonality
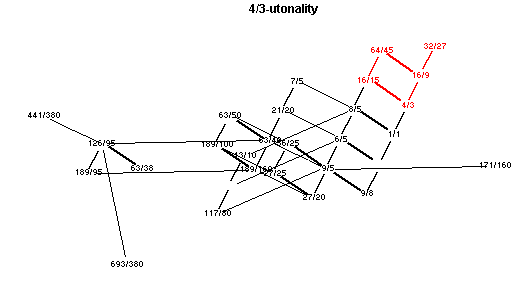
m 2 F 4/3 -Utonality
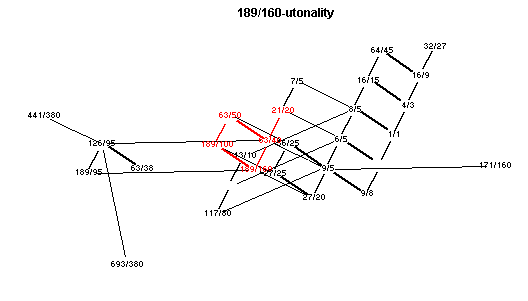
m 3 Eb 189/160-Utonality
m 4 F 126/95 -Otonality
Bb 9/5 -Otonality
m 5 F 27/20 -Utonality
m 6 Ab 8/5 -Otonality
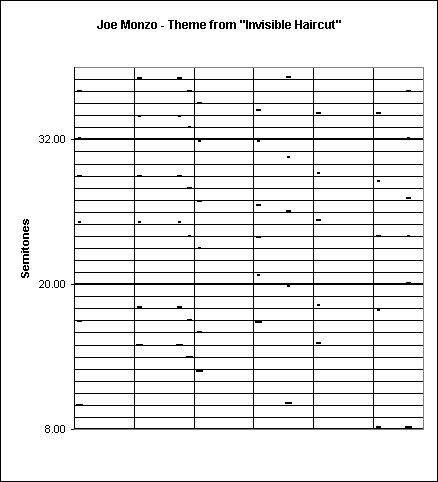
Joe Monzo: Invisible Haircut
lattice diagrams
lattice diagrams
Showing each of the main chords in red.
Click here to open a window with an animated applet of these lattices.
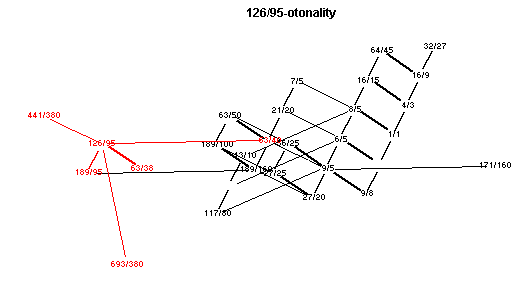
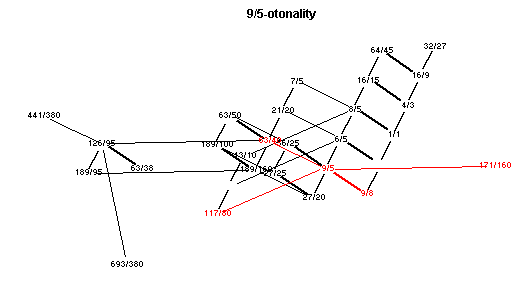
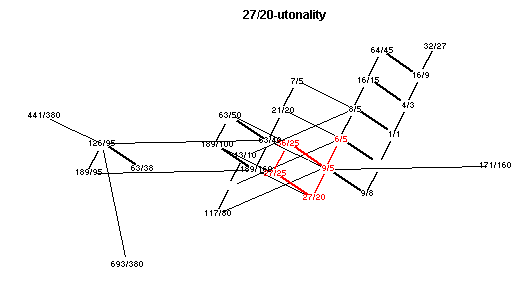
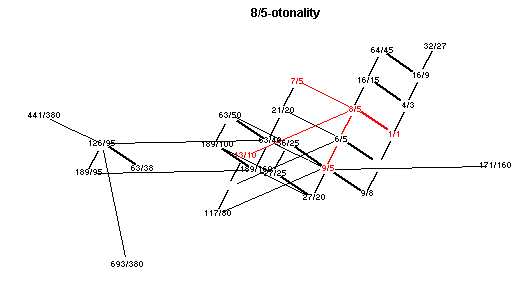
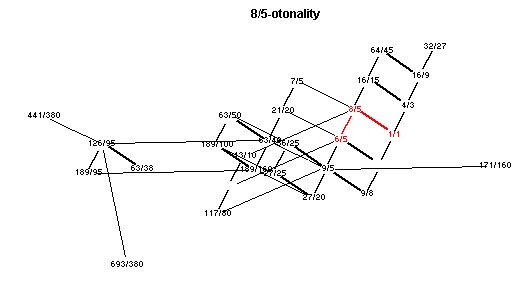
Click here to open a window with an animated applet of these lattices.
Some further observations on this piece:
Updated:
2002.09.14
2001.12.14
2000.10.04
2000.02.05
1999.03.09