©1999 by Joe Monzo
I recently added the plotting of pitches on my lattices along the prime-axis of 2. This gives me the ability to represent ETs, and also to represent 'octave'-specific ratios that are used in a tuning system, for example, those of the ancient Greeks, or Harry Partch's Monophonic system.
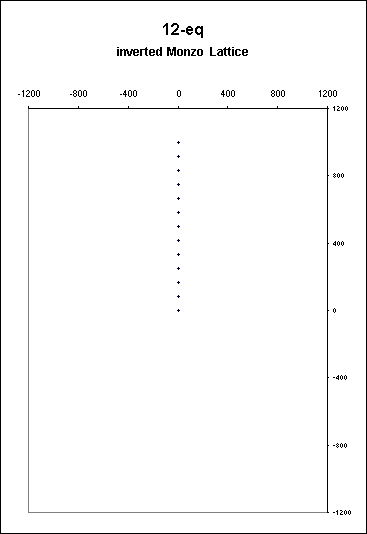
When I first plotted the 12-ET scale, I found something disturbing: as the pitch rose, the graph plots went *down* the page vertically. This would not do. I felt that it would be too disconcerting is the plot of a linear ET descended as the pitch it represent ascended, and that it must resemble more closely our perception of the rising and falling of the pitch. So the whole orientation of the lattice needed to be reversed.
This is OK with me, because the mathematical calculation of ratios as fractional powers of 2 and as integer powers of other primes is obviously the same operation, so I'll have to put up with the fact the my old lattices were 'upside down' - but the important thing is consistency of plotting between ETs and JIs.
A complaint has been lodged against my lattice plotting convention because it does not give an accurate representation of the 'pitch-height' or frequency of the tones in the system. This is no longer true, since now the 2-axis gives the familiar 'octaves' and represents the pitch-space in the usual way.
Actually, all the prime axes represent pitch-height in the same way, the difference as compared with 2 being that they never return to an 'octave' of the origin, whereas that is exactly what every power of 2 does.
But all these prime axes may be divided up into fractional parts in the same way that 2 has been divided into the equal temperaments. Indeed this has already been done with 3 by several microtonal composers, and with 5 in a famous example from Stockhausen, Gesänge der Junglinge. Meantones can also be viewed as a fractional division of the 1:5 ratio. For example, an interval calculated as the fourth root of 5, or 5(1/4), has a Semitone value of 6.97 [= ~696.578 cents], which is the size of a '5th' in '1/4-comma meantone'.
My interest is in studying the effects and affects of the different prime numbers in music, and 2 can now be seen on my lattices as simply another of the primes, in fact the first one.

Note that the scale is greatly magnified: the view above is only 2400 units square, whereas the Partch lattice shown below is 20,000 units square. The 2-axes have the shortest vector-length on the lattice, and so all the notes of an ET are crammed into this small space.
The inclusion of the ETs on my lattices multiplies vastly the number of bridges, as each ET itself has dozens of bridges to other ratios, in the same way that I've already described bridges among the higher primes, such as 225/224, an important 5--7 bridge.
As soon as I had incorporated these new plotting conventions, my attention turned toward graphing some intricate systems. I first tried Marchetto and then Ptolemy. There are not included here because the vectors have not yet been drawn.
(Remember the thread in the Tuning Forum regarding the 'music of the spheres'? Strangely enough, my plotted lattices (with no vectors) look like constellations of stars.)
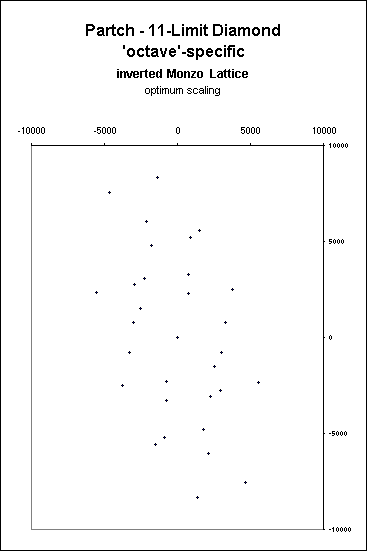
I definitely wanted to plot Partch's system because his
tonality diamond
is defined in his book1
as covering a
2-2/1 (2-'octave') span, and he specifies which 'octave'
each ratio lies in. 3/2 and 4/3 are doubled, and the first
time I plotted this lattice, I only put each of them in once
(i.e., the '29' notes of the diamond), and after I drew the
vectors, it looked lopsided and twisted.
So I made a new lattice with the correct doublings of those
two ratios (31 notes in all - hmmm....interesting number in tuning),
and it worked out beautifully.
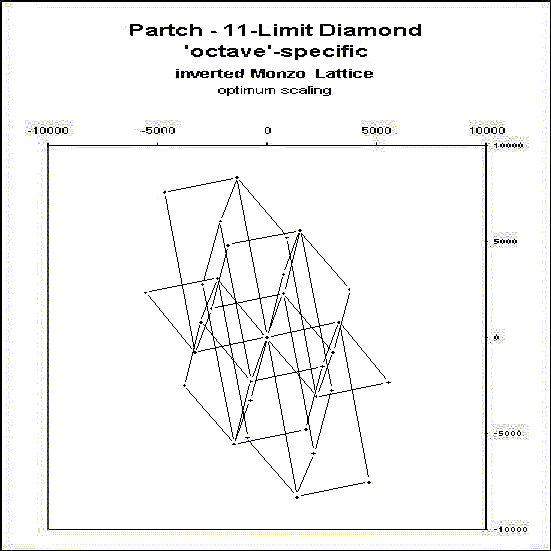
This is obviously still rudimentary, as it does not have any
ratios labelled, and it's not as attractive as my paper copy,
where I used solid vectors for the
otonal connections and
used dashed lines for the
utonal,
as did Partch on his diamond.
But I thought it interesting enough to share.
I am not yet entirely satisfied with this plotting convention.
But it's new, and perhaps it takes getting used to. I certainly
need to study many more tuning systems with it and compare them.
And it's also interesting to compare the 'octave'-specific and
'octave'-reduced versions of a lattice. My 'octave'-reduced
version of this 11-limit tonality diamond (in its old 'upside down'
form, but it still has the same shape) is in
my article on lattices.
Created 1999-4-20
Last Updated 1999-4-21
By Joe Monzo
1Harry Partch, 1974. Genesis of a Music,
I welcome
feedback about this webpage:
2nd edition, Da Capo Press, New York.
(bact to text)
or try some definitions.
corrections, improvements, good links.
Let me know if you don't understand something.
![]()
![]()