- my webpage 31edo as approximation of 1/4-comma meantone
- Margo Schulter's Yahoo Tuning List
message 29985
(Wed Nov 7, 2001 6:49 pm, Subject: Re: 31-EDO and 1/4-comma meantone compared). - For many more diagrams and explanations of historical tunings, see
my book.
- If you don't understand my theory or the terms I've used, start here
The most frequently encountered version of meantone tuning, and the only one in which the "whole-tone" is exactly the mean between the two commonly encountered "whole-tones" in just-intonation.
1/4-comma meantone is historically very important to the development of Western music, as the paradigms postulated by "common-practice" music-theory to a great extent depend on the elimination or tempering-out of the syntonic comma, which is probably the most prominent feature of all meantones.
Note that while in the familiar 12edo (which also belongs to the meantone family) there is a complete set of enharmonic equivalents, such that all 7 notes which have "flats" can also be "spelled" as 7 different notes which have "sharps", in all other meantones the "flats" are higher in pitch than supposedly enharmonically-equivalent "sharps", which is the opposite of the case in the much older Pythagorean tuning, and also the opposite of the case in the "expressive intonation" which has been widely taught in Eurocentric schools of playing since Beethoven's time (around 1800).
Based on my research, I would say that 1/4-comma meantone was the closest thing to a "standard" tuning in most of Europe from approximately 1500 to 1700, and was still commonly found on keyboards (especially organs) until about 1850. It would probably be fair to say that most instrumental music of the Renaissance and Baroque periods was intended to be played in 1/4-comma meantone or a close relative, and even after the growth in popularity of well-temperaments for keyboards after 1700, some form of meantone (generally more like 1/6-comma or 55edo) was usually still intended for orchestral music.
During Mozart's lifetime (late 1700s) orchestral players began using an "expressive intonation" which veered back towards Pythagorean, and Beethoven's musical language certainly encouraged the spread of 12edo, but to some extent meantone persisted in orchestral playing until approximately around the time of Wagner (mid-to-late 1800s). After the nearly universal adoption of 12edo, the loss of meantone was lamented by Mahler in the early 1900s. (see my webpage A Century of New Music in Vienna.)
1/4-comma meantone
tuning narrows each
'5th' in a series of '5ths'
by 1/4 of a
syntonic comma,
hence its name.
This results in 'perfect 5ths' of approximately 697
cents or 6.97
Semitones. Ascending "5ths"
will be flatter than just,
and descending "5ths" will be sharper.
The amount of tempering in 1/4-comma meantone is:
(81/80)(1/4) = (2-4 * 34 * 5-1)(1/4) = 2-1 * 31 * 5(-1/4)= ~5.376572399 cents = ~5 & 3/8 cents
So the 1/4-comma meantone "5th" -- the
generator --
is (3/2) / ((81/80)(1/4)). Using
vector addition,
that's:
2^ 3^ 5^
| -1 1 0 | = 3/2
- | -1 1 -1/4 | = (2-4345-1)(1/4) = (81/80)(1/4)
-----------------------
| 0 0 1/4 | = 1/4-comma meantone "5th"
= ~696.5784285 cents.
This has the effect of
tempering out the
syntonic comma so
that it vanishes, thus making 4 "5ths" minus 2 "8ves"
exactly equal to the
just
"major 3rd":
2^ 3^ 5^
| 0 0 4/4 | = 4 meantone "5ths"
- | 2 0 0 | = 2 "8ves"
-----------------------
| -2 0 1 | = just "major 3rd" = 5/4 = ~386.3137139 cents.
Assuming "octave"-equivalence
(i.e., the exponents of 2 are irrelevant to the construction of the
scale, so i've added 2-1 to the
vector here to put
the note into the reference "octave"),
the next note in the cycle after the "5th", that of
+2 generators,
is the "whole-tone"
2(-1)5(2/4) = ~193.1568569
cents. If we compare
this to the two JI
"whole-tones", subtracting the meantone from the larger
Pythagorean 9/8
and subtracting the smaller
5-limit 10/9
from the meantone, we find that it is indeed the exact
logarithmic mean between them:
2^ 3^ 5^
| -3 2 0 | = 9/8
- | -1 0 2/4 | = meantone
-----------------------
| -2 2 -2/4 | = ~10.7531448 cents.
2^ 3^ 5^
| -1 0 2/4 | = meantone
- | 1 -2 1 | = 10/9
-----------------------
| -2 2 -2/4 | = ~10.7531448 cents.
It was noted in 1691 by
Christiaan Huygens (and again
in the 1940s by Adriaan Fokker) that
31-EDO
was audibly indistinguishable from 1/4-comma meantone.
2(18/31) = 696.7741935 cents.
Using vector addition again to compare the 1/4-comma meantone "5th"
with the 31-EDO "5th", we get a difference between the two of:
2^ 3^ 5^
| 18/31 0 0 | = 31-EDO "5th"
- | 0 0 1/4 | = 1/4-comma meantone "5th"
-------------------------
| 18/31 0 -1/4 | = 31-EDO "5th" "-" 1/4-comma meantone "5th"
= ~0.195765082 cent = ~1/5 cent
= approximately the superparticular ratio 8844:8843
= as Huygens noted, about 1/110 syntonic comma
= almost exactly 1/10 grad or 6 tuning units.
(A Microsoft Excel spreadsheet showing all the calculations and the method used by Huygens is here.)
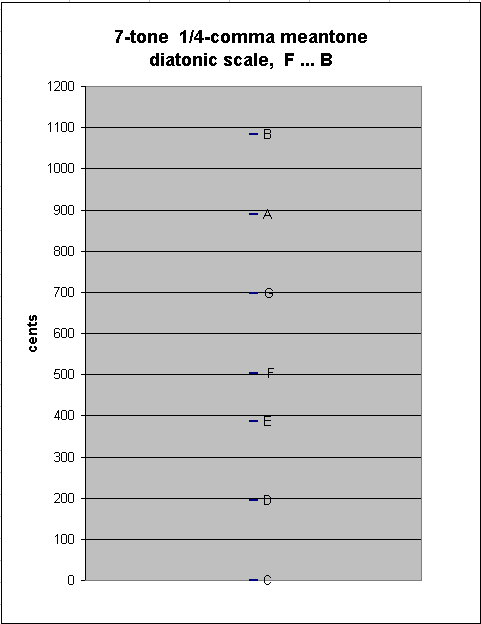
The 7-tone diatonic scale in 1/4-comma meantone contains only two "step" sizes: the ~193.1568569-cent "whole-tone" described above, between C:D, D:E, F:G, G:A, and A:B, and the ~117.1078577-cent "diatonic semitone" between E:F and B:C:
generator 8ves 5 ~cents
-1 1 * [-1/4] 503.4215715 "F"
4 - -2 * [ 4/4] 386.3137139 "E"
---------------------------
-5 3 * [-5/4] 117.1078577 1/4-comma meantone diatonic semitone ("minor-2nd")
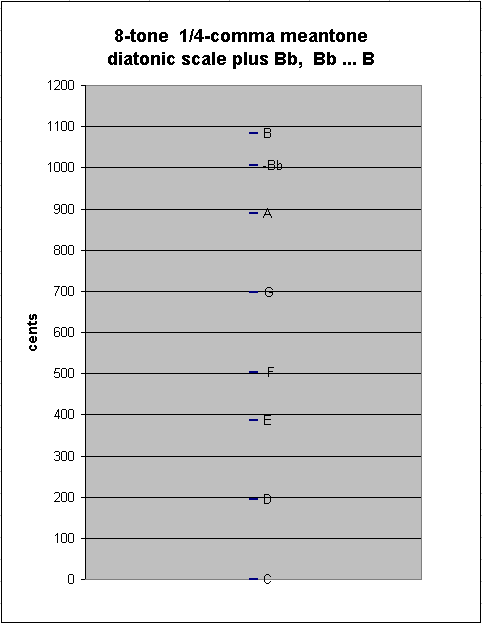
Introducing "Bb" into the scale causes a new between-degree interval to appear: the ~76.04899926-cent "chromatic semitone" between Bb:B :
generator 8ves 5 ~cents
5 -2 * [ 5/4] 1082.892142 "B"
-2 - 2 * [-2/4] 1006.843143 "Bb"
---------------------------
7 -4 * [ 7/4] 76.04899926 1/4-comma meantone chromatic semitone ("augmented prime")
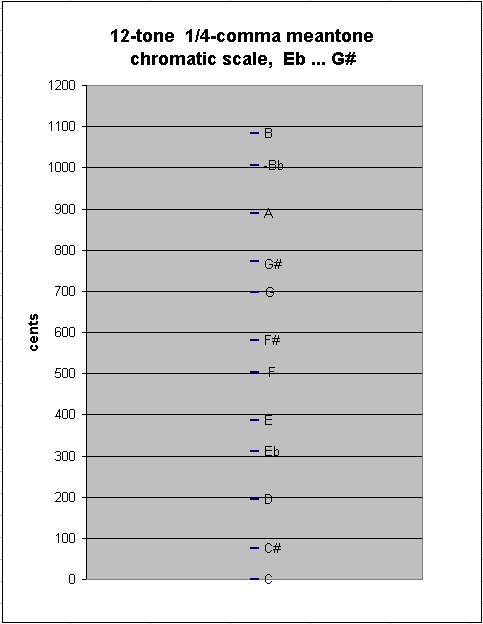
Continuing to add pitches at either end of the chain, we eventually come to the "typical" 12-tone chromatic scale used in Europe during the meantone era, from Eb to G#. This scale has as between-degree intervals only the two sizes of semitones, chromatic and diatonic:
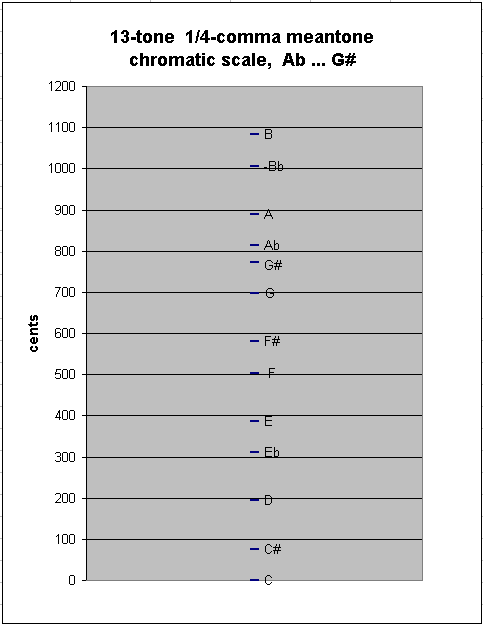
Adding one more note to either end results in another new between-degree interval, of ~41.05885841 cents, as between G#:Ab in my example here:
generator 8ves 5 ~cents
-4 3 * [ -4/4] 813.6862861 "Ab"
8 - -4 * [ 8/4] 772.6274277 "G#"
---------------------------
-12 7 * [-12/4] 41.05885841 2/7-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
It was fairly common during the 1600s and 1700s to find keyboards which had "split keys", so that "black keys" were actually pairs of keys giving both flats and sharps, which are separated by a diesis:
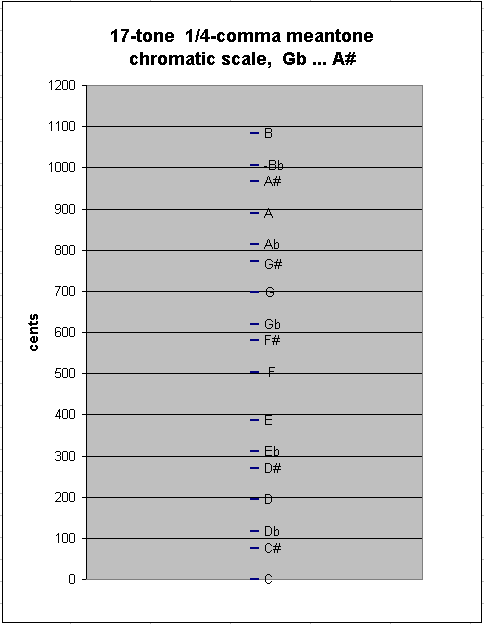
One may continue to add many more notes in this manner without encountering a new step-size; thus, the 19-tone chain of 1/4-comma meantone has between-degree intervals of ~41.05885841 and ~76.04899926 cents:
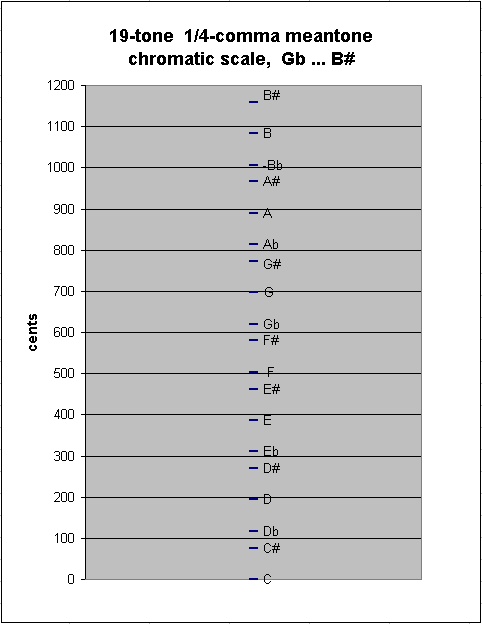
If one continues to add notes, eventually at the 31st note there will occur another smaller interval, as described below. Extend the chain, for example, to 14 pitches on the "flat" side of the origin and 17 on the "sharp" side, so that the -14th generator = "Cbb" and +17th generator = "Ax" :
generator 8ves 5 ~cents
-14 9 * [-14/4] 1047.902001 "Cbb"
17 - -9 * [ 17/4] 1041.833284 "Ax"
------------------------------
-31 18 * [-31/4] 6.068717548 (= ~6 1/15 cents) = 1/4-comma meantone "quadruply-diminished 3rd"
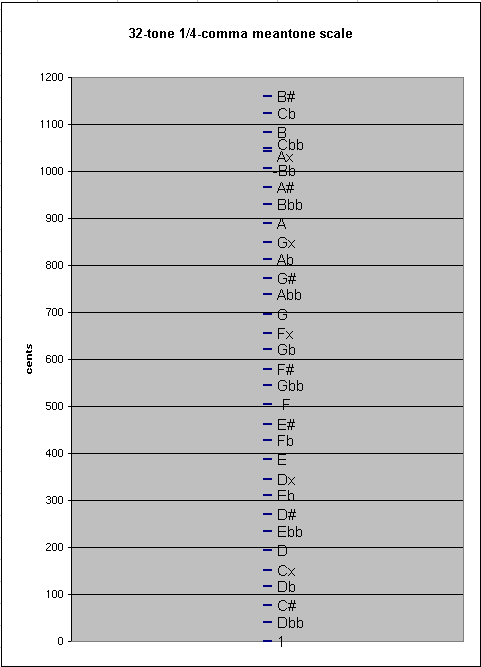
This is the 1/4-comma meantone interval of enharmonicity: in the example here, I assumed as system of -13 ...+17, and have added the -14th generator (it doesn't matter to which side, positive or negative, the extra generator is added -- the result is the same).
Thus, 218 * 5-(31/4) acts as a unison-vector which is not tempered out in 1/4-comma meantone, and it acts as a unison-vector which is tempered out in 31edo.
Below is a graph showing the pitch-height of this 32-tone chain of 1/4-comma meantone. The red line connects the two pitches which are close together.
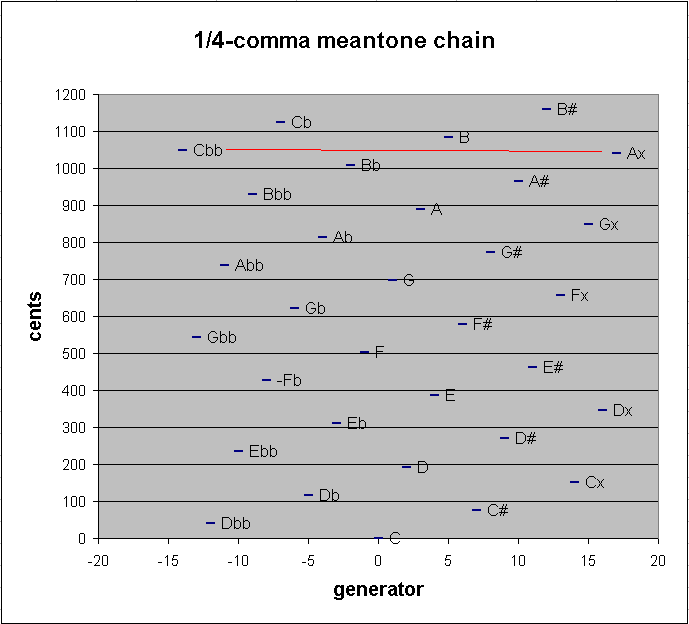
6.068717548 / 31 = 0.195765082 cents --> compare with above: this is the amount each
1/4-comma meantone generator must be tempered in order to acheive 31edo.
Below is a 2-dimensional
5-limit
bingo-card
lattice-diagram,
showing the
periodicity
of the 31edo representations of 5-limit
ratios,
with a typical spelling in a
chain from
Gbb at -13
generators
to Ax at +17 generators where C=n0
-- there is hardly any music in the
"common-practice (c. 1600-1900) repertoire which has
notes falling outside this range.
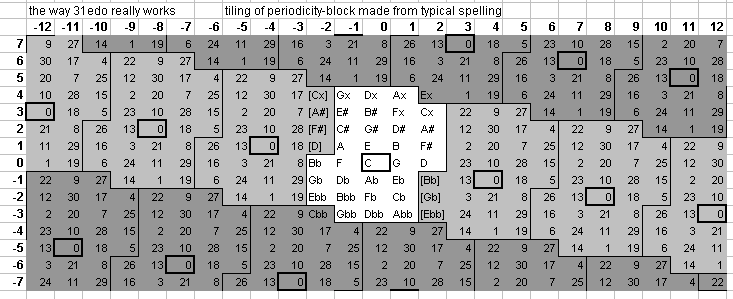
Exponents of 3 run across the top row and exponents of 5 run in a column down the left side; C n0 is outlined in heavy black; syntonic-comma equivalents (which have the same spelling) are in a light shade of grey; enharmonically equivalent pitches (which have a different spelling but are the same pitch as those in the central block) are in a darker shade of grey. Integers designate the degrees of 31edo.
For more commentary on 1/4-comma meantone and
31-EDO, see
Meantone tunings can be and have been extended to as many notes per 'octave' as desired, but when used for fretted strings or, especially, keyboards, they are usually limited to 12 discrete pitches per 'octave'.
Regardless of how many notes the meantone has, comparing any two notes which are inclusively 12 steps apart in the chain of "5ths" results in a 'wolf 5th' and its complementary 'wolf 4th', as can be seen in the following two tables. The 'wolves' occur between the '5th'/'4th' complementary pair which bound the notes at the end of the series of 12 '5ths'.
In the tables below, the reference pitch (1/1) is 'A', and the series of '5ths' runs arbitrarily from 3-6 (= 'Eb') to 35 (= G#). The first table is an interval matrix of all possible intervals between any two pitches in this tuning. The second table lists all available intervals and the notes between which they can be found.
interval sizes given in Semitones
'3x' indicates the implied '5th' in the
'cycle of 5ths', not the actual tuning
This is the most common mapping of meantone to a set of 12 pitch-classes, extending from Eb on the flat side to G# on the sharp side.
| G# | G | F# | F | E | Eb | D | C# | C | B | Bb | A | |||
| 3x | 5 | -2 | 3 | -4 | 1 | -6 | -1 | 4 | -3 | 2 | -5 | 0 | ||
| G# | 5 | 0.00 | 11.24 | 10.07 | 9.31 | 8.14 | 7.38 | 6.21 | 5.03 | 4.27 | 3.10 | 2.34 | 1.17 | |
| G | -2 | 0.76 | 0.00 | 10.83 | 10.07 | 8.90 | 8.14 | 6.97 | 5.79 | 5.03 | 3.86 | 3.10 | 1.93 | |
| F# | 3 | 1.93 | 1.17 | 0.00 | 11.24 | 10.07 | 9.31 | 8.14 | 6.97 | 6.21 | 5.03 | 4.27 | 3.10 | |
| F | -4 | 2.69 | 1.93 | 0.76 | 0.00 | 10.83 | 10.07 | 8.90 | 7.73 | 6.97 | 5.79 | 5.03 | 3.86 | |
| E | 1 | 3.86 | 3.10 | 1.93 | 1.17 | 0.00 | 11.24 | 10.07 | 8.90 | 8.14 | 6.97 | 6.21 | 5.03 | |
| Eb | -6 | 4.62 | 3.86 | 2.69 | 1.93 | 0.76 | 0.00 | 10.83 | 9.66 | 8.90 | 7.73 | 6.97 | 5.79 | |
| D | -1 | 5.79 | 5.03 | 3.86 | 3.10 | 1.93 | 1.17 | 0.00 | 10.83 | 10.07 | 8.90 | 8.14 | 6.97 | |
| C# | 4 | 6.97 | 6.21 | 5.03 | 4.27 | 3.10 | 2.34 | 1.17 | 0.00 | 11.24 | 10.07 | 9.31 | 8.14 | |
| C | -3 | 7.73 | 6.97 | 5.79 | 5.03 | 3.86 | 3.10 | 1.93 | 0.76 | 0.00 | 10.83 | 10.07 | 8.90 | |
| B | 2 | 8.90 | 8.14 | 6.97 | 6.21 | 5.03 | 4.27 | 3.10 | 1.93 | 1.17 | 0.00 | 11.24 | 10.07 | |
| Bb | -5 | 9.66 | 8.90 | 7.73 | 6.97 | 5.79 | 5.03 | 3.86 | 2.69 | 1.93 | 0.76 | 0.00 | 10.83 | |
| A | 0 | 10.83 | 10.07 | 8.90 | 8.14 | 6.97 | 6.21 | 5.03 | 3.86 | 3.10 | 1.93 | 1.17 | 0.00 |
List of Intervals of 12-tone 1/4-comma meantone
(same mapping as that used above)
| interval | generators | Semitones | 31edo degrees | instances | |||||||||||
| diminished 8ve | -7 | 11.24 | 29 | G#:G | F#:F | E:Eb | C#:C | B:Bb | |||||||
| major 7th | +5 | 10.83 | 28 | G:F# | F:E | Eb:D | D:C# | C:B | Bb:A | A:G# | |||||
| minor 7th | -2 | 10.07 | 26 | G#:F# | G:F | F#:E | F:Eb | E:D | D:C | C#:B | C:Bb | B:A | A:G | ||
| augmented 6th | +10 | 9.66 | 25 | Eb:C# | Bb:G# | ||||||||||
| diminshed 7th | -9 | 9.31 | 24 | G#:F | F#:Eb | C#:Bb | |||||||||
| major 6th | +3 | 8.90 | 23 | G:E | F:D | E:C# | Eb:C | D:B | C:A | B:G# | Bb:G | A:F# | |||
| minor 6th | -4 | 8.14 | 21 | G#:E | G:Eb | F#:D | E:C | D:B | C#:A | B:G | A:F | ||||
| augmented 5th | +8 | 7.73 | 20 | F:C# | Eb:B | C:G# | Bb:F# | ||||||||
| wolf 5th | -11 | 7.38 | 19 | G#:Eb | |||||||||||
| 'perfect' 5th | +1 | 6.97 | 18 | G:D | F#:C# | F:C | E:B | Eb:Bb | D:A | C#:G# | C:G | B:F# | Bb:F | A:E | |
| diminished 5th | -6 | 6.21 | 16 | G#:D | F#:C | E:Bb | C#:G | B:F | A:Eb | ||||||
| augmented 4th | +6 | 5.79 | 15 | G:C# | F:B | Eb:A | D:G# | C:F# | Bb:E | ||||||
| 'perfect' 4th | -1 | 5.03 | 13 | G#:C# | G:C | F#:B | F:Bb | E:A | D:G | C#:F# | C:F | B:E | Bb:Eb | A:D | |
| wolf 4th | +11 | 4.62 | 12 | Eb:G# | |||||||||||
| diminished 4th | -8 | 4.27 | 11 | G#:C | F#:Bb | C#:F | B:Eb | ||||||||
| major 3rd | +4 | 3.86 | 10 | G:B | F:A | E:G# | Eb:G | D:F# | C:E | Bb:D | A:C# | ||||
| minor 3rd | -3 | 3.10 | 8 | G#:B | G:Bb | F#:A | E:G | D:F | C#:E | C:Eb | B:D | A:C | |||
| augmented 2nd | +9 | 2.69 | 7 | F:G# | Eb:F# | Bb:C# | |||||||||
| diminished 3rd | -10 | 2.34 | 6 | G#:Bb | C#:Eb | ||||||||||
| major 2nd | +2 | 1.93 | 5 | G:A | F#:G# | F:G | E:F# | Eb:F | D:E | C:D | B:C# | Bb:C | A:B | ||
| minor 2nd | -5 | 1.17 | 3 | G#:A | F#:G | E:F | D:Eb | C#:D | B:C | A:Bb | |||||
| augmented unison | +7 | 0.76 | 2 | G:G# | F:F# | Eb:E | C:C# | Bb:B | |||||||
| unison / 8ve | 0 | 0 or 12 | 0 | G#:G# | G:G | F#:F# | F:F | E:E | Eb:Eb | D:D | C#:C# | C:C | B:B | Bb:Bb | A:A |
It can be seen that a 12-tone subset of meantone contains at least one instance of all intervals from -11 to +11 generators.
Use of certain meantone chords may have been the result of their resemblance to certain basic JI sonorities, for example, the "augmented-6th" (+10 generators) is a close approximation of the 7th harmonic (7:4 ratio).
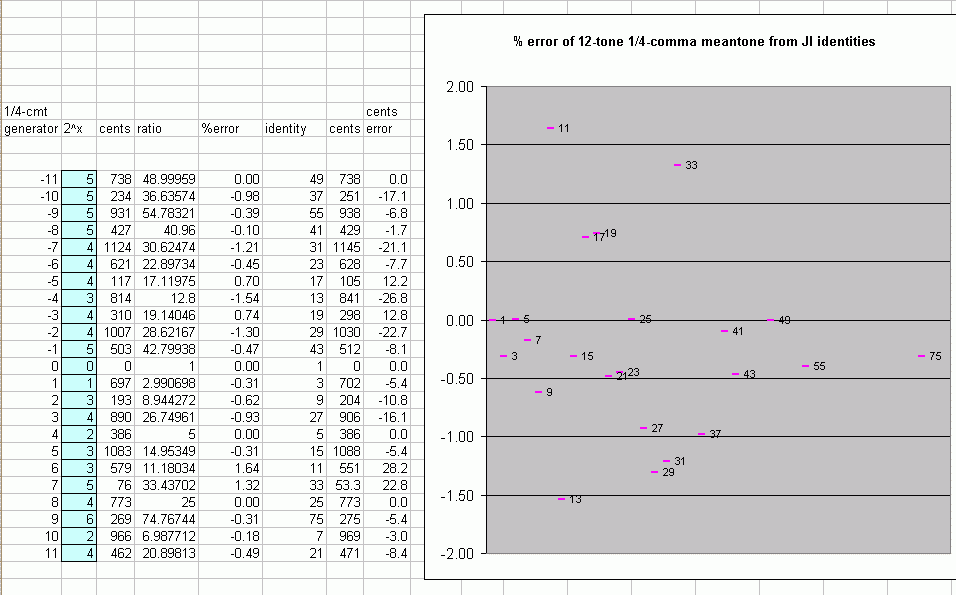
Below is a table and graph showing how closely the intervals in the 12-tone subset of 1/4-comma meantone given above approximate JI chord identities.
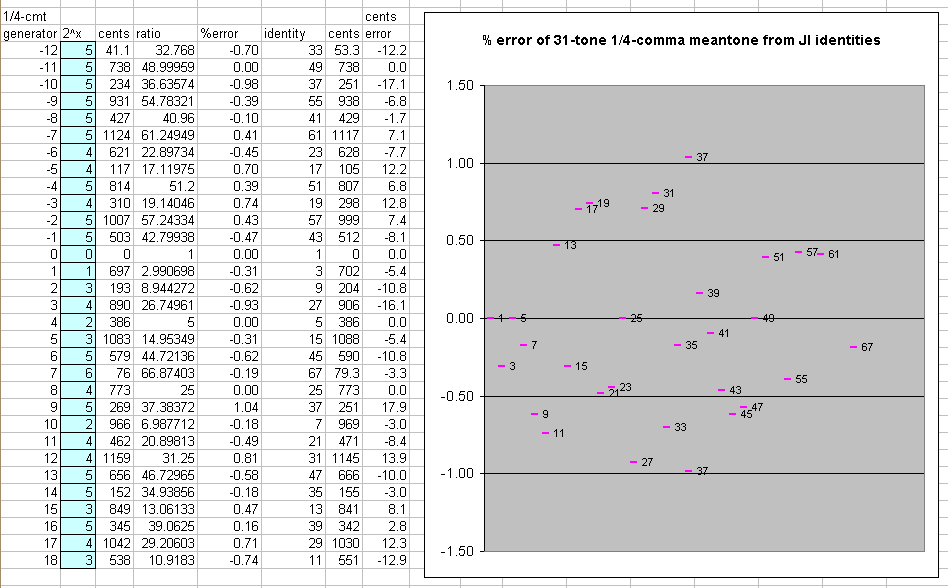
Below is a table and graph showing how closely a 31-tone set of 1/4-comma meantone approximates JI chord identities.
Here is a graph comparing 1/4-comma meantone with Werckmeister III tuning:

in http://groups.yahoo.com/group/tuning/message/8553 Margo Schulter writes:
'Aaron, writing an introduction to music in Italian (_Toscanello_ is a title honoring his native Tuscany), advises the not necessarily experienced reader to start by making the octave C-C "just," and then the major third C-E "sonorous and just, as united as possible." While Aaron does not specify a pure 5:4 for the major third, this seems to me a natural reading of "sonorous and just." Then the fifths C-G-D-A-E are tuned so that each is slightly "flat" or "lacking," and each by the same amount. For example, A should be the same "distance" from D as from E -- in other words, the fifths D-A and A-E should be tempered from "perfection" by the same quantity.
As far as I'm concerned, this is enough to justify listing Aaron's instructions as a description the procedure for obtaining 1/4-comma meantone -- as various authors have done, and Paul does in his table. Further, Aaron adds after his C-G-D-A-E series of fifths that F should be tuned by a similar but opposite procedure, making F in the fifth F-C "a little high, passing a bit beyond perfection." If one assumes symmetry, then 1/4-comma meantone indeed results.
Correctly pointing out that Aaron's instructions do not give a mathematical description of 1/4-comma meantone, or explicitly direct that all major thirds be made pure, Lindley raises the question of what Aaron means by his statement that "thirds and sixths are blunted or diminished" in this temperament.
One interpretation which occurs to me is that Aaron is comparing meantone _major_ thirds and sixths with the same intervals in a Pythagorean tuning with pure fifths -- where they are indeed somewhat larger. Lindley emphasizes such ambiguous statements to argue that Aaron's instructions do specify 1/4-comma for the first notes C-G-D-A-E, but might lend themselves to various slightly irregular tunings for the other fifths and thirds.
Another point made by Lindley is that Aaron uses the adjective _giusta_ ("just") to refer not only to his initial octave and major third (where "pure" is an attractive reading), but also for the temperament as a whole -- _participatione & acordo giusto & buono_, "a just and good temperament and tuning." However, Lindley himself is ready to accept Aaron's opening C-G-D-A-E with its "sonorous and just" major third C-E as a description of 1/4-comma. His statement about the octave C-C and major third C-E being as sonorous or "united" as possible would support this conclusion even we assume that "just" may mean simply "euphonious" or "pleasing."
In his instructions for the final stage of the temperament, the tuning of the sharps, Aaron directs that C#, tuned in relation to the fifth A-E, should be a major third from A and a minor third from E, and likewise with F# in relation to the fifth D-A, etc.
From one viewpoint, this language may simply be reminding the student of the locations of major and minor thirds involving accidentals. Lindley, however, pursuing his argument that a regular 1/4-comma temperament is not _necessarily_ implied, argues that one _could_ read this language to suggest something like Zarlino's 2/7-comma meantone for the temperament of the sharps, with major and minor thirds compromised by about the same amount from pure.
In arguing that Aaron's tuning is not _necessarily_ a regular 1/4-comma meantone, Lindley may have two motivations. First, he wishes to emphasize that Aaron's instructions are not mathematically precise; and indeed, I would agree that Zarlino (1571) and Salinas (1577) may be the first known theorists to give such mathematical definitions of 1/4-comma and other meantone temperaments.
Secondly, Lindley wants to correct the view that 1/4-comma was a universal standard in the 16th century. Since Aaron's instructions are often taken as the paradigm case of this tuning, showing that they are actually open to more than one interpretation would fit with his larger campaign against "1/4-comma hegemony."
However, I find it noteworthy that without invoking any complex mathematical concepts or even defining a syntonic comma, Aaron has described in what I find beautiful as well as musicianly terms the idea of tuning a pure major third and then dividing it into four equally tempered fifths. Aaron's remaining instructions, including his suggestion of a similar but opposite tempering of fifths in the flat direction (F-C, and then Bb-F and Eb-Bb), permit a regular 1/4-comma temperament, even if they do not compel it or define it in mathematical terms.
If I were making a table like Paul's, I might list Aaron for 1/4-comma and add a footnote or annotation like this:
"Aaron evidently describes a temperament with a pure major third C-E and equally narrowed fifths for his first five notes C-G-D-A-E, with further instructions permitting but not explicitly specifying that other major thirds are pure; Zarlino (1571) and Salinas (1577) give mathematically precise descriptions of a regular 1/4-comma tuning."'
Updated:
2003.03.30 -- added pitch-height graphs showing expansion to 32-tone chain
2003.03.17 -- added corrections near the top of the page, suggested by paul erlich
2003.03.13 -- added long quote from Margo Schulter at end (thanks to paul erlich)
2003.01.30 -- added graph comparing 1/4-comma meantone with Werckmeister III
2002.11.7 -- added table of approximations to JI chord identities
2002.10.25 -- added bingo-card lattice of typical 31-tone chain, and 31edo-degrees in interval list
2002.09.24 -- added historical comments, and math to show "mean tone" and "major 3rd" derivations
2001.11.05
2001.06.26
2000.08.10
by Joe Monzo
|
(to download a zip file of the entire Dictionary, click here) |
|
|