- For many more diagrams and explanations of historical tunings, see
my book.
- If you don't understand my theory or the terms I've used, start here
All meantone tunings contain subsets which are diatonic scales consisting of two different "step" sizes, designated L and s.
In 31edo, the large interval (L), the "whole-step" or
"whole-tone",
the interval of a "major 2nd", is:
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
G [ 0 +1] 1.495517882 696.7741935 18
- F [+1 -1] ÷ 1.337329378 - 503.2258065 13
------------- ------------- --------------- ---
* [-1 +2] 1.118286868 193.5483871 5
* This always results in a change of letter-name.
This is the "mean-tone" which occurs almost exactly midway between the two JI "whole-tones" with ratios of 10:9 and 9:8. (The exact mean-tone is that of 1/4-comma meantone.)
The small interval (s), "half-step",
which is also the
diatonic
semitone
and the interval of a "minor 2nd", is:
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
F [+1 -1] 1.337329378 503.2258065 13
- E [-2 +4] ÷ 1.25056552 - 387.0967742 10
------------- ------------- --------------- ---
* [+3 -5] 1.069379699 116.1290323 3
* This always results in a change of letter-name.
In both historical chronology and the method of
scale construction by generators, the
chromatic
semitone first emerges in meantone as the
interval between B and Bb:
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Bb [+2 -2] 1.788449866 1006.451613 26
- B [-2 +5] ÷ 1.870243098 - 1083.870968 28
------------- ------------- --------------- ---
b [+4 -7] 0.956265989 -77.41935484 29 = -2 mod 31
The "round-b" or "soft-b" was used to notate Bb, and eventually evolved into the "flat" symbol, defined as above. This signifies a flattening by 2 degrees of 31edo.
B-natural was notated as "square-b" or "hard-b".
Gradually, as the scale was extended, this "square-b"
evolved into both the "natural" and "sharp" symbols,
and also resulted in the Eastern European practice
of calling "B-flat" simply "b", and
"B-natural" is "h".
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
F# [-3 +6] 1.398490998 580.6451613 15
- F [+1 -1] ÷ 1.337329378 - 503.2258065 13
------------- ------------- --------------- ---
# [-4 +7] 1.045734148 +77.41935484 2
This is the interval of the "augmented unison" or "augmented prime", and signifies a sharpening by 2 degrees of 31edo.
Extending the system still further, to Eb -3 on the flat
side and to D# +9 on the sharp side, we find a smaller
interval, the "diminished 2nd":
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Eb [+2 -3] 1.195873274 309.6774194 8
- D# [-5 +9] ÷ 1.169430766 - 270.9677419 7
------------- ------------- --------------- ---
[+7 -12] 1.022611436 38.70967742 1
Extending the system still further, to Cb -7 on the flat
side and to B# +12 on the sharp side, we find a new interval,
the "augmented 7th" minus an "8ve",
which is exactly the same size as that discovered above:
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
B# [ -6 +12] 1.95577707 1161.290323 30
- Cb [ +5 -7] ÷ 1.912531979 - 1122.580645 29
-------------- ------------- ---------------- ---
[-11 +19] 1.022611436 38.70967742 1
Finally, extending the system to Cbb -14 on the flat
side and Ax +17 on the sharp side, we find the point
where the system closes:
C = n0
8ve gen ~ratio ~cents 31edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Cbb [ +9 -14] 1.828889285 1045.16129 27
- Ax [ -9 +17] ÷ 1.828889285 - 1045.16129 27
--------------- ------------- ------------ ---
[+18 -31] 1 0 0
Below is a 2-dimensional
5-limit
bingo-card
lattice-diagram,
showing the
periodicity
of the 31edo representations of 5-limit
ratios,
with a typical spelling in a
chain from
Gbb at -13
generators
to Ax at +17 generators where C=n0
-- it would be difficult to find music from the
"common-practice" (c. 1600-1900) repertoire which has
notes falling outside this range.
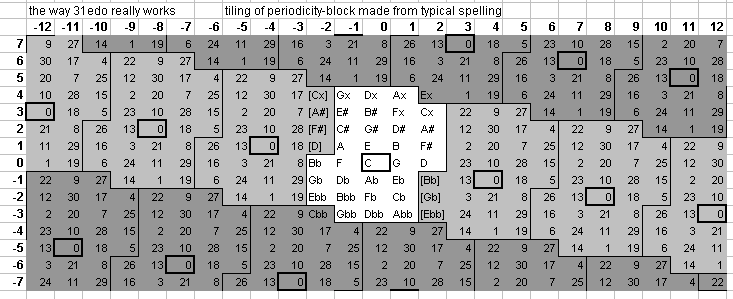
Exponents of 3 run across the top row and exponents of 5 run in a column down the left side; C n0 is outlined in heavy black; syntonic-comma equivalents (which have the same spelling) are in a light shade of grey; enharmonically equivalent pitches (which have a different spelling but are the same pitch as those in the central block) are in a darker shade of grey. Integers designate the degrees of 31edo.
Updated:
2002.10.25 -- added bingo-card-lattice of typical 31-tone spelling, and 31edo tabulations of intervals
2002.09.30 -- page created
by Joe Monzo
-->
|
(to download a zip file of the entire Dictionary, click here) |
|
|