- blackjack,
- canasta,
- my Blackjack webpage,
- Dave Keenan's circular MIRACLE graph, and
- Graham Breed's decimal notation.
A notation invented by Graham Breed for representing the MIRACLE family of tunings.
The notation is based on the fact that the MIRACLE generator produces 10- and 11-tone MOSs in which the 11th tone is audibly quite close to the origin tone.
Graham's own webpages describe the decimal notation itself, and the decimal lattices which use it.
Below is an explanatory elaboration based on a post I sent to the tuning list.
> ----- Original Message -----
Here's a real quick stab at it, Joe... but it should help.
Secondly, realize that Graham's notation is generalized in
that it is applicable to 31- and
41-EDO as well as
72-EDO.
I'm going to discuss it here only in terms of 72-EDO.
Now look at the "melodic" description of Graham's notation in
the first section of
his
webpage.
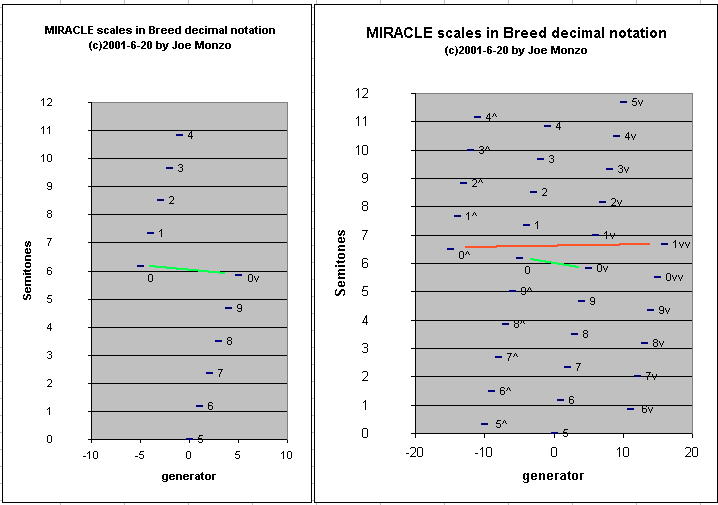
Here's a list of the basic 10-tone MIRACLE scale, in descending
order (as usual with me... sorry Dave Keenan...), with Graham's
"s" and "q" interval-spacing:
So as Graham explains, "s" in 72-EDO MIRACLE is 2(7/72),
and "q" is the new interval we find at 11 tones, which is
2(2/72). So the large interval at the end of the 10-tone
cycle is "s+q" = 2(9/72).
Graham's notation uses "v" and "^" as accidentals, in which
"the ^ and v symbols denote upward and downward shifts of q".
So if we decide to include that 11th tone of
5 5/6 Semitones,
which is the +5 generator, it would be called 0v, which indicates
that the origin, 6 1/6
Semitones, has been flattened by "q",
which is 2(2/72) = 33 1/3
cents = 1/3 Semitone =
"1/6-tone":
Here are my graphs of Graham's notation, for both the
11-tone and 32-tone MIRACLE cycles:
So now look at the 32-tone MIRACLE graph, and notice how
all subsequent pitches added to our
gamut will be described
in terms of the basic 10-tone scale tabulated above.
So if we continue the cycle on the positive side, adding
the +6 generator = 7 Semitones, it would be "1v", which is:
and so on.
If we continue on the negative side, adding the -6 generator
= 5 Semitones, it would be "9^", which is:
and so on.
The -15 generator = 6 1/2
Semitones would be "0^", because
it is one "q" higher than our origin note "0":
The -16 generator would be "9^^", because it is one "q" higher
than "9^".
On the positive side, the +15 generator = 5&1/2 Semitones
would be "0vv", because it is one "q" lower than "0v":
The +16 generator = 6 2/3
Semitones would be "1vv", because
it is one "q" lower than "1v":
Note, however, that this "1vv" is
1/2 "q" higher than "0^".
We've run up against the next level of
enharmonicity, which
delimits the
Canasta scale.
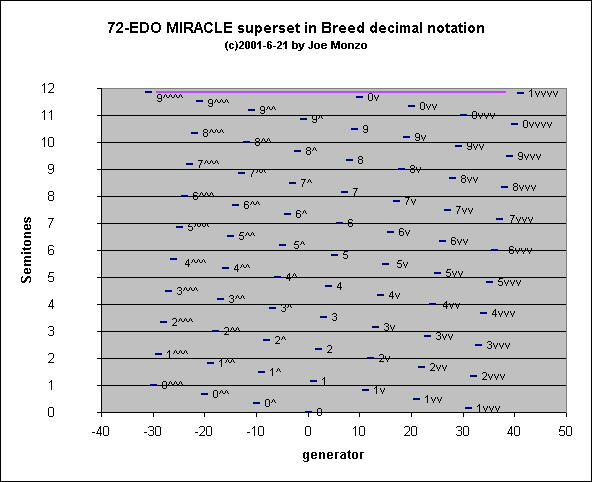
Below is a graph of the entire 72-EDO superset in Graham's
decimal notation. I've used a different starting point
for the decimal nominals here, calling the 0 generator
also the 0 nominal, to conform with the usage on Graham's webpage.
A purple line connects the -31 and +41 generators, which
give exactly the same pitch, thus closing the cycle at 72 tones.
9^^^^ and 1vvvv are thus
enharmonically equivalent
in this notation.
[from Joe Monzo, JustMusic:
A New Harmony]
> From:
> To:
> Sent: Thursday, June 21, 2001 6:11 AM
> Subject: [tuning] Re: updated "MIRACLE" definition webpage
>
>
> > Now, could I please ask you to elaborate a bit on Graham Breed's
> > decimal notation, so I can understand it??
First of all, realize that Graham's use of numbers here is
exactly equivalent to the way we currently use the first seven
letters of the alphabet to describe the 7-tone diatonic cardinality.
So the digits 0 ... 9 are the 10-tone cardinality of the basic
MIRACLE scale.
OK, now look at the
graph
of the 11-tone MIRACLE scale
(the one with the green line) on my MIRACLE definition
webpage. Keep this window open or print it out... you'll be
using my two recent graphs a lot in following what I say here.
Let's start the scale at the -5 generator, giving the pitch
which is 6&1/6
Semitones,
which we will call "0". We are
considering Graham's 10-tone scale here, not the 11-tone one
I illustrate. So here the +5 generator, giving the pitch at
5&5/6 Semitones, which is the one close to the origin, will be
omitted. So we'll use as our bounding notes the -5 and +4 generators.
Generator Graham's Semitones interval between
"note" Semitones 72-EDO-degrees
-5 0 6 1/6
> 1 1/2 9 s+q
+4 9 4 2/3
> 1 1/6 7 s
+3 8 3 1/2
> 1 1/6 7 s
+2 7 2 1/3
> 1 1/6 7 s
+1 6 1 1/6
> 1 1/6 7 s
0 5 0
> 1 1/6 7 s
-1 4 10 5/6
> 1 1/6 7 s
-2 3 9 2/3
> 1 1/6 7 s
-3 2 8 1/2
> 1 1/6 7 s
-4 1 7 1/3
> 1 1/6 7 s
-5 0 6 1/6
"0" - "q" = "0v"
6 1/6 Semitones - 1/3 Semitone = 5 5/6 Semitones
"1" - "q" = "1v"
7 1/3 Semitones - 1/3 Semitone = 7 Semitones
"9" + "q" = "9^"
4 2/3 Semitones + 1/3 Semitone = 5 Semitones
"0" + "q" = "0^"
6 1/6 Semitones + 1/3 Semitone = 6 1/2 Semitones
"0v" - "q" = "0vv"
5 5/6 Semitones - 1/3 Semitone = 5 1/2 Semitones
"1v" - "q" = "1vv"
7 Semitones - 1/3 Semitone = 6 2/3 Semitones
See also:
2002.09.27 -- reformatted all fractions
2002.09.23 -- reformatted fonts of tables
2001.06.27