An early and very simple proposal for a meantone tuning was 1/3-comma meantone and its close relative 19edo. The earliest alleged use of this tuning is by Guillaume Costeley in 1558, in his chanson Seigneur Dieu ta pitiť. The most well-known early reference, to both tunings, was by Salinas in 1577.
The 1/3-comma meantone "5th" -- the
generator --
is (3/2) / ((81/80)(1/3)). Using
vector addition,
that's:
2^ 3^ 5^
[ -1 1 0 ] = Pythagorean ("pure") "perfect 5th" of 3:2 ratio
- [ -4/3 4/3 -1/3 ] = (2-4345-1)(1/3) = (81/80)(1/3)
-----------------------
[ 1/3 -1/3 1/3 ] = 1/3-comma meantone "5th"
= ~694.7862377 cents.
This has the effect of
tempering out the
syntonic comma so
that it vanishes, thus making 4 "5ths" minus 2 "8ves"
fairly close to the
just
"major 3rd":
2^ 3^ 5^
[ 4/3 -4/3 4/3 ] = 4 1/3-comma meantone "5ths"
- [ 2 0 0 ] = 2 "8ves"
-----------------------
[ -2/3 -4/3 4/3 ] = 1/3-comma meantone "major 3rd" = ~379.1449507 cents.
the difference between the JI and the 19edo "major-3rds" is:
2^ 3^ 5^
[ -2/3 -4/3 4/3 ] = 1/3-comma meantone "major 3rd"
- [ -2 0 1 ] = JI "major 3rd" of 5:4 ratio
-----------------------
[ 4/3 -4/3 1/3 ] = error of 19edo from JI "major-3rd" = - ~7.168763 cents.
This amount is exactly 1/3 of a syntonic comma.
Assuming "octave"-equivalence
(i.e., the exponents of 2 are irrelevant to the construction of the
scale, so i've added 2-2 to the
vector here to put
the note into the reference "octave"),
the next note in the cycle after the "5th", that of
+2 generators,
is the "whole-tone"
2(2/3) 3-(2/3) 5(2/3) = ~189.5724753
cents. If we compare
this to the two JI
"whole-tones", subtracting the meantone from the larger
Pythagorean 9/8
and subtracting the smaller
5-limit 10/9
from the meantone, we find where the meantone lies between
the two JI "whole-tones":
2^ 3^ 5^
[ -3 2 0 ] = 9/8
- [ 2/3 -2/3 2/3 ] = 1/3-comma meantone
-----------------------
[ -2 2 -2/4 ] = ~14.3375264 cents = exactly 2/3-comma smaller than 9/8.
2^ 3^ 5^
[ 2/3 -2/3 2/3 ] = meantone
- [ 1 -2 1 ] = 10/9
-----------------------
[ -1/3 4/3 -1/3 ] = ~7.168763199 cents = exactly 1/3-comma larger than 10/9.
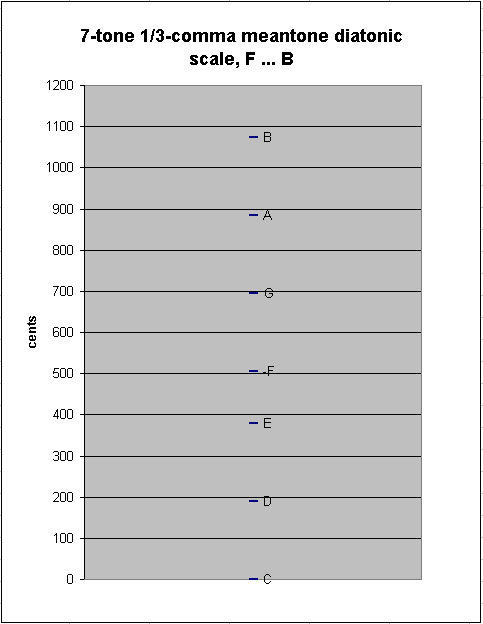
The 7-tone diatonic scale in 1/3-comma meantone contains only two "step" sizes: the ~189.5724753-cent "whole-tone" described above, between C:D, D:E, F:G, G:A, and A:B, and the ~126.0688117-cent "diatonic semitone" between E:F and B:C:
generator 8ves 2 3 5 ~cents
-1 1 * [-1/3 1/3 -1/3] 505.2137623 "F"
4 - -2 * [ 4/3 -4/3 4/3] 379.1449507 "E"
---------------------------
-5 3 * [-5/3 5/3 -5/3] 126.0688117 1/3-comma meantone diatonic semitone ("minor-2nd")
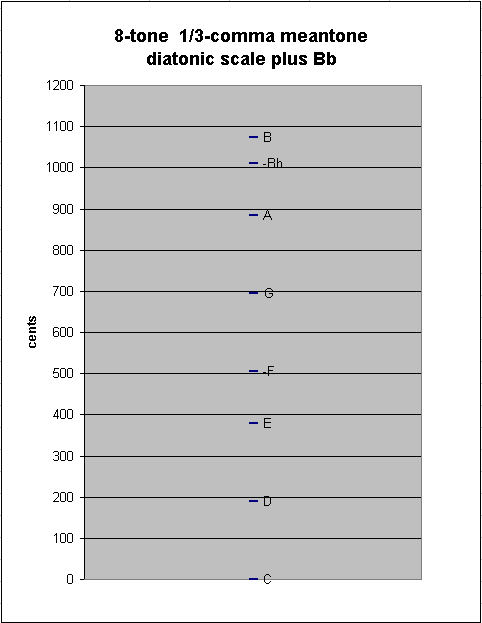
Introducing "Bb" into the scale causes a new between-degree interval to appear: the ~63.50366367-cent "chromatic semitone" between Bb:B :
generator 8ves 2 3 5 ~cents
5 -2 * [ 5/3 -5/3 5/3] 1073.931188 "B"
-2 - 2 * [-2/3 2/3 -2/3] 1010.427525 "Bb"
---------------------------
7 -4 * [ 7/3 -7/3 7/3] 63.50366367 1/3-comma meantone chromatic semitone ("augmented prime")
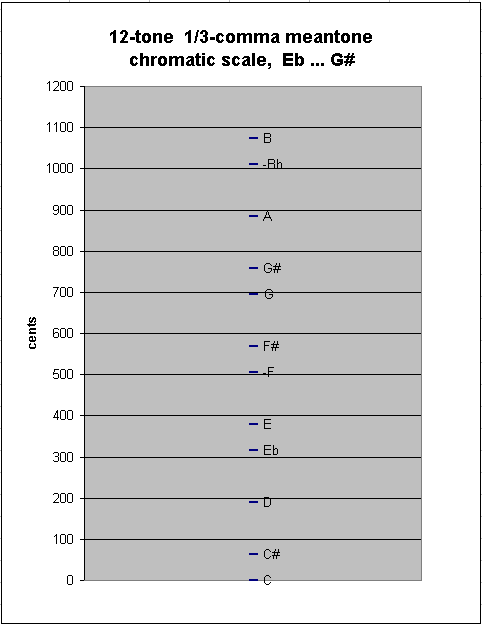
Continuing to add pitches at either end of the chain, we eventually come to the "typical" 12-tone chromatic scale used in Europe during the meantone era, from Eb to G#. This scale has as between-degree intervals only the two sizes of semitones, chromatic and diatonic:
Adding one more note to either end results in another new between-degree interval, of ~62.565148 cents, as between G#:Ab in my example here:
generator 8ves 2 3 5 ~cents
-4 3 * [ -4/3 4/3 -4/3] 820.8550493 "Ab"
8 - -4 * [ 8/3 -8/3 8/3] 758.2899013 "G#"
---------------------------
-12 7 * [-12/3 12/3 -12/3] 62.565148 1/3-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
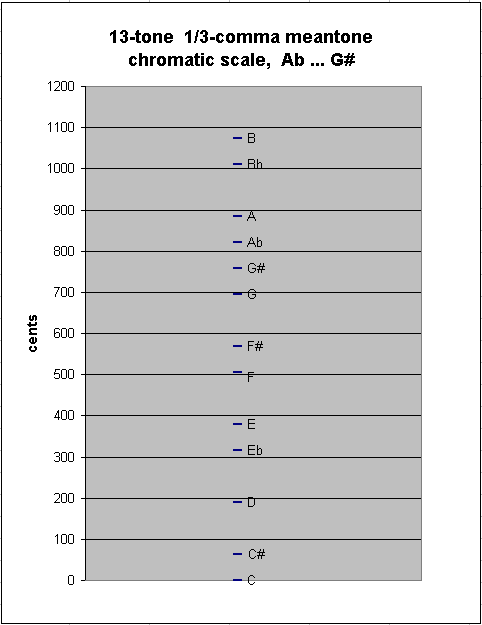
It can be seen both from the numbers and from the graph that this interval is almost the same size as the last one derived; thus, there is essentially no difference in 1/3-comma meantone between the chromatic semitone and the enharmonic diesis (-- and in 19edo, they do in fact become the same size) :
generator 8ves 2 3 5 ~cents
7 -4 * [ 7/3 -7/3 7/3] 63.50366367 1/3-comma meantone chromatic semitone ("augmented prime")
-12 - 7 * [-12/3 12/3 -12/3] 62.565148 1/3-comma meantone "great" (enharmonic) diesis ("diminished-2nd")
---------------------------
19 -11 * [ 19/3 -19/3 19/3] 0.938515663 1/3-comma meantone "small diesis" ("magic comma")
One may continue to add 6 more notes in this manner without encountering a step-size which is radically different, thus because of the similarity of the 1/3-comma meantone chromatic semitone and enharmonic diesis, the division of the "8ve" tends to become evened-out:

It can be seen from the graph directly above that this divides the "8ve" into 19 nearly-identical steps, and so it can be easily inferred that other new notes will be quite similar to those already produced, and that the system is thus in effect closed at 19 notes.
If a 20th note is added, for example -7 (Cb), there occurs a new, tiny between-degree interval, which is in fact the same "small diesis" calculated above: ~0.938515663 (= ~15/16) cent, ocurring between Cb and B# :
generator 8ves 2 3 5 ~cents
12 -6 * [12/3 -12/3 12/3] 1137.434852 "B#"
-7 - 5 * [-7/3 7/3 -7/3] 1136.496336 "Cb"
---------------------------
19 -11 * [19/3 -19/3 19/3] 0.938515663 1/3-comma meantone small diesis ("magic comma")
For all intents and purposes, this difference may be disregarded, so that 19edo can be considered identical to a 19-tone chain of 1/3-comma meantone. ~0.938515663 / 19 = ~0.049395561 cent: this miniscule amount is the difference between the 1/3-comma meantone "5th" and the 19edo "5th".

Below is a graph showing the pitch-height of this 20-tone chain of 1/3-comma meantone. The red line connects the two pitches which are close together.
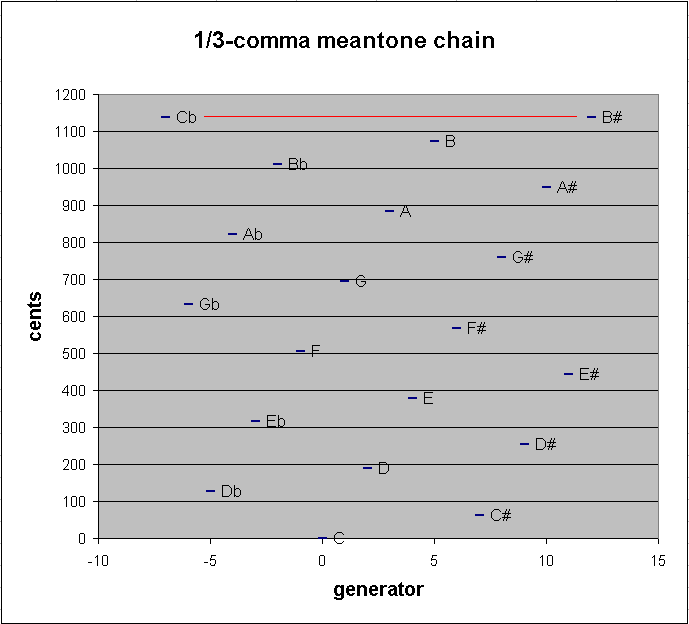
19-EDO
is audibly indistinguishable from 1/3-comma meantone.
2(11/19) = 696.7741935 cents.
Using vector addition again to compare the 1/3-comma meantone "5th"
with the 19-EDO "5th", we get a difference between the two of:
2^ 3^ 5^
[ 1/3 -1/3 1/3 ] = ~694.7862377 cents = 1/3-comma meantone "5th"
- [ 11/19 0 0 ] = ~694.7368421 cents = 19-EDO "5th"
-----------------------
[ -14/57 -1/3 1/3 ] = 19edo "5th" "-" 1/3-comma meantone "5th"
= ~0.049395561 cent = ~1/20 cent
Thus, 2(19/3) * 3-(19/3) * 5(19/3) acts as a unison-vector which is not tempered out in 1/3-comma meantone, and it acts as a unison-vector which is tempered out in 19edo. Because this interval is so small, it really makes no difference whether or not it is "officially" tempered out: it will sound like a unison in either case.
Salinas in 1577 (De Musica, book 3, chapter 16)
described 1/3-comma meantone with mathematical
exactitude for the first time.
First he constructed a 24-tone JI system, which had duplicate pairs of some pitches a syntonic comma apart, the higher of which was labeled "superius" and the lower "inferius".
Then he explained the amount of tempering for each of the meantone pitches. By tempering out the full comma which exists between the 5 pairs of "superius/inferius" pitches, he reduced the number of pitches from 24 to 19.
Below is a lattice which places Salinas's 1/3-comma meantone in prime-space and shows its relationship to his JI system, as he describes it; the slanted arrows represent the syntonic-comma:
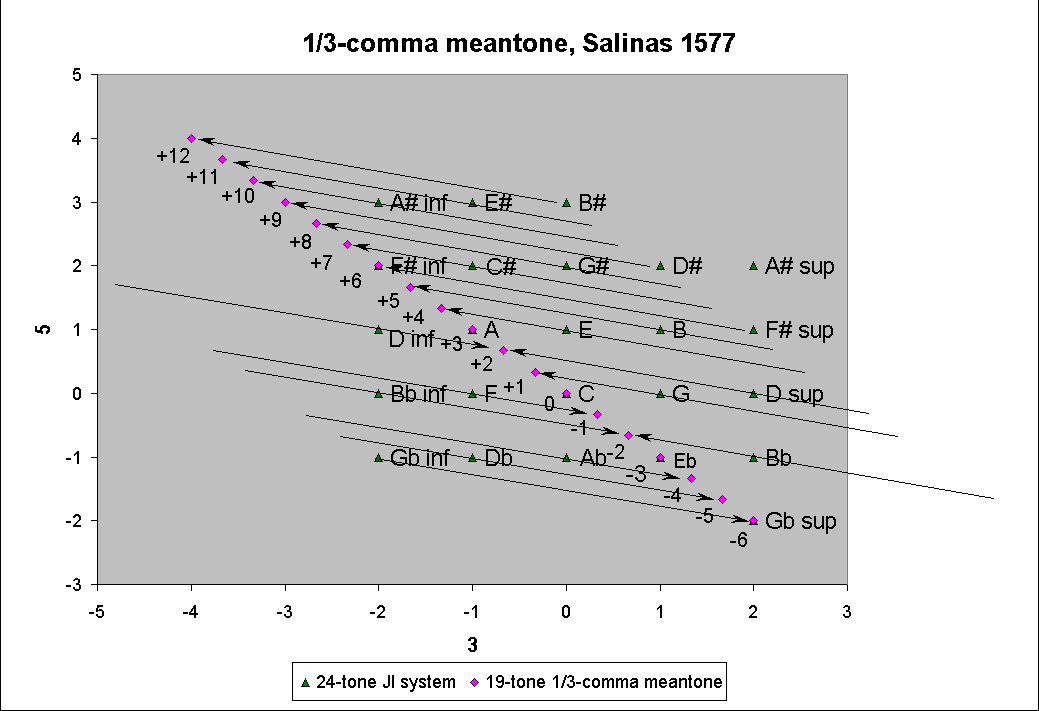
It can be seen that all pitches of the meantone are
either exactly those of Salinas's JI system, or are
1/3, 2/3, or a full comma higher or lower than
those in his JI system.
He goes on to explain how to temper the 24-note JI system into 19 notes of 2/7-comma meantone, and then also into 19 notes of 1/4-comma meantone, the latter of which he finally declares to be the best of the three temperaments.
Salinas did not explicitly mention the equal nature of the 8ve-division in his 1/3-comma meantone, but he would have known about it himself and it can be inferred from the measurements he described. The 19-tone systems of the 2/7-comma and 1/4-comma meantone are less equally-spaced, being rather closer to subsets of 50edo and 31edo, respectively.
Updated:
2003.03.30 -- page created
2003.03.31 -- Salinas diagram and commentary added at end
2003.07.01 -- added description of 1/3-comma "major-3rd" error; fixed some typos
by Joe Monzo