La meilleure voie que j'ai découverte pour saisir autant que possible d'information harmonique dans un système musical d'accord de l'intonation-juste, c'est l'utilisation des diagrammes de trellis ce qui dépeint les hauteurs comme les points dans l'espace multi-dimensionnel, relié par des vecteurs.
Dans un système d'accord d'intonation-juste, chaque note est représentée par un rapport ce qui décrit la relation de cette note à une autre note, ce qu'un est habituellement utilisé comme référence pour entier le système. Cette tonalité de référence a le rapport 1/1, également décrit en tant que 1:1 ou 1 à 1.
Tout nombre pouvoir factoriser dans le série des nombres premiers, chaque qui un base qui avoir un exposant que l'un ou l'autre positif ou négatif, ce qui représente nombre >1 ou <1, respectivement, à moins que l'exposant=0, qui représente 1, l'identité en multiplication.
Les exposants de le facteur premier 2 tout avec harmonie équivalent ce identité 1, ainsi, les exposants de 2 représenter "octave", et ainsi avoir aucun prononcé effet sur harmonie, et pouvoir éliminer, à moins que l'enregistrement de l''octave' est spécifiquement à l'étude. Par conséquent les diagrammes commencent normalement par la facteur premier 3.
Mes diagrammes de trellis traitent chaque facteur premier
comme un seul dimension dans l'espace, avec tout exposant rayonner
à l'extérieur central 1/1, ce qui est
égal à tous les facteurs avec un exposant de 0,
ou n0.
Considérer dans à deux dimensions espace,
les vecteurs qui relient chaque exposant
voyage dans une seule direction pour chacun facteur premier.
Cette direction est déterminée par l'angle
qui représente la valeur de cents (dans l''octave')
de ce facteur premier avec un exponant d'1,
à partir de la position de 6 heures.
Ainsi, 31, qui est le rapport 3/2 et est de
702 des cents, ont un vecteur rayonner dehors de 1/1 à
très de près de
la position de l'1 heure (parce que 6 + 7 mod 12 = 1).
51, qui le rapport 5/4 et de 386 des cents,
a un vecteur rayonner à l'extérieur légèrement moins de
la position de 10 heures (6 + 3.86 = 9.86), et ainsi de suite.
Les exposants négatifs rayonnent simplement
à l'extérieur de la direction opposée.
Les vecteurs changent également dans la longueur et
l'épaisseur selon les facteurs premiers qu'ils se relient, avec 3 le
plus court et le plus profondément.
C'est interessant que quoique à deux dimensions espace
milieu dans qui ces mesure faire, apparaître pour oeil pour former
3- ou même plus-dimensionnel structure, en quelque sorte ressembler
cristal.
Harry Partch
a inventé une structure qu'il a appelé
le "diamant de tonalité".
Ce montrer tout harmonique rapport avec nombre sous un certain
"impair limite"
(à l'exclusion "doubler d'octave", ou
multiplication par 2, ce qu'il a utilisé
pour conserver chaque rapport dans le
même "octave",
comme cela est le cas pour les plus habituelles les échelles).
Ces "diamant", qui simple obtenir grand et
tenir exponentiellement plus des rapports
avec chaque nouveau autre limite-d'impair
dans Partch version, prendre on un aspect
complètement différent quand
illustrer utiliser mon trellis. Le processus fait certainement appel
à mes susceptibilités artistiques.
J'illustre ici le Limite-de-5, le Limite-de-7,
le Limite-de-9, le Limite-d'-11, et le Limite-de-13
"diamants de tonalité"
comme représentés
par mes diagrammes de trellis. Symétrie qui Partch
noter dans son échelle et tonalité diamant prêt évident ici, bien
que tonalité diamant dans ce représentation non parfait
symétrique, comme quelque autre système je avoir concevoir.
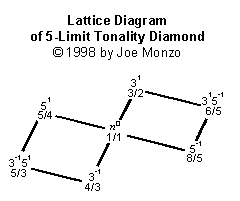
Partch appeler ce naissant tonalité diamant, parce que un triade avec proportion 4:5:6 donner l'accord maximum pour un accord avec trois identités distincts, ainsi ce simple système que pouvoir construire qui donner tout vrai sentiment tonalité.
La triade "majeur" sur mon trellis ressemble ceci
( les odentities étant donné):
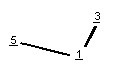
et la triade "mineur" ressemble ceci (avec des
udentities):
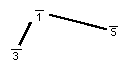
Notez que le trellis ou le diamant Limite-de-5 contient trois de chacune des triades 'majeurs' et 'mineurs' Chaque système de limite de n contient toujours (n+1) des cordes du consonance maximal, chacun avec (n+1)/2 des identités, également divisées en (n+1)/2 chacun du 'majeur' et du 'mineur'.
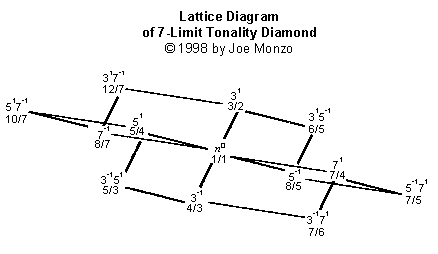
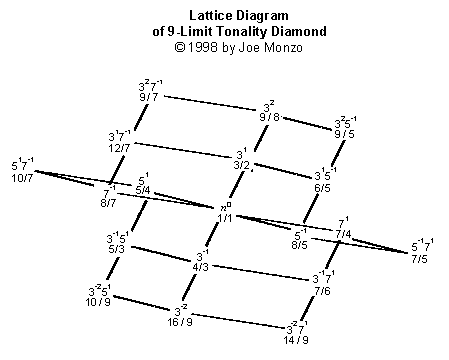
Noter que Limite-de-9 trellis n'a pas un nouveau
dimension -- seul ajouter un couche,
a l'un et l'autre fin d'un exposant de 3,
sur Limite-de-7 trellis. Ceci parce que 9 n'est pas un nombre premier,
mais plutôt un composé, c.-à-d., un
nombre composer des autres premiers,
dans ce cas-ci
3 x 3, ou 32.
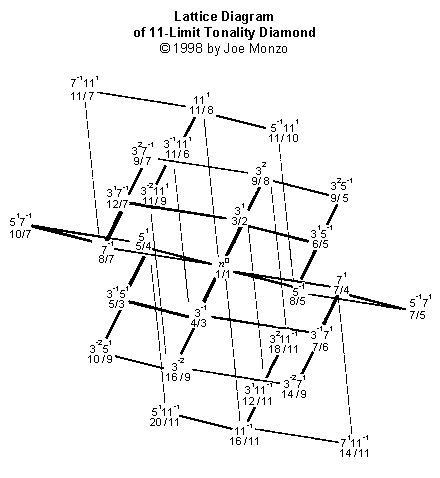
Voici une version du trellis Limite-d'-11 dans la pleine couleur:
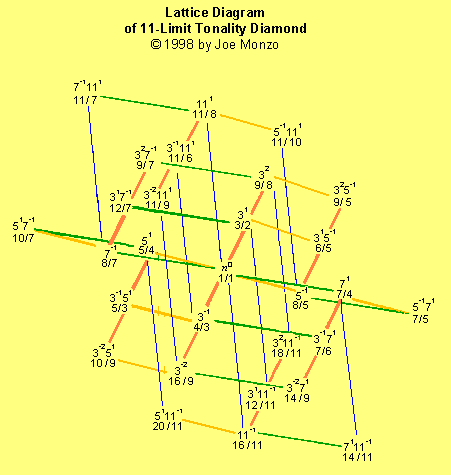
Est ensuite une version ombragée du trellis Limite-d'-11 que
j'aime surtout:
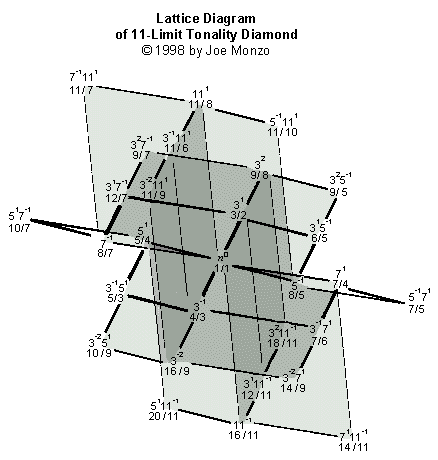
Et le plus compliqué de ceci placez, le trellis Limite-de-13:
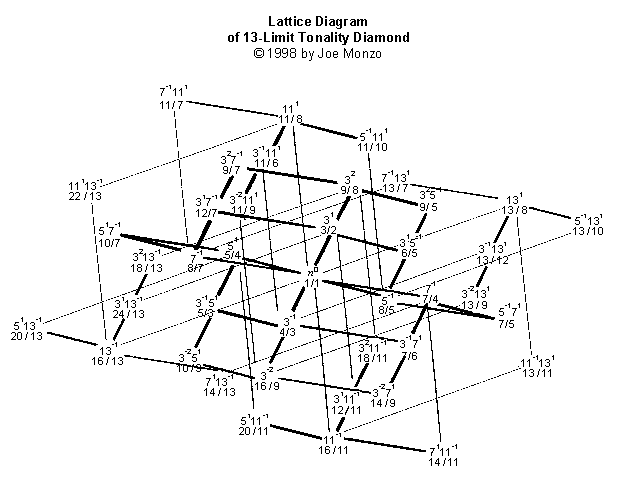
Les trellis forment complexe cristal-comme les structures qui montrent une richesse d'information harmonique d'un coup d'oeil. Si visualiser dans commande énumérer en haut, pouvoir voir que chacun petit un contenir dans grand ceux.