Die beste Möglichkeit, die ich gefunden habe, um sich in einem reinen Stimmungssystem möglichst viele harmonische Informationen vor Augen zu führen, sind Gitterdiagramme, die Tonhöhenklassen als durch Vektoren verbundene Punkte in einem mehrdimensionalen Raum darstellen.
In einem reinen Stimmungssystem wird jeder Ton durch das Verhältnis dieses Tons zu einem anderen Ton definiert, normalerweise demjenigen, der als Bezugspunkt für das ganze System dient. Dieser Bezugston hat das Verhältnis 1/1, auch 1:1 oder "1 zu 1" geschrieben.
Man kann jede Zahl in ihre Primfaktoren p zerlegen, deren Häufigkeit als Exponent pn dargestellt wird. Dabei steht n=0 für 1, das neutrale Element der Multiplikation, und n<0 für den Kehrwert der Primfaktoren, die Zahlen unter dem Bruchstrich. (vgl. prim)
Die Potenzen von 2 sind alle harmonisch der Ursprungsgröße 1 gleichwertig. Potenzen von 2 stellen also "Oktaven" dar, haben keinen ausgeprägten Effekt auf die Harmonie und können ignoriert werden, wenn kein besonderer Wert auf die "Oktav"-Lage gelegt wird. Deswegen beginnen die Diagramme normalerweise mit der Basis 3.
Meine Gitterdiagramme behandeln jede Primzahlbasis als eigene Dimension im Raum. Die Exponenten strahlen in alle Richtungen von der zentralen 1 aus, die der nullten Potenz aller Zahlen, n0, entspricht.
Im zweidimensionalen Raum betrachtet bewegen sich die Vektoren, die zu einem Primfaktor gehören, alle entlang ihrer eigenen Achse durch den Raum. Diese Achse ist durch den Winkel bestimmt, der dem ("oktav"-reduzierten) Centwert dieser Primzahl entspricht. Ausgangspunkt ist die 6-Uhr-Position.
So hat 31, das dem Verhältnis 3/2 entspricht und 702 Cent groß ist, einen Vektor, der vom Mittelpunkt 1/1 aus fast genau auf 1 Uhr zeigt, der Vektor von 51, das dem Verhältnis 5/4 entspricht und 386 Cent groß ist, zeigt auf kurz vor 10 Uhr und so weiter. Die negativen Exponenten zeigen einfach in die entgegengesetzte Richtung.
Die Vektoren schwanken auch in Länge und Stärke entsprechend den Primzahlbasis, die sie vertreten, wobei die 3 am kürzesten und dicksten ist.
Interessanterweise bilden sie für das Auge scheinbar drei- oder auch mehrdimensionale Strukturen ähnlich Kristallen, obwohl sie aus Messungen im zweidimensionalen Raum hervorgegangen sind.
Harry Partch erfand eine Struktur, die er Tonalitätsrhombus ("tonality diamond"). nannte. Dieser zeigt alle harmonischen Verwandtschaften zwischen Verhältnissen unterhalb eines bestimmten ungeradzahligen Limits (ohne "Oktav"-Verdoppelungen zu berücksichtigen, also Multiplikationen mit 2, mittels derer er alle Verhältnisse in die gleiche "Oktave" legte, wie es in den üblichsten überlieferten Skalen der Fall ist).
Diese Rhomben, die in Partchs Version mit jedem neuen ungeraden Limit größer werden und exponentiell mehr Verhältnisse beinhalten, gewinnen völlig neue Aspekte, wenn sie mit meinen Gitterdiagrammen dargestellt werden. Dieser Vorgang spricht jedenfalls mein künstlerisches Empfinden an.
Ich erkläre nun die Tonalitätsrhomben für die Limits 5, 7, 9, 11 und 13, so wie sie in meinen Gitterdiagrammen dargestellt werden.
Die Symmetrie, die Partch in seinen Skalen und Tonalitätrhomben feststellte, fällt hier sofort ins Auge, wenn auch die Tonalitätsrhomben im Gegensatz zu einigen anderen Systemen, die ich entworfen habe, nicht völlig symmetrisch sind.
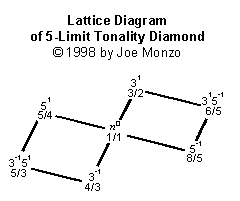
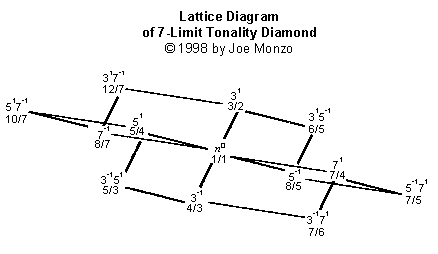
Partch nannte dies den Ursprungsrhombus der Tonalität, weil ein Dreiklang mit Frequenzen im Verhältnis 4:5:6 die höchstmögliche Konsonanz für einen Akkord aus drei verschiedenen Tönen, Identitäten, ergibt. Somit ist es das einfachste System, das sich konstruieren lässt, welches ein echtes Gefühl von Tonalität vermittelt.
Der "Dur"-Dreiklang sieht in meinem Gitterdiagramm folgendermaßen aus
(wobei die Beziehungen zwischen den Obertönen, von Partch
"Odentitäten"
genannt, angegeben sind):
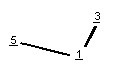
und der "Moll"-Dreiklang (mit den "Untertönen",
Udentitäten)
so:
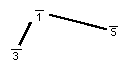
Man beachte, dass das Gitter/der Rhombus für Limit 5 je drei "Dur"- und drei "Moll"-Dreiklänge enthält. Jedes System mit dem Limit n enthält immer (n+1) Akkorde von maximaler Konsonanz, jeder davon mit (n+1)/2 Identitäten, gleichmäßig unterteilt in je (n+1)/2 mal "Dur" und "Moll.
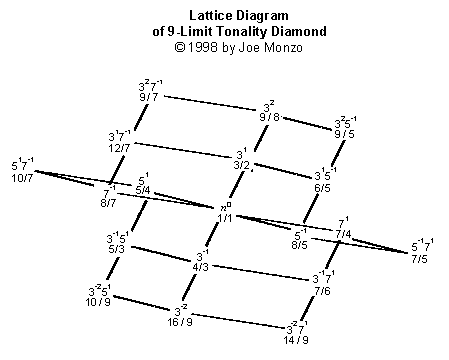
Das Gitter mit dem Limit 9 hat keine neue Dimension --
das Limit-7-Gitter bekommt lediglich eine neue Schicht
an der Achse der Basis 3. Das liegt daran, dass 9 keine
Primzahl ist, sondern aus anderen Primzahlen zusammengesetzt
ist, in diesem Fall 3 x 3 oder 32.
(Dieses
sieht auf Ihrem System möglicherweise besser aus,
das Herunterladen dauert etwas.)
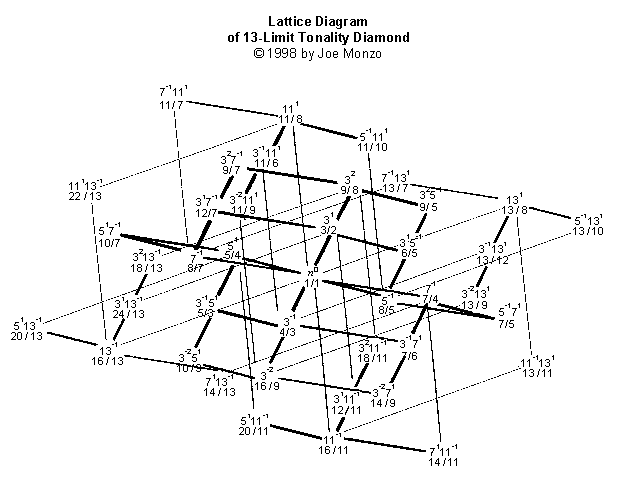
Am kompliziertesten ist dieses Gebilde, in Gitter mit dem Limit 13:
Die Gitter bilden feine kristallartige Strukturen, die auf einen
Blick eine große Menge an harmonischer Information erkennen lassen.
Betrachtet man sie in der obigen Reihenfolge, sieht man, dass jedes
kleinere Gitterdiagramm in den größeren enthalten ist.
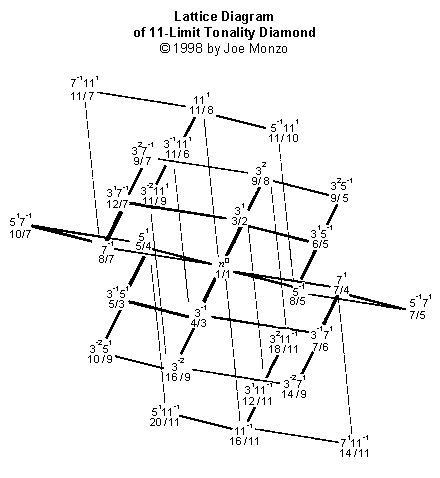
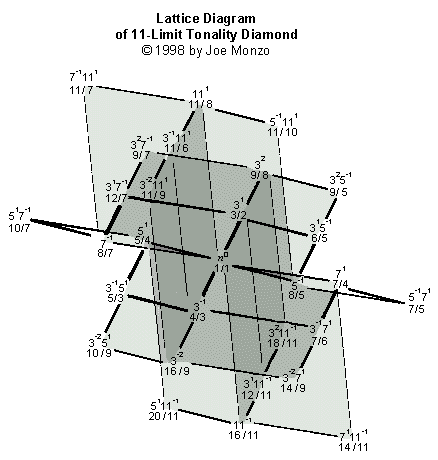
Hier ist eine farbige Version des Gitters mit dem Limit 11:
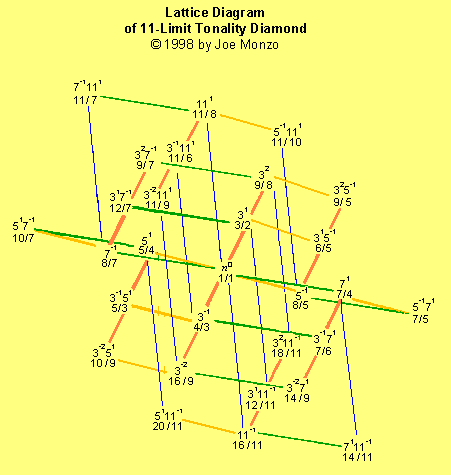
Die nächste Version des Elfergitters ist schattiert und gefällt mir am besten: