(SEE ALSO: dodekamu)
"Cawapu" is a term I coined as an acronym of
"CakewalkTM
Pitch-bend Unit", to designate the
tiny interval
available in CakewalkTM 2.0
and many other software sequencers, as
the smallest increment available for the pitch-bend controller.
It has since been superceded by dodekamu, which see for more information. However, until i redo the graphics on this page, i will keep this online as well as a supplement to the dodekamu definition.
The cawapu/dodekamu is based on the binary code used
in MIDI commands. The cawapu/dodekamu tuning spec
ignores the first two bits available in the MIDI
tuning spec's best resolution, as follows:
let "x" designate the two bits [the 8th and
the 16th] that cannot be used because they
are reserved for the SysEx flag.
let "y" designate the two bits [the 14th and 15th]
that Cakewalk's tuning spec cannot recognize.
the cawapu spec uses a total of 1+4+3+4 = 12 bits.
thus, the maximim possible value is:
xyy1 1111 x111 1111 [binary]
= 1 F 7 F [hex]
= 4095 [decimal]
note that the first nibble is essentially only
binary [i.e., a bit], as it can only be 0 or 1.
Therefore the cawapu/dodekamu gives a range of possible values from 0 to 4095 [decimal] = 00 00 to 1F 7F [hex].
For practical use in tuning MIDI-files, an interval's
semitone value
must first be calculated. The nearest
integer
semitone is translated into a MIDI note-number
(which can generally also be described by letter-name
plus optional accidental: A, Bb, C#, etc., followed
by an "octave"
register-number). Then the remainder or deficit
is converted into cawapus plus or minus, respectively.
These give the correct tuning to a tolerance that is
far better than anything that the human auditory
system can detect, or indeed far better than what
is available in the output of any electronic instruments.
cawapu-sizes for some small intervals, with
cents-values given for comparison:
interval ----------- cawapus ---------- cents
integer decimal fraction
Pythagorean comma 961 ~960.9220254 ~960 13/14 ~23.46001038
53edo comma 927 ~927.3962264 ~927 2/5 ~22.64150943
syntonic comma 881 ~880.8976219 ~880 8/9 ~21.5062896
72edo morion 683 ~682.6666667 682 2/3 16 2/3
kleisma 332 ~332.0741422 ~332 1/13 ~8.107278862
heptameride 163 ~163.2956811 ~163 2/7 ~3.986710963
savart 164 163.84 ~163 5/6 4
grad 80 ~80.07683545 ~80 1/13 ~1.955000865
skhisma 80 ~80.02440347 ~80 1/41 ~1.953720788
milli8ve 49 49.152 ~49 1/7 1.2
Türk cent 46 ~46.36981132 ~46 3/8 ~1.132075472
cent 41 40.96 40 24/25 1
monzisma 12 ~11.9765283 ~11 83/85 ~0.039863137
1/8-skhisma 10 10.00305043 ~10 1/328 ~0.244215098
jot 2 ~1.632794074 ~1 5/8 ~0.039863137
midipu 0 0.25 1/4 ~0.006103516
Note the accuracy of 10 cawapus approximating 1/8-skhisma. This makes it very easy to work with 1/8-skhisma temperaments (like Groven's and Helmholtz's) in Cakewalk.
Because 12edo
is nearly identical to
1/11-comma
meantone, if you do
much manual pitch-bend entry in Cakewalk
to retune music from 12edo into
5-limit
JI, you'll
find yourself using the following numbers again and again:
x/11-comma cawapus
1 80
2 160
3 240
4 320
5 400
6 480
7 561
8 641
9 721
10 801
11 881
12 961
13 1041
14 1121
15 1201
16 1281
17 1361
18 1441
19 1522
20 1602
21 1682
22 1762
23 1842
24 1922
25 2002
Below is a 5-limit lattice-diagram showing the amount of cawapus adjustment necessary to retune from 12edo into JI. Note periodicity (shown by different colors), in which the amount of adjustment for the interval-vector [7 1] is zero.
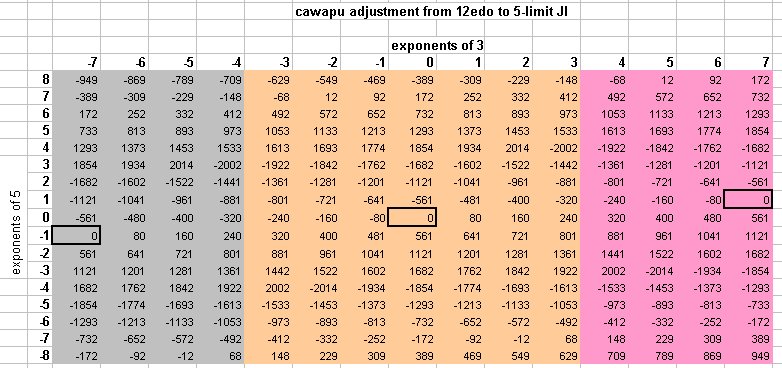
See also:
midipu
my Gentle
Introduction to the MIDI Tuning Specification
the Official
MIDI Tuning Specification.
[from Joe Monzo, JustMusic: A New Harmony]
CakewalkTM is a registered
trademark of
Twelve
Tone Systems, Inc.