Lattices
We've been publishing some nifty images of lattices on our web site without ever explaining what they are and how they help you compose great music. Well it's about time we provided some explanation. Essentially, the lattice is to harmony as most music notations are to pitch. Many music notations provide a clear visual indication of a note's relative frequency or pitch. Both staff notation and piano-roll notation are common examples of notations that readily portray the pitch of the played notes. In both cases, notes that are physically located higher on the page or screen have higher musical pitches. What most notations don't readily show are the harmonic relationships between notes in a scale or tuning.
1-Dimensional Lattice
Let's arrange the pitches of the 12-tone scale in ascending order starting with A. This is the way almost all of us think of the notes and how we're taught to think of them. This linear way of perceiving notes makes the relationship between pitch very clear. As one traverses this list from left to right, going up the scale, pitch increases.
The primary difficulty for most musicians, at least those that are not advanced composers or instrumentalists, is that the harmonic relationships between notes in the scale are not obvious from either the name or spatial relationship. One must learn and memorize that E is the perfect-5th above A and that F is the perfect-5th above Bb. We can address this problem by re-arranging the notes in the 12-tone scale according to a chain-of-5ths (related to the concept which musicians commonly know as the "circle-of-5ths"). Now our new musical scale is no longer arranged in ascending order of pitch.
If you can accept the concept of re-arranging the notes of the 12-tone musical scale according to the circle-of-5ths, you've made the logical jump to reading and understanding the lattice. A simple, one-dimensional lattice is nothing more than a number-line, where each point along the way can represent the perfect-5th for the previous point on the line. By convention, we place the tonic at the center or origin of the lattice. Additionally, we also know that the perfect-5th of the perfect-5th is a major-9th. By moving two lattice points to the right, one can readily discover the major-9th of any point on the lattice, so long as one doesn't jump off the end of the lattice.
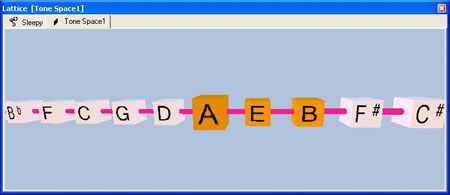
The beauty behind this lattice is that you don't even need to label the individual lattice points. Just by viewing the lattice geometry, the composer can readily see the perfect-5th and major-9th.
2-Dimensional Lattice
Unless you're satisfied composing exclusively with the tonic, the perfect-5th, and the major-9th, our lattice hasn't yet arrived. So let's take a look at both the major-3rd and the minor-3rd on the one-dimensional lattice. As you can see, the major-3rd resides four points to the right of the tonic and shown in the following major chord, while the minor-3rd is three points to the left of the tonic.
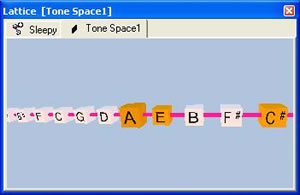
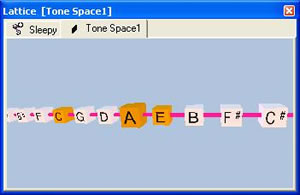
Although our 1-dimensional lattice works just fine for any interval -- if you ensure that your number-line or 1-dimensional lattice extends far enough in both directions -- this is not the great visual aid we've been talking about. As your music becomes more complex, you need to memorize an increasingly greater number of offsets from the tonic; but that's not the point of the lattice. We want to remove some of the memorization thru use of an improved visual aid.
Our solution is to add another number-line to the lattice. Let's place the second number line vertically so it doesn't interfere with the existing number line, and then let each step upward on the second number line represent the major-3rd for the lattice point below it. If you're familiar with algebra and graphing, you'll recognize our new improved lattice as simply being a two-dimensional graph. The x-axis is like our lattice's perfect-5th-axis, and the y-axis is like our lattice's major-3rd-axis.
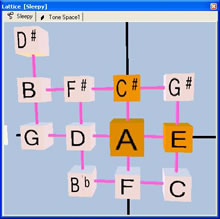
Multi-Dimensional Lattice
You might be wondering, "why go beyond two dimensions? The two-dimensional lattice is a actually a great visual aid for composing and music analysis. When you add another dimension, things will become really complicated." My answer to you is, "you're right!" Higher dimensional lattices become visually more complex. There are reasons why microtonal musicians would be interested in dealing with multi-dimensional lattices, so Tonescape was developed using 3-dimensional gaming technology to deal with higher dimensionalities. Although it's difficult to experience the 3-dimensionality on this web page, you can navigate through Tonescape lattices using virtual reality technology. Hence, 3-dimensional lattices appear very natural on Tonescape and higher-dimensional lattices reasonably easy to use.
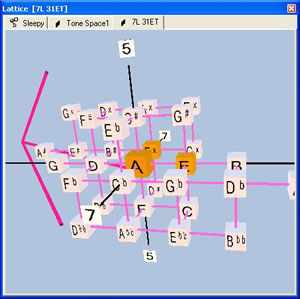
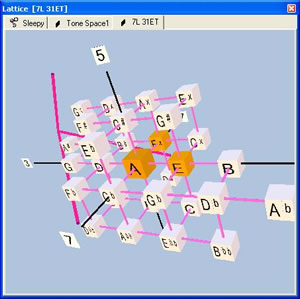
I hope you've gotten the basic feel for the lattice and just how powerful it can be as a composition and music analysis tool. As you see from this gentle introduction, lattices can come in a large number of shapes and forms based on the size of the tuning, whether or not the lattice is periodic, and the number of dimesions. What the lattice provides is a non-linear tool for thinking about musical harmony in a way that's visually appealing and visually intuitive.
