Tonescape® Tonespace Tutorial
Click here to download Tonescape®® Den Haag.
how to use "File | New | Tonespace..."
part 1: pythagorean tuning: in 1-dimensional 3-space
2005-06-03 by Joe Monzo
Contents:
2) The "File | New | Tonespace..." menu command
3) Create an Identity Vector
4) Select Prime Numbers for Axes
5) The Tonespace working environment
6) The Tonespace Editor (Tools window)
2. Tools window - Geometry tab - middle area
3. Tools window - Geometry tab - bottom area
4. Lattice views and notations
5. Changing the Cardinality
8) Compose a new Musical Piece
9) Creating an example 12-et from a Tonespace
1) Overview of creating a Tonespace (.space file)
The "File | New | Tonespace" command opens a wizard which guides you thru the creation of a Tonespace. A Tonespace is a file which sets up a prime-space (i.e., just intonation, in which the prime numbers are the axes which form the dimensions of the Tonespace), then uses Fokker unison-vector and periodicity-block theory to create a finite Tuning which tiles the Tonespace.
Tonespaces are a great way to understand how tempering works, by creating a just intonation tuning Lattice as a background -- a sort of rational numerical universe within which the Tuning is embedded, using prime-factors as the Generators of the tuning -- and then finding periodicity-blocks of appropriate Cardinalities by selecting various unison-vectors, and then making the unison-vectors vanish by dividing them up and circulating them evenly among the Generators.
When you're finished setting up your Tonespace, you may choose to either create a just intonation Tuning from your Tonespace, or to choose a method for tempering your Tonespace pitches to create a temperament. Note that you can save .space and .tuning files of the same temperament separately -- each type of file holds some different data. Tonespace .space files are used only for understanding the theory, whereas a Tuning .tuning file my be used for the creation of a Musical Piece.
The .tuning file is necessary for creating a Musical Piece, but if you use the "File | New | Tuning..." method, Tonescape currently has no way to specify how to wrap/warp the Lattice, so you can only get "Open Rectangular", "Open Triangular" and "Flat Triangular" Geometry for the Lattice in a .tuning file. If you want to be able to view the Lattice in "Closed Curved" Geometry, it is necessary to create the .tuning file out of a Tonespace, by first creating a .space file.
3) create an Identity Vector
On the first dialog box that appears, you set your identity-vector. The identity-vector exists in most tunings around the world, and is the interval by which the pattern of intervals within the scale repeats itself, and the naming of the notes also repeats in conjunction with the intervals. The identity-vector is generally, but not always, the interval known as the "octave", with the ratio 2:1 or a close approximation thereof. All of Tonescape's tuning methods will eventually allow the user to create any desired identity-vector, but in the current version, the Tonespace method is has the identity-vector fixed to the 2:1 ratio (the "octave"). So for now, just click "Next".

The identity-vector is one generator of the Tonespace, but since it defines pitch-class equivalences, it is usually ignored in theoretical considerations, and the default Lattice View does not display it -- but the user may choose to display it if desired (we will discuss this in more detail in another webpage, for now, we'll just leave it turned off).
4) Select Prime Numbers for Axes
The next dialog which opens asks you to "Select Prime Numbers for Axes". These are the prime-factors of the just intonation lattice which define each dimension of the Tonespace of the Tunings which may be created from it. Tonescape asks you to choose the primes you want in your Tonespace; the current list contains all primes up to 499.
When this dialog opens, the first available prime is already selected by default. Since prime-factor 2 by itself is already used as our identity-vector, and since the current version of Tonescape offers no other choices, the first available prime-factor is 3, and it appears selected at the top of the list of primes on the left side of the dialog.

The current version of Tonescape can deal with up to 7 dimensions, therefore, in a Tonespace which already uses 2 as the identity-vector, the user may choose up to 6 more prime-factors, and any primes may be chosen from the given list.
We will first illustrate the process by stepping thru the creation of a simple example, using only the single prime-factor 3. This creates tunings of the type known as "pythagorean".
Simply click the "Add" button to add 3 to the list of chosen prime-factors on the right side:

Since we need no other prime-factors, click the "Finish" button to exit the Create New Tonespace wizard.
5) The Tonespace working environment
The environment which appears should show at least two windows: the Tools Window showing the Tonespace Editor, and the Lattice window:

In the Lattice view, you may click anywhere on the blue background to drag the lattice to the desired location.
6) The Tonespace Editor (Tools window)
The Tools window must be open in order to see the Tonespace Editor. If the Tools window is not open, either go to the "View" menu and select "Tools"

or click on the "Tools" button on the main toolbar:

If the Tools window appears too small, it may be resized by hovering the mouse cursor over the boundary between it and the other windows until the cursor appears as a black double-headed arrow -- then click on the boundary and drag it to the desired location.
a) the "Geometry" tab
In the Tuning Editor section of the Tools window, select the "Geometry" tab.

There are three sections to the Geometry tab:
- The top area, which contains a "Cardinality" list, a "Basis" check-box, and a "Length" list, each described in detail below; /li>
- The middle area of the Tools window "Geometry" tab lists the unison-vectors which will create an equal-temperament of the selected cardinality.
- The bottom area of the Tools window "Geometry" tab is where you put the unison-vectors you've selected. Note that the bottom area does not appear in the illustration above ... the next section of the tutorial (in the box) concerns this.
Currently, it is possible that, depending on your screen resolution and the size of your windows, you may not be able to see the bottom area of the "Geometry" tab. Below is a description of how to work around this, until we can fix it:
|
There is a small problem with this: if your screen resolution is too large, you may not be able to make the Tools window big enough to show the bottom area of the "Geometry" tab. To fix this problem, you'll have to make your screen resolution smaller. Be aware that a change made to your screen resolution affects the way every program on your computer looks! Sorry that Tonescape might force you to deal with this ... we're working on it. How to change screen resolution:
|
If the bottom area of the "Geometry" tab does not appear, and your screen resolution allows you to make the Tonescape main window bigger, resize it now by dragging the bottom edge of the main window down. The bottom area of the "Geometry" tab should appear:

Now, simply hover the mouse cursor over the top edge of this "bottom area" and drag it upward a bit. The complete "Geometry" tab should look like this:

Next follows a detailed description of the operation of the "Geometry" tab.
1. Tools window - Geometry tab - top section
The top area of the "Geometry" tab contains a "Cardinality" list, a "Basis" check-box, and a "Length" list.

a. "Cardinality" list
"Cardinality" list: Choose the number of notes you want in your tuning. Choosing a number of unison-vectors equal to the number of prime-factors used as Lattice axes (i.e., the number of dimensions of the Lattice) will result in an EDO of the selected cardinality. We'll have more to say about Cardinality as we go along.
b. "Basis" check-box
"Basis" check-box: This is checked by default, and gives in the middle section of the "Geometry" tab, a list of the unison-vectors which form the kernel of the TM-reduced lattice basis. The number of basis unison-vectors is always equal to the number of prime-axes in the Tonespace -- since 3-space has only 1 dimension, we see only one unison-vector in the list in the middle area of the Geometry tab. Here is a screen-shot of the basis unison-vector which creates the default Cardinality of 31-edo in 3-space:

For a pythagorean type of tuning, 31 is actually not a good choice of Cardinality. But we will use it anyway for now, in order to illustrate a point.
c. "Length" list
The "Length" list simply extends the open ends of the tuning in the cases where a number of unison-vectors selected is smaller than the number of dimensions in the Lattice. It has no effect on a 1-dimensional tonespace, so discussed of it is deferred until later, where we create a 3,5-space.
2. Tools window - Geometry tab - middle area
The middle area of the Tools window "Geometry" tab lists the unison-vectors which will create an equal-temperament of the selected cardinality. In Tonespace of 2 or more dimensions, this area is affected by whether or not the "Basis" box is checked. But the "Basis" check-box has no effect on a 1-dimensional tonespace, so discussion of it is deferred until later, where we create a 3,5-space.
3. Tools window - Geometry tab - bottom area
The bottom area of the Tools window "Geometry" tab is where you put the selected unison-vectors.
The bottom area appears as spreadsheet-type cells, with rows of 4 asterisks (****) in the first two cells of each row, and a blank 3rd cell. The number of rows is the same as the number of prime-factor axes in the Lattice (i.e., the same as the dimensionality of the Lattice).
You simply select a unison-vector in the middle area of the "Geometry" tab by left-clicking on it, then drag it to a blank row on the bottom area. The cells in that row of the bottom area will update with the appropriate data for the selected unison-vector.
4. Lattice views and notations
Now we shall return to descriptions of different views of the Lattice window.
To select a unison-vector, left-click on the desired unison-vector in the middle area of the Geometry tab, and drag it down to a blank row of the bottom area of the Geometry tab. Doing this with our example causes the Lattice view to show a 31-tone set of adjacent pitches along the 3-axis of our lattice, displaying the default notation of ratios:

It will be instructive for us to use regular letter-name notation with sharps and flats on our Lattice. Right-click anywhere on the blue Lattice background, and choose "Select Notation" from the pop-up.

This opens the Notation Selection dialog, showing the default choice "Ratios" already selected:

Choose "Logical Meantone" and leave the Root Pitch Selector on the default choice "A" for now:

Click the "OK" button. Tonescape changes the notation on the Lattice points to the familiar letter-name notation with sharps and flats, centered on "A" as the origin.

To read the Lattice point notation better, you may zoom in on the Lattice by hovering the mouse cursor over the Lattice window (to select it) and pressing the "Page Up" key on the keyboard as many times as desired; holding down the "Page Up" key will cause a moving zoom-in effect.

In this view, our example 3-limit Lattice has the window just big enough to include all 7 of the usual nominals (A,B,C,D,E,F,G) which make up the standard diatonic scale, and also a Bb on the left of the chain-of-5ths, and an F# on the right. The interval which separates a nominal from its accompanying nominal-with-sharp or nominal-with-flat, traverses 7 steps along the 3-axis, as for example from Bb to B.
Left-click anywhere on the blue Lattice background to drag the lattice to the desired location. Let's move it to the left, so that the origin "A" is on the left side and "A#" appears on the right.

Let's change to another type of notation to see something interesting about this 7-step interval. Right-click anywhere on the blue Lattice background and choose "Select Notation" from the pop-up.

Select "Logarithmic" from the available choices. In the bottom section of the "Notation Selection" dialog, you may enter a ratio to divide logarithmically, and also a number of equal divisions. Leave it on the default values of "Magnitude = 2.000" and "Divisions = 1200", which will give us "Cents".

Click the "OK" button, and the Lattice appears as follows:

Notice that the cents value for the "A#" pitch is 114 cents. Thus, the chromatic-semitone in pythagorean tuning -- i.e., the interval which separates a letter-name nominal from the same nominal with a sharp or flat, as that between "A" and "A#" -- is about 114 cents. This is approximately the size of a 12-edo semitone, which indicates that 12-edo has some similiarities to pythagorean tuning ... we will see more about this later.
We know that the system of 12-edo can be modeled as a closed circle-of-5ths (or 4ths), which returns to its starting point. Let's see what "Select Notation | Logarithmic | Magnitude 2.0, Divisions 1200" shows us about traversing 12 steps along the 3-axis of our Lattice, i.e., in the pythagorean chain-of-5ths. Click the "OK" button, then zoom out (by pressing the "Page Down" key on the keyboard) enough so that you get 12 steps in your Lattice view.
Since a Lattice which uses only one axis creates a diagram with a long horiztonal axis, you may wish to move the Lattice window near the top of the environment, where Tonescape will tile the two windows horizontally:

You can see here that the interval of 12 5ths is only ~23 cents. This is the pythagorean-comma, with the 2,3-monzo |-19 12, >. We will return to this interval later, and use it as a unison-vector to create 12-note tunings.
Now let's try selecting a different logarithmic notation to see what it can show us. Right-click on the blue Lattice background, choose "Select Notation" from the pop-up, and "Logarithmic" from the list of choices, and leave the "Magnitude" at 2.000, but this time change the "Divisions" to 12. Since we saw that traversing 12 steps along the 3-axis results in the small pythagorean-comma, we should be able to learn something from a notation based on 12.

The Lattice now shows us that if the pythagorean tuning is notated with the nearest degree of 12-edo, then 12 steps along the 3-axis takes us back to the same note from which we started. Thus, if we temper out the pythagorean-comma, the result is 12-edo -- we shall do exactly this in just a little while.

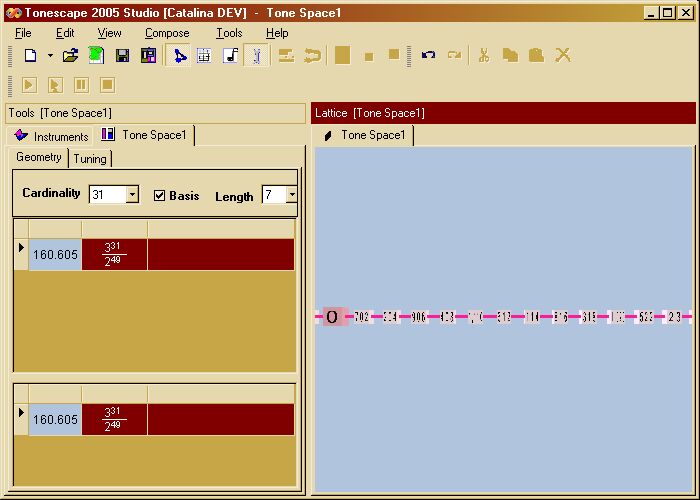
5. Changing the Cardinality
Changing the "Cardinality" changes the set of available basis unison-vectors. Let's choose a Cardinality of "7" to see how we may create the pythagorean diatonic scale. (Notice that we've gone back to the original window tiling, by clicking on the Title Bar of the Lattice window and dragging it to the desired docked location.)
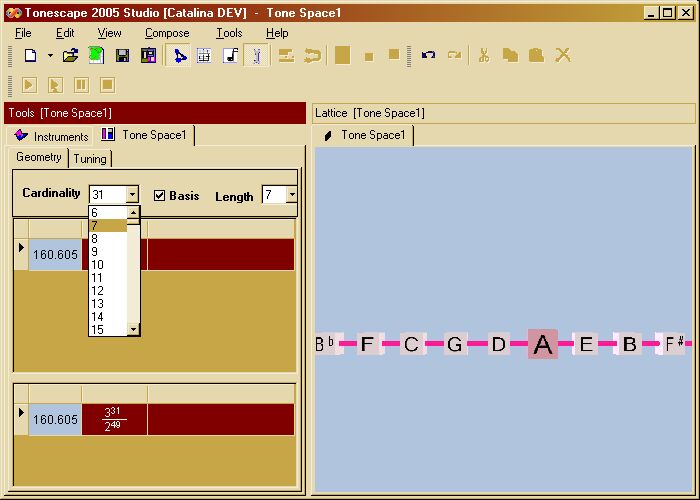
We see in this list of unison-vectors that the unison-vector which creates the diatonic scale, is the apotome, which is the pythagorean chromatic-semitone.

Left-click on the apotome in the middle area of the Geometry tab, and drag it down to the bottom area. This creates a 7-tone pythagorean diatonic scale centered on "A" on the Lattice, with a tonic of "E" for the natural minor scale.

This is a good place to stop discussion of the lattice Basis for now, so that we may progress on to the Tuning tab of the Tools window Tonespace Editor.
b) the "Tuning" tab
Left-click on the "Tuning" tab of the Tonespace Editor of the Tools window:

There are also three areas on this tab:
- The top area contains the "Temperament" check-box, which is disabled at first, and the "Cardinality" showing the number of notes which will be created in the tuning.
- The middle area contains a list of the Generators of this Tonespace, with each Generator occupying a row and the columns giving the identification of the Generator, indication of fixed or tempered values, and the actual cents or other tuning data for the Generator.
- The bottom area gives a list of pitches in the Tuning which will be created, each pitch occupying one row of the spreadsheet, and columns providing data on degree-number, prime-ratio, and verbal descriptions.
Right-click anywhere on the 3-Generator row in the middle area of the Tuning tab, and select "Create Tuning" from the pop-up:

Tonescape automatically creates a Tuning (.tuning file) out of your Tonespace. Note that this Tuning file is entirely separate from the Tonespace file, and can be edited independently. The Tuning file is what you will use to compose a Musical Piece.

We may move the windows around a bit for better viewing of the data. Here we have moved the linear 3-space Lattice to the top and zoomed in on the Lattice by pressing the "Page Up" key on the keyboard.

For purposes of our demonstration, we want to see letter-names on the Lattice points, so right-click anywhere on the blue Lattice background and choose "Select Notation" from the pop-up.

Then select "Logical Meantone" from the list of choices, and keep the "Root Pitch Selector" on the default value of "A".

Click the "OK" button. The Lattice displays letter-names on the points, in a chain-of-5ths from C to F#.

As we noted, the Tuning file may be edited separately from the Tonespace. For our demonstration, we want to use the standard pythagorean ditonic A-minor scale, the one which historically evolved first in the notation. To do this, we'll have to delete a pitch from our tuning, and add another one.
7) Edit the Tuning file
a) Tuning Editor - Generators tab
To edit a tuning file, first click on the Generators tab in the Tuning Editor window.

This shows the mathematical structure of our tuning: our example is created from two Generators, with the values of prime-factors 2 and 3. The Generators tab shows each Generator on a separate row, with the columns giving the ordinal number of the Generator, the fact that it is a Constant, its identification, its cents value, and a verbal description.
(Note that the identifier and cents value of prime-factor 3 may be edited by left-clicking on the desired cell and pressing the "F2" key on the keyboard, entering the new data, and pressing "Enter" on the keyboard. For now, we'll leave the 3-generator as it is.)
Our example is created from two Generators, one of them being prime-factor 2, and the other, prime-factor 3. Each pitch in the tuning is specified as a 2,3-monzo of exponents of these prime-factors, in the form "(a,b)" where a is the exponent of 2 and b is the exponent of 3.
b) Tuning Editor - Pitches tab
Left-click on the "Pitches" tab of the Tuning Editor to see a list of Pitches in the Tuning.

The Pitches tab puts each Pitch of the Tuning on a separate row of a spreadsheet, with the columns giving the following data (from left to right):
- scale degree in ascending order from the reference pitch
- cents value of each pitch
- monzo of each pitch
- prime-ratio of each pitch
- standard integer ratio of each pitch
- verbal description, where available
Note that the third column expresses the pitch as a 2,3-monzo of the exponents of our two generators, prime-factors 2 and 3.
We had already decided beforehand that we wanted to use the standard pythagorean A-minor scale as the tuning for our example Musical Piece -- this scale uses the 7 nominals A, B, C, D, E, F, G, with no sharps or flats. But our Tuning contains the six nominals A, B, C, D, E, G, but also has an F# instead of F. This is easy to change, simply:
-
Right-click on the F# Point on the Lattice, and select "Delete" from the pop-up.

-
The F# disappears from the Lattice:

-
Right-click anywhere on the data area of the Pitches tab spreadsheet, and select "Add Pitch" from the pop-up.

-
The Pitches tab spreadsheet updates to include a new row with a duplicate copy of whatever pitch-row was clicked, and with the monzo data selected and highlighted, ready for editing.

-
The Pitch we want to add, to replace the deleted F#, is "F", which would be one step to the left of "C" on the 3-axis of our Lattice, i.e., it has a 3-monzo of |-4, >. Since the 2-Generator is our Identity Interval, we may enter its exponent as 0 (zero) and Tonescape will calculate the appropriate exponent to normalize the Pitch into the Default Register. It is not necessary to enter the parentheses, they are supplied automatically. Thus, simply enter "0,-4" into the monzo cell.

-
While the mouse cursor is still over the monzo cell, press the "Enter" key on the keyboard, to enter the new Pitch into the Tuning. The "F" appears on our Lattice at the appropriate position to the left of "C", and our pythagorean diatonic A-minor scale is complete. Note that Tonescape automatically recalculates the ordering of the Pitches on the Pitches tab of the Tuning Editor.

(This is just a basic guide to working in the Tuning Editor, for the purpose of completing the process from creation of a Tonespace to composition of a new Musical Piece. A full treatment of working with Tonescape Tuning files is given in a separate webpage.)
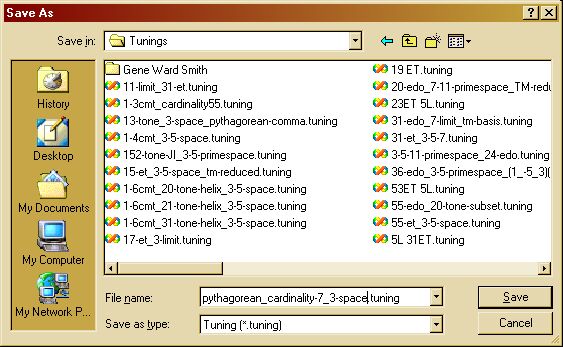
Now we may save our Tuning so that it is available for use in a Musical Piece. Right-click on the tab labeled "Tuning 1" in the Tuning Editor, and select "Save As..." from the pop-up menu.

Tonescape opens the standard Save As dialog.

Replace the "Tuning1" part of the filename with a meaningful filename, and click the "Save" button to save the .tuning file to the desired location.
Now that the .tuning file has been saved, we may composed a new Musical Piece with our pythagorean tuning.
8) Compose a new Musical Piece
Just so as to complete the process from creation of a Tonescape, thru derivation of a Tuning from that Tonespace, to composition of a new Musical Piece using that Tuning, we will here give a very brief introduction to composing a new Musical Piece with our simple 7-tone pythagorean diatonic A-minor scale. (A full treatment of composing a Musical Piece is given in a separate webpage.)
On the Menu bar at the top of the Tonescape main window, click on "File | New | Musical Piece...".

Tonescape does not assume any default tuning, so the first thing you must do is "Insert One or More Tuning Systems". (Future releases of Tonescape will allow multiple Tunings in one Musical Piece; for now, only one Tuning per Musical Piece is possible.)

Click on the "Add..." button, and Tonescape will open the Open Tuning dialog:

Select the tuning we just created, namely, "pythagorean_cardinality-7_3-space.tuning":

Click the "Open" button to add this Tuning to your Musical Piece. For now, only one Tuning per Musical Piece is possible, so click the "Finish" button.

Tonescape opens the Musical Piece window with the default Pitch Height notation selected. It is easy to see that the Pitch Height notation window is quantized to the unequal steps of our pythagorean diatonic A-minor scale.

For detailed instructions on using the Musical Piece editor, see the Tonescape Tutorial: How to compose a new Musical Piece
9) Creating an example 12-et from a Tonespace
We have just learned how to create a pythagorean diatonic scale from a 3-space Tonespace. And we saw earlier that after creating a 12-tone pythagorean chain-of-5ths, the 13th pitch brings us almost back to our starting pitch, overshooting it only by about 23 cents, the pythagorean-comma. Let's learn now how to create a tempered Tuning from our Tonespace.
Let's close the Musical Piece window (right-click on the MusicalPiece1 tab and select "Close" from the pop-up), and close our Tuning window (same procedure), click on the "Geometry" tab on the "Tonespace1" tab of the Tools window, and select "31" from the Cardinality list, to go back to our original Cardinality of 31:

Left-click on the 31-cardinality unison-vector and drag it down to the bottom area.

Now, notice that this chain-of-5ths contains both A# and Bb, C# and Db, etc. These pairs of pitches are separated by 12 steps along the 3-axis of our Lattice, which happens to be the above-noted pythagorean-comma of ~23 cents. An interval this small is a good candidate for use as a unison-vector employed in defining an equal-temperament. In fact, our very familiar standard "12-tone equal-temperament" tuning (also called "12-edo") arose historically by the very procedure we will illustrate now: the tempering-out of this same pythagorean-comma.
We already know in advance now that the Cardinality of our Tuning will be 12, so select "12" from the Cardinality list in the top area of the Geometry tab in the Tools window Tonespace1 tab.

Notice immediately that the unison-vector which Tonescape puts in the list as the basis for Cardinality 12, is the pythagorean-comma.

Select the pythagorean-comma as the unison-vector by left-clicking anywhere on its row in the middle area of the Geometry tab, and dragging it down to the blank row in the bottom area of the Geometry tab.

Note that the Lattice and the Tuning now both have only 12 pitches. Left-click on the Tuning tab of the Tools window Tonespace1 tab to select it:

If we were to right-click anywhere on the data area and select "Create Tuning" from the pop-up at this time, we would create the 12-tone pythagorean chromatic scale. However, we want to create a temperament this time, which is a bit more complicated.
a) How to create a tempered Tuning from a Tonespace
A powerful feature of Tonescape's Tonespace feature, is the ability to create tempered Tunings (temperaments) from a Tonespace, by selecting unison-vectors and distributing them among various selected ranges of pitches. The resulting tempered Tunings allow Closed Geometry views of the Lattice, which model visually some interesting mathematical properties of tunings.
Below is the detailed step-by-step procedure for creating a temperament from a Tonespace.
-
Be sure that the "Tuning" tab of the Tools window Tonespace1 tab is selected.

-
For this example, we are going to temper our Tonespace in the traditional way, leaving the 2-generator as it is so that the Identity Interval is exactly the 2/1 ratio, and tempering only the 3-generator so that the pythagorean-comma is divided up and distributed equally among all exponents along the 3-axis. Since the pythagorean-comma is nearly 24 cents and needs to be distributed among the 12 5ths in the chain, each 5th will be reduced by almost 2 cents. Left-click the mouse on the cell in the 2nd column of the 3-generator row, which is labeled "Fixed", to select it.

-
While the mouse cursor is hovering over the selected cell labeled "Fixed", press the "F2" key on the keyboard, which readies the cell for editing.

This allows you to choose either "Unison" or "Fraction" instead of fixed. We'll save detailed discussion of these for another webpage ... for now, just know that changing the value of the 3-generator to "Unison" will allow you to temper the pitches in your 3-space to create your tempered Tuning.

-
So select "Unison" from the drop-down list:

-
While you keep the mouse cursor over the "Unison" cell, press the "Enter" key on the keyboard. This enters the "Unison" value into the 3-generator cell. Notice that the verbal description in the last cell has changed.

-
Also notice that the "Temperament" check-box is now enabled. Leaving it unchecked keeps the Tonespace untempered, which we may verify on the Lattice by right-clicking on the blue background, and choosing "Select Notation | Logarithmic | Magnitude 2.000, Divisions 1200" (i.e., Cents) from the pop-up.

-
Click on the "Temperament" check-box to put the check-mark in it, and immediately the tuning of the Pitches is changed, on both the Pitches tab of the Tuning tab in the Tools window Tonespace1 tab, and on the Lattice, so that it becomes 12-tone equal-temperament (12-et). Also note that the verbal descriptions in the last column cells of the Tuning tab are changed.

-
Right-click anywhere on the data area of the Tuning tab now, to open the pop-up for "Create Tuning", and now it will create the tempered tuning.
b) Viewing the Lattice in Closed Geometry
Because 12-et tempers out the pythagorean-comma, after we traverse 12 steps in the chain-of-5ths, we end up not close to where we started as in true pythagorean tuning, but instead, exactly where we started. Thus, the Lattice may now be warped, so that the Points representing notes 13 steps apart on the 3-axis, now occupy exactly the same point in Tonespace, and therefore the chain-of-5ths now actually becomes the circle-of-5ths.
Tonescape allows a choice of Open or Closed Geometry for viewing the Lattice. In general, it is actually easier to work with the Open Geometry while using the Lattice as an aid to composing. But the Closed Geometry is useful for understanding how the mathematics of a particular temperament change the background just-intonation Tonespace.
To view the Closed Geometry, right-click anywhere on the blue background of the Lattice, select "Geometry" from the pop-up, and choose "Closed Curved" from the list of choices.

Tonespace immediately wraps the Lattice so that it now forms a 12-tone circle-of-5ths.

Hold down the "Ctrl" key while you left-click on the blue Lattice background, and then moving the mouse will rotate the Lattice in 3 dimensions. Below are some other views of the 12-tone circle:
This view rotates the Lattice so it can be seen from above, which clearly shows the circular form; notation is still in Logarithmic 1200 (Cents):

This view is the same rotation as that above, but with Logical Meantone notation. Note that the interval notated here as the diminished-6th between G# and Eb is actually exactly the same as the perfect-5ths between Ab:Eb and G#:D#, because in 12-et Ab=G# and Eb=D# etc.

This concludes our initial tutorial on how to create both pythagorean and tempered Tunings from a Tonespace. Part 2 will introduce a 2-dimensional Tonespace, with Closed Geometry which is much more complex and beautiful.



