Autumn Leaves in Blackjack scale
(This page is accompanied by an mp3 loop of the beginning of
Autumn Leaves in 12-EDO and Blackjack tuning.
download the mp3 here.)
In Yahoo Tuning Group message 22726, Mon May 14, 2001 7:53 am, Bob Valentine wrote:
> ... I wrote out a three voice > triadic harmonization of 'Autumn Leaves' > which is > > ii V I IV full cadence to vi > > and then a three voice jazz renderring > > G F# F# E E D# E > C C B B A A G > A D G C F# B E > > where seventh chords are generally > consonant. However, I don't believe > [s]eventh chords imply 7-limit in Western > music, so this line of pursuit failed...
I made an mp3 of this, first in 12-EDO (at the beginning) and then in Blackjack 21-of-72-EDO (starting at about 13 seconds).
(You should be hearing it automatically. It may also be downloaded here: beginning of Autumn Leaves in 12-EDO and Blackjack tuning.)
The Semitone values of the The regular 12-EDO tuning are as follows, with approximate frequency proportions shown below:
19 18 18 16 16 15 16
12 12 11 11 9 9 7
9 2 7 0 6 -1 4
5:6:9 4:7:10 8:10:15 8:15:20 5:6:9 4:7:10 5:6:10
The Semitone values of the Blackjack notes I chose are as follows, with approximate frequency proportions shown below:
19 18&1/6 17&5/6 15&5/6 15&1/2 14&2/3 15&5/6
12 12 10&5/6 10&1/2 8&1/2 8&1/2 7
9&1/3 2&1/3 7 0 5&5/6 -1&1/6 3&5/6
12:14:21 4:7:10 8:10:15 6:11:15 12:14:21 4:7:10 5:6:10
(Blackjack is a much closer approximation to its proportions than 12-EDO is to its proportions.)
I should have used a Blackjack scale where G = 0, but I didn't realize that until after I had done it, so C = 0.
Something pretty strange is happening between the C-major-7 and F#-minor-7 chords. I tried several different Blackjack tunings for the notes in these chords, because there was a shift at the F#-minor that didn't sound good, so I tried to smooth it out by changing some of the pitches in C-major.
I settled on the ones here by ear. The C chord has almost exactly the integer proportions 6:11:15 and is a sound I like, but the microtonal movement between these two chords sounds a little off.
I don't have an instrument that can be tuned this way and did it strictly "by eye", using these graphs:
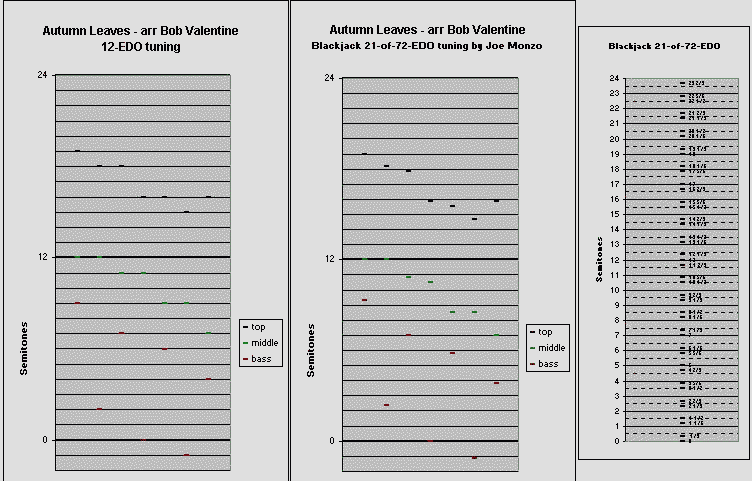
If I had a keyboard tuned to the Blackjack scale I could play around with the tune a little more and probably come up with harmonies that sound a little smoother.
But even with this defect, I still feel that the Blackjack version is much more expressive than the bland 12-EDO version, and I prefer it.
===============================================
In the correct orientation, where G=0, the Semitone values of the pitches I used above would transpose into the following:
24 23&1/6 22&5/6 20&1/2 20&1/2 19&2/3 20&5/6
17 17 15&5/6 15&1/2 13&1/2 13&1/2 12
14&1/3 7&1/3 12 5 10&5/6 4&1/6 8&5/6
Note, however, that if the Blackjack scale originated on G, it would not have all of these pitches, so some of them would have to be adjusted.
updated:
-
2001.5.14
