Eivind Groven's schismic (or schismatic) temperament
Text and diagrams © 2002 by Joseph L. Monzo
just a little over 3 years ago, Paul Erlich wrote:
> From: "Paul H. Erlich" > Date: Thu Sep 9, 1999 3:12 pm > Subject: Groven and 171-tone equal temperament? > > > I remember, years ago, reading the New Grove entry > on microtonality, to find one composer listed as using > 171-tone equal temperament. My best recollection was > that is was Groven, but after years of hearing Groven > referred to as a 36-tone JI composer, I tried to flush > that from my memory. > > So now it turns out that Groven used 1/8-schisma temperament. > Well, a 1/8-schisma tempered fifth is 701.711 cents, while > 100/171 octave is 701.754 cents. Close enough, but the > questions remain: Did New Grove actually say that? If so, > did they get it from something Groven actually said or wrote, > or did someone else note this approximation? 118-tone equal > temperament comes closer, with a fifth of 701.695 cents, > so where did 171-tET come from (if not my own confusion)? > > To tuning listers: this is of interest partially to fill > out Joe Monzo's ET table, and partially because 171 > (along with 22) just came up as the most common periodicity > block size using Fokker's unison vectors of 225:224 or > smaller. Also, 171-tET has a maximum error of 0.40 cents > in the 9-limit, making it the lowest ET to improve on 99-tET's > figure of 2.15 cents. In fact 171 is best for its size for > the 7-limit and even the 5-limit (just barely beating 118), > but not the 3-limit, where 53 is better. ...
while working on the updates to my Tuning Dictionary "Equal Temperament" page earlier today, i wanted to make sure that my information about Groven was accurate. i had him listed under 171edo as a result of Paul's post quoted above, but took Groven's name out because i haven't seen documentation that he did in fact advocate or even conceive of his tuning as having anything to do with 171edo.
so i became intrigued with Groven's tuning and decided to start digging for more info.
There's an abstract of a paper describing Groven's organ, wherein it is written:
>> "... Groven resolved to construct a keyboard capable >> of playing in pure tuning, or just intonation, >> first experimenting with the piano, and later >> succeeding with a 36-tone organ which can automatically >> adjust the tuning dynamically during performance. >> Groven's organ uses a standard keyboard manual to >> which each individual key can be connected to one >> of three possible pipes each tuned to a slightly >> different frequency."
David Code has
a
rectangular lattice showing Groven's 36-tone "pure tuning".
It is a schismic temperament in which each "5th"
is reduced by 1/8-skhisma:
>> "Using strictly pure thirds and fifths, the difference
>> between a just major third (e.g., Eb-G) and a diminished
>> fourth (e.g., D#-G) is a skhisma, or 1.628 millioctaves
>> (1.954 cents). In Groven's organ, this discrepancy is
>> distributed across the span of eight perfect fifths,
>> reducing the difference to .203 mo. (.244 cents) per fifth.
>> In otherwords, each fifth is now 584.789 mo. (701.711 cents)
>> instead of a pure 3:2 ratio with 584.964 mo. (701.955 cents).
Code's cents-values and his millioctave value for the
skhisma are accurate to 3 decimal places, but his millioctave
measurements for 1/8-skhisma, the Groven 5th, and the
Pythagorean 5th are very slightly off:
interval ~millioctaves ~cents
1/8-skhisma 0.203512582 0.244215098
skhisma 1.628100657 1.953720788
Groven 5th 584.7589881 701.7107858
3/2 ratio 584.9625007 701.9550009
Rounded to 3 decimal places, they are respectively 0.204, 584.759, and 584.963 millioctaves.
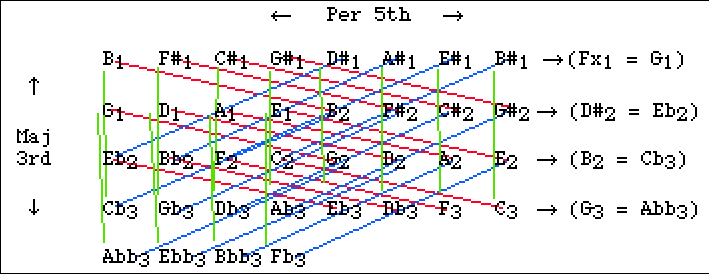
There's also a typo on Code's lattice diagram: on the right side, where it says "B2=Cb3", that should be "B3=Cb3". assuming that C2=1/1, B2 is the 15/8 ratio and already appears as such in the proper place.
Explanation of Groven's tuning
The prime-factorization of the skhisma is 2-153851, which may be expressed in vector form as [2 3 5][-15 8 1]; thus, the vector of 1/8-skhisma is [-15/8 8/8 1/8], which equates to [-15/8 1 1/8].
Groven's 1/8-skhisma-narrow "5th" may thus be notated as
a prime-factor
vector as follows:
2 3 5 interval ~cents
[ -1 1 0 ] = 3:2 ratio "perfect 5th" 701.9550009
- [-15/8 1 1/8] = 1/8-skhisma 0.244215098
------------------
[ 7/8 0 -1/8] = Groven's 1/8-skhisma "5th" 701.7107858
In addition to the subset of the 3(-3...4) * 5(-2...2) rectangular 5-limit lattice implications given by Code, Groven's tuning can be viewed as a tempered Pythagorean chain of 3(-19...+16).
The table below shows how schismatic equivalence
works in this tuning, using Groven's pair of pitches
D#2 = Eb2 as an example:
---------- prime-vector -----------
note ratio 2 3 5 2 3 5 ~cents
Eb2 32/27 5 -3 0 = 40/8 -24/8 0/8 294.1349974
* 3/8-skhisma - 45/8 -24/8 -3/8 -0.732645295
---------------------
= -5/8 0/8 3/8 294.8676427
D#2 1215/1024 -10 5 1 = -80/8 40/8 8/8 296.0887182
÷ 5/8-skhisma - -75/8 40/8 5/8 1.221075492
---------------------
= -5/8 0/8 3/8 294.8676427
Eb2 (32/27 ratio) is widened by 3/8-skhisma, while D#2 (1215/1024 ratio) is narrowed by 5/8-skhisma, so that the result is the same tempered note representing both pitches.
Note that because of the way Groven's 1/8-schismic temperament works, the "major 3rds", just as in 1/4-comma meantone, are exactly the JI 5:4 ratio.
With exact 5:4 "major 3rds", and only a 1/4-cent tempering on each "perfect 5th" giving a maximum error of only +~4.64 cents for 3-19, which falls within the common assumption that +/- 5 cents is a negligible margin of error when working in JI, Groven's tuning can indeed be considered a good and eminently practical representation of "pure tuning".
Equal-temperament approximations to Groven's tuning
It turns out that the interval separating the notes in each triplet of same-letter-name notes (or their enharmonic equivalents) in Groven's scale, which is the Pythagorean comma narrowed by 11/2 [=12/8] skhismas, is very close to one degree of 58edo [= 2(1/58)] and nearly identical to 2 degrees of 117edo [= 2(2/117)].
But since the basis for this tuning is the tempering of a Pythagorean chain, it makes more sense to find a good EDO approximation by examining the size of the "5th" and comparing to EDO equivalents.
By taking log10 of Groven's
skhismatically-narrowed "5th" and dividing by
log10 of 2 (the ratio
of the "octave"),
we find that the closest EDO approximations to the
1/8-skhisma-narrow "5th", in order of decreasing error, are:
EDO "5th" cents cents error from Groven's 5th
53 231/53 701.8867925 +1/6
171 2100/171 701.754386 +1/23
118 269/118 701.6949153 -1/63
525 2307/525 701.7142857 +1/286
as shown on this graph:
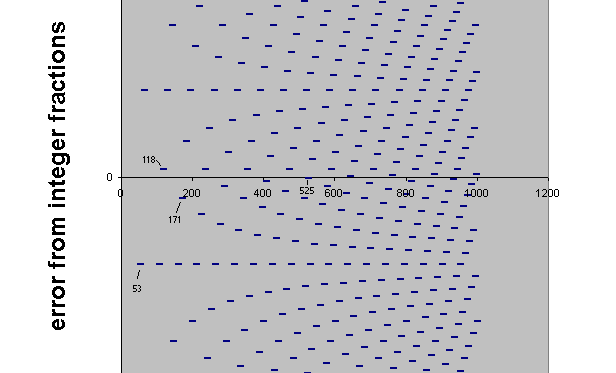
In 53edo, the interval separating each triplet as a group is 4 degrees of 53edo [= 2(4/53)] for the smaller semitones and 5 degrees of 53edo [= 2(5/53)] for the larger semitones, with 1 degree of 53edo [=2(1/53)] representing the numbers associated with Groven's pitch-labels, and thus the interval between like-named notes in each triplet. Thus, 53edo is the smallest superset EDO which contains a good approximation of Groven's tuning, and so Groven's tuning could be considered as a 36-tone subset of 53edo.
However, the 1/8-skhisma tempering of Groven's "5th" is only ~1/4-cent to begin with, and the error of 53edo from his "5th" is ~1/6-cent too large, whereas the 53edo "5th" is only ~1/12-cent narrower than the "pure" Pythagorean 3:2 "5th". So while 53edo is indeed a good approximation of Groven's skhismatic temperament, it is a still better approximation of Pythagorean tuning.
As seen above, however, 118edo provides an approximation to Groven's tuning which is a bit more accurate. The interval separating each triplet as a group is 9 degrees of 118edo [= 2(9/118)] for the smaller semitones and 11 degrees of 118edo [= 2(11/118)] for the larger semitones.
171edo does also provide a good approximation of Groven's tuning, giving 3 degrees [= 2(3/171)] between the notes of each like-named triplet, and 13 degrees [= 2(13/171)] between each smaller semitone and 16 degrees [= 2(16/171)] between each larger semitone.
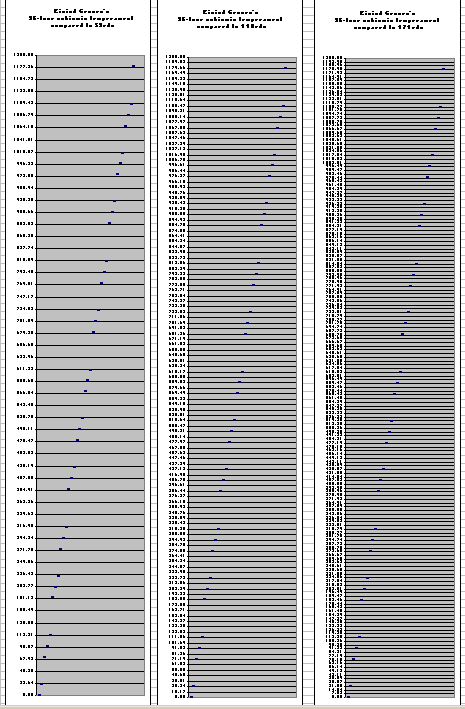
As Paul noted (in the quote at the top of this page), the 118edo and 171edo "5th" are indeed both very close to Groven's 1/8-skhisma-tempered 5th.Below are three graphs, showing Groven's scale as a subset of, respectively, 53-, 118-, and 171edo. (I know the numbers are too small to read, but this gives an overview of how his tuning fits into these EDOs.)
As to Paul's question regarding Groven's association with
171edo: i have not seen the reference in the New Grove, but
it turns out that Martin Vogel mentions Groven in
footnote 1 on p 349 of his book On The Relations Of Tone,
in connection with the automatic circuits designed by
Groven for the dynamic retuning of both his 36- and
43-tone organs, during the prelude to the exposition
on Vogel's own
171edo
electronic instrument.
Vogel never makes any connection of Groven with 171edo, but the physical proximity of the descriptions could have been enough to cause a reader to mistakenly make the association -- and oddly enough, as we saw above, it turns out that 171edo does in fact provide a superset within which a very close approximation of Groven's tuning is embedded.
Why 36 tones?
So now the question remains: since Groven was interested in expanding his pitch resources to acheive a more extensive set of notes which would provide greater concordance by emulating just-intonation, why did he choose 36 pitches as his stopping point?
First, why have a stopping point at all? If Groven was interested primarily in a method of notation for flexible-pitch instruments, such as voices or unfretted strings, he could in theory have extended the schismic chain indefinitely. But his primary intention was to provide a fixed tuning for a keyboard instrument. Since Groven assumed "octave"-equivalence, as do most tuning theorists, this necessitated a fixed number of pitches per "octave".
So the second question is: why 36 tones and not some other number?
In a private communication, Paul Erlich pretty much
echoed what i would have written here myself:
> i'm pretty sure it has to do with the mechanics of the
> instrument. once you've invested in having three
> alternates for some of the 12 keys of the keyboards,
> you might as well have three alternates for all of
> them, it makes the mechanism simpler.
>
> groven must have decided that for the purposes of the
> repertoire, two alternates would not be enough, but
> four would be too many to justify the expense.
Originally, i thought there might be a pair of unison-vectors coming into play that made 41 kind of jump out as a magic number which set the finity of Groven's conception of tuning, and that he simply lopped off a few notes on either end of the Pythagorean-chain lattice, so that it would more easily jive with the already-established 12-cardinality basis of the keyboard.
But as Paul has argued persuasively,
it makes more sense to view Groven's tuning as a complete 36-tone
torsional-block
based on a 12-tone
periodicity-block,
as there are triplets of note-names
in his nomenclature, for example:
generator --- prime-factor vector ---
2 5 2 5 ~cents ratio
12 B#3=C3 [ 28/8 -12/8] 20.5294292
0 C2 [ 0 0 ] 0 1/1
-12 Dbb1=C1=B#1 [-20/8 12/8] 1179.470571
Below is an enlarged reproduction of Code's lattice,
showing the 3
commatic
unison-vectors which are not
tempered out
in Groven's tuning: the
syntonic comma (red),
diaschisma (blue),
and diesis (green). These are the
intervals which separate notes with same letter-names
(or their
enharmonic equivalents)
but different numeric
subscripts, in each triplet of notes.
Note that Helmholtz's schismatic temperament
was a 24-note tuning which made use of two alternates
for the 12 keys of the usual
Halberstadt
keyboard. Groven's tuning is simply an expansion of this,
allowing one more alternate for each of the 12 keys.
Helmholtz's Pythagorean chain was 3(-16...+7),
and so that subset of the information given here also
describes Helmholtz's tuning. His system is also best
viewed as a 24-tone torsional-block based on a 12-tone
periodicity-block.
Tables and lattices of Groven's tuning
Below is a table showing the
prime-factor
vector,
enharmonic equivalences,
and approximate cents-values
for Groven's tuning, given as a
tempered
Pythagorean chain:
generator --- prime-factor vector ---
2 5 2 5 ~cents ratio
16 Dx3=E3=Fb3 [ 40/8 -16/8] = [ 5 -2] 427.3725723 32/25
15 Gx3=A3=Bbb3 [ 41/8 -15/8] 925.6617865
14 Cx3=D3=Ebb3 [ 34/8 -14/8] 223.9510007
13 Fx3=G3=Abb3 [ 35/8 -13/8] 722.240215
12 B#3=C3 [ 28/8 -12/8] 20.5294292
11 E#3=F3 [ 29/8 -11/8] 518.8186434
10 A#3=Bb3 [ 30/8 -10/8] 1017.107858
9 D#3=Eb3 [ 23/8 -9/8] 315.3970719
8 G#3=Ab3 [ 24/8 -8/8] = [ 3 -1] 813.6862861 8/5
/ 7 C#3=Db3 [ 17/8 -7/8] 111.9755004
| 6 F#3=Gb3 [ 18/8 -6/8] 610.2647146
| 5 B3=Cb3 [ 19/8 -5/8] 1108.553929
| 4 E2 [ 12/8 -4/8] 406.8431431
| 3 A2 [ 13/8 -3/8] 905.1323573
| 2 D2 [ 6/8 -2/8] 203.4215715
H 1 G2 [ 7/8 -1/8] 701.7107858
e 0 C2 [ 0 0 ] 0 1/1
l -1 F2 [ 1/8 1/8] 498.2892142
m -2 Bb2 [ 2/8 2/8] 996.5784285
h -3 Eb2=D#2 [ -5/8 3/8] 294.8676427
o -4 Ab2=G#2 [ -4/8 4/8] 793.1568569
l -5 Db2=C#2 [-11/8 5/8] 91.44607117
t -6 Gb2=F#2 [-10/8 6/8] 589.7352854
z -7 Cb2=B2 [ -9/8 7/8] 1088.0245
| -8 Fb1=E1 [-16/8 8/8] = [-2 1] 386.3137139 5/4
| -9 Bbb2=A1 [-15/8 9/8] 884.6029281
| -10 Ebb1=D1 [-22/8 10/8] 182.8921423
| -11 Abb1=G1=Fx1 [-21/8 11/8] 681.1813566
| -12 Dbb1=C1=B#1 [-20/8 12/8] 1179.470571
| -13 Gbb1=F1=E#1 [-27/8 13/8] 477.759785
| -14 Cbb1=Bb1=A#1 [-26/8 14/8] 976.0489993
| -15 Fbb1=Eb1=D#1 [-33/8 15/8] 274.3382135
\ -16 Bbbb1=Ab1=G#1 [-32/8 16/8] = [-4 2] 772.6274277 25/16
-17 Ebbb1=Db1=C#1 [-39/8 17/8] 70.91664196
-18 Abbb1=Gb1=F#1 [-38/8 18/8] 569.2058562
-19 Dbbb1=Cb1=B1 [-37/8 19/8] 1067.49507
(Compare this with David Code's Scale Table of Groven's Tuning.)
This table shows clearly that one of the main features of this tuning is the "pure" "major 3rds".
The "wolf 5th"
in Groven's tuning is thus:
2 3 5 ~cents
[-37/8 0 19/8] = 1067.49507 B1
- [ 40/8 0 -16/8] = 427.3725723 E3
-------------------
-77/8 0 -1/8 = 640.1224982 Groven's "wolf 5th"
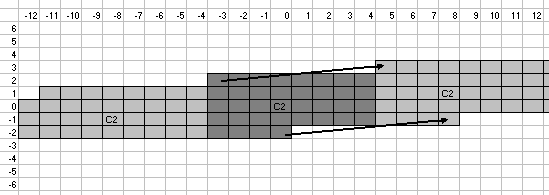
Below is a simple grid
lattice diagram
showing the 36-tone Pythagorean
chain shaded in grey.
Exponents of 3 run across the top, and exponents of 5 run
along the left side. (I know that many of the exponents are
too small to be legible ... that's OK -- the point is to show
the pattern of selected pitches amongst the whole lattice
of potential notes.)

Below is the same lattice, showing the 36-tone Pythagorean chain and also a few of its skhismatic equivalents shaded in grey. Arrows show the skhismatic equivalences.

Below is a close-up of a section of the above lattice, showing the derivation of the subset given by Code, which appears in a darker shade of grey.
updated:
2002.09.14
2002.09.20
2004.09.18 -- marked off Helmholtz subset of Groven's tuning in main table
