syntonic-comma
The musical frequency ratio 81/80, in prime-factor notation designated as 2-4345-1 or in 2,3,5-monzo form as [-4 4, -1>, expressed in decimal form as exactly 1.0125. Its logarithmic interval size is 0.22 Semitones = ~21.5062896 (~21 1/2) cents.
The syntonic-comma is the difference between the pythagorean (i.e., 3-Limit) "major 3rd" (the "ditone") of 4.08 Semitones [= 81/64 = 34 = ~407.8200035 cents] and the 5-limit "just" "major 3rd" of 3.86 Semitones [= 5/4 = 51 = ~386.3137139 cents] :
2,3,5-monzo ratio ~cents [ -6 4, 0 > = 2-6 34 81/64 407.8200035 - [ -2 0, 1 > = 2-2 51 5/4 386.3137139 --------------- [ -4 4, -1 > = 2-4 34 5-1 81/80 21.5062896
Below is a 2-dimensional Monzo lattice illustrating the [3,5] components of the prime-factorization of one example of the syntonic comma:
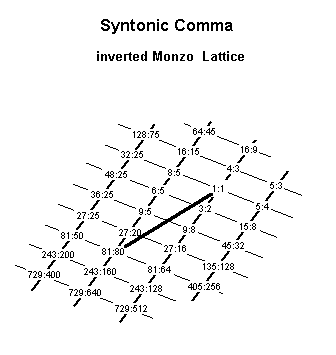
Also known as the "Comma of Didymus", who was the first theorist to specify the use of 5/4 in music theory; frequently referred to simply as "comma".
The syntonic-comma is the interval tempered out in all tunings of the meantone family. In the most direct example, 1/4-comma meantone narrows each 5th in the chain-of-5ths by 1/4 of the syntonic-comma, so that four 5ths upward, octave-reduced, equal the 5-limit major-3rd. All other varieties of meantone temper the 5th narrow by a different fraction of the syntonic-comma, so that the major-3rd is also tempered -- but the syntonic-comma still vanishes in all these tunings, so that the equation of four 5ths = major-3rd is still true.
Below are some other interval measurements for the syntonic comma:
~0.215062896 (~2/9) Semitone ~1.290377376 (~1 2/7) 72-edo-moria ~5.376572399 (~5 3/8) savarts ~11.00065477 (~11) grads ~13.08299284 (~13 1/12) 730-edo Woolhouse-units ~17.921908 (~17 59/64) millioctaves ~18.99722248 (~18 359/360) Türk-sents ~21.5062896 (~21 1/2) cents ~539.5031964 (~539 1/2) jots ~660.0392862 (~660) temperament-units ~880.8976219 (~880 8/9) 12mus ~3523.590488 (~3523 3/5) 14mus
The syntonic comma is the most important of the musical commas for the notation of musical intervals. While the pythagorean comma aids in the construction and analysis of tuning systems, the Syntonic comma defines the way thirds are notated in chords.
The syntonic comma is defined as the difference between a pythagorean major third (made from the difference twixt 4 just 3/2 perfect fifths up and 3 octaves) and a 5/4 major third:

A small interval whose ratio is 81/80 (21.5 cents [¢]).
It is the difference between the Ditone and the ratio 5/4, the Major Third of Just Intonation.
Also called the "Comma of Didymos" (latinized as Didymus).
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
