orwell
[Joe Monzo]
A name coined by Gene Ward Smith for the family of temperaments in which the semicomma vanishes (i.e., is tempered out).
The name is in honor of George Orwell, author of the book 1984, because the generator of one 11-limit version of this temperament (the 22&31 "george" variety) is 19/84-edo (AKA 19deg84).
. . . . . . . . .
[data from Gene Ward Smith, Yahoo tuning-math message 10909 (Sat Jul 17, 2004 10:03 pm)]
5 limit
| name: | orwell, semicomma |
| comma: | 2,3,5-monzo |-21 3 7> | = semicomma
| mapping: | [<1 0 3|, <0 7 -3|] |
| poptimal generator: | 43/190-edo |
| TOP period: | 1200.0 cents |
| TOP generator: | 271.599422 cents |
| MOS cardinalities: | 9, 13, 22, 31, 53, 84 |
Below are some Tonescape® lattices of 5-limit orwell temperament.
5-limit orwell, rectangular JI lattice:
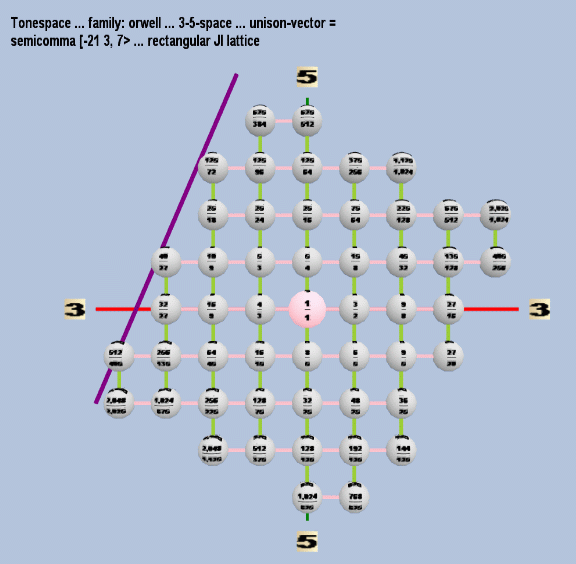
5-limit orwell, curved 7-strand helical lattice:
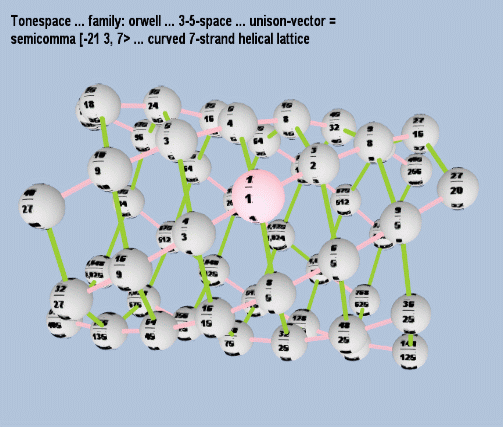
7 limit
| name: | orwell, 22&31 |
| wedgie: | <<7 -3 8 -21 -7 27|| |
| mapping: | [<1 0 3 1|, <0 7 -3 8|] |
| 7 limit poptimal generator: | 26/115-edo |
| 9 limit poptimal generator: | 43/190-edo |
| other generators: | 5/22-, 7/31-, 12/53-, 17/75-, 19/84-edo |
| TOP period: | 1199.532657 cents |
| TOP generator: | 271.493647 cents |
| TM basis: | {225/224, 1728/1715} ratios |
| MOS cardinalities: | 9, 13, 22, 31, 53, 84 |
11-limit
| name: | george, 22&31 |
| wedgie: | <<7 -3 8 2 -21 -7 -21 27 15 -22|| |
| mapping: | [<1 0 3 1 3|, <0 7 -3 8 2|] |
| poptimal generator: | 19/84-edo |
| TOP period: | 1201.251092 cents |
| TOP generator: | 271.425083 cents |
| TM basis: | {99/98, 121/120, 176/175} |
| MOS cardinalities: | 9, 13, 22, 31, 53, 84 |
| name: | orwell, 31&84 |
| wedgie: | <<7 -3 8 33 -21 -7 28 27 87 65|| |
| mapping: | [<1 0 3 1 -4|, <0 7 -3 8 33|] |
| poptimal generator: | 85/376-edo |
| TOP period: | 1200.564417 cents |
| TOP generator: | 271.443068 cents |
| TM basis: | {225/224, 441/440, 1728/1715} |
| MOS cardinalities: | 9, 13, 22, 31, 53, 84, 115, 146 |
9-note MOS:
generator note ratio
-4 Eb+ (16/15)
-3 F#- (5/4)
-2 A-< (35/24)
-1 B> (12/7)
0 D (1/1)
+1 F< (7/6)
+2 G+> (48/35)
+3 Bb+ (8/5)
+4 C#- (15/8)
Below are two graphs illustrating the example 9-note MOS given above:
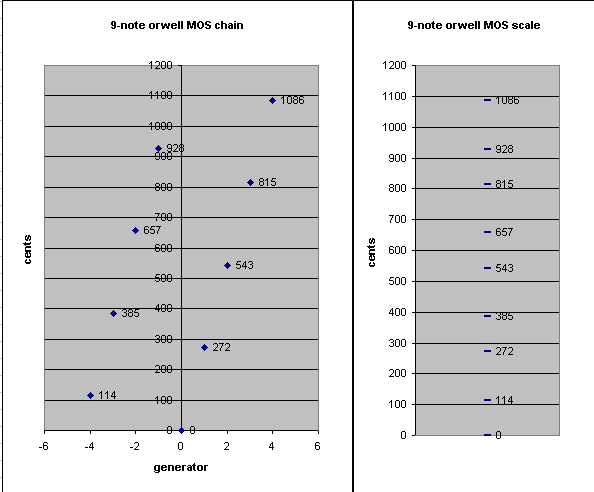
. . . . . . . . .
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
