enharmonic genus
In ancient Greek theory, one of the three basic type of genus, with a characteristic interval of approximately a "major 3rd" at the top of the tetrachord, then 2 successive intervals of approximately a quarter-tone at the bottom, making up a 4/3 "perfect 4th".
Below is a graph showing the comparative structures of tetrachords for the enharmonic genus as explained by various ancient theorists:
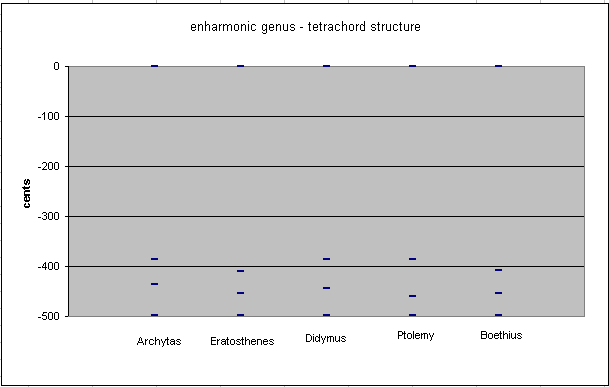
Below is a detailed examination of the enharmonic genera proposed by each writer.
Archytas
string-length proportions: 1512 : 1890 : 1944 : 2016 (reduced 84:105:108:112) note ratio ~ cents mese 1/1 0 > 4:5 ~ 386.3137139 cents lichanos 4/5 - 386.3137139 > 35:36 ~ 48.7703814 cents parhypate 7/9 - 435.0840953 > 27:28 ~ 62.96090387 cents hypate 3/4 - 498.0449991
Archytas gives the characteristic interval of his enharmonic genus as the 5-limit 5:4 "major-3rd", as described disparagingly by Aristoxenos, who preferred the Pythagorean ditone. His lichanos is thus also a 16:15 "diatonic semitone" above the bottom note hypate.
Archytas divided his enharmonic pyknon, with the string-length proportion 15:16, by multiplying these numbers by 7 (resulting in 105:112) and inserting the parhypate in between by locating it 3 units from the upper boundary of the pyknon (lichanos) and 4 units from the lower boundary (hypate), giving 105:108:112.
Eratosthenes
string-length proportions: 30 : 38 : 39 : 40 note ratio ~ cents mese 1/1 0 > 15:19 ~ 409.2443014 cents lichanos 15/19 - 409.2443014 > 38:39 ~ 44.9696465 cents parhypate 10/13 - 454.2139479 > 39:40 ~ 43.83105123 cents hypate 3/4 - 498.0449991
Eratosthenes ingeniously replaced the typical Pythagorean "ditone" for the enharmonic "characteristic interval", using instead the 19:15 "enneadecimal major-3rd" which greatly resembles the ditone; this was in order to have superparticular ratios in his pyknon, since it places lichanos a 20:19 "enneadecimal semitone" above the lowest note hypate. Then he multiplied these terms by 2 and divided his pyknon with the arithmetic mean, to give 38:39:40.
Didymus
string-length proportions: 24 : 30 : 31 : 32 note ratio ~ cents mese 1/1 0 > 4:5 ~ 386.3137139 cents lichanos 4/5 - 386.3137139 > 30:31 ~ 56.76685773 cents parhypate 24/31 - 443.0805716 > 31:32 ~ 54.96442754 cents hypate 3/4 - 498.0449991
Didymus followed Archytas in giving 5:4 as his characteristic interval, placing lichanos a 16:15 5-limit "diatonic semitone" above the lowest note hypate. Then he used Eratosthenes's method of multiplying these terms by 2 and dividing the pyknon with the arithmetic mean, to give 30:31:32.
Ptolemy
string-length proportions: 276 : 345 : 360 : 368 note ratio ~ cents mese 1/1 0 > 4:5 ~ 386.3137139 cents lichanos 4/5 - 386.3137139 > 23:24 ~ 73.6806536 cents parhypate 23/30 - 459.9943675 > 45:46 ~ 38.05063167 cents hypate 3/4 - 498.0449991
Ptolemy also retained the 5:4 5-limit "major-3rd" "characteristic interval" of Archytas and Didymus. However, he did not use the simple expedient of finding the arithmetic mean of his pyknon to locate parhypate. The fact that the proportions for the pyknon cannot be reduced further than 345:360:368 leads me to believe that Ptolemy was trying hard to give a measurement which reflected actual practice in his time.
Boethius
string-length proportions: 384 : 486 : 499 : 512 note ratio ~ cents mese 1/1 0 > 64:81 ~ 407.8200035 cents lichanos 64/81 - 407.8200035 > 486:499 ~ 45.70020208 cents parhypate 384/499 - 453.5202055 > 499:512 ~ 44.5247936 cents hypate 3/4 - 498.0449991
Boethius reverted to the Pythagorean 81:64 "ditone" for his "characteristic interval". Then he located his parhypate simply by finding the arithmetical mean between his other ratios, using the formula parhypate = lichanos + ((hypate-lichanos)/2).
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
