@ 00 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Login   |  Encyclopedia Index

torsion

When a multimonzo doesn't have a GCD of 1, that is an example of 'torsion'.

Paul Erlich's favorite definition (by Gene Ward Smith modified by Paul):

Torsion describes a condition wherein an independent set of n unison vectors fails to define a periodicity block of dimension n, because of the existence of torsion elements, meaning intervals which are not members of the group generated by the unison vectors, but some power of which are.

Gene's further revised definition:

Torsion describes a condition wherein an independent set of n unison vectors {u1, u2, ..., un} defines a non-epimorphic periodicity-block, because of the existence of a torsion element, meaning an interval which is not the product u1^e1 u2^e2 ... un^en of the set of unison vectors raised to (positive, negative or zero) integral powers, but some integer power of which is.

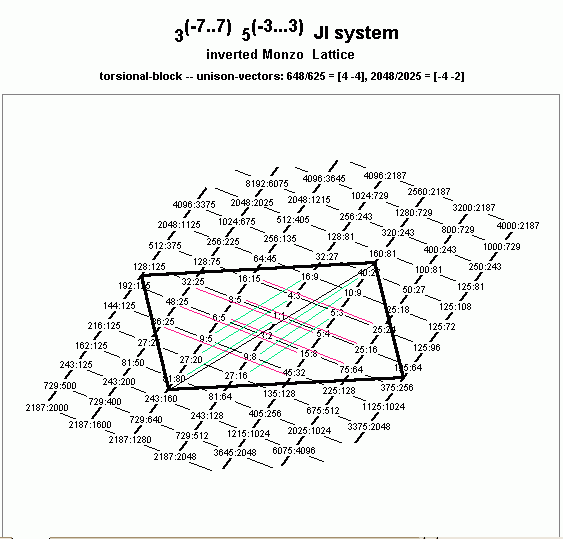
An example would be a block defined by 648/625 and 2048/2025; here 81/80 is not a product of these commas, but (81/80)² = (648/625) (2048/2025)^(-1) [from Monzo: This is illustrated on the lattice diagram below:]

• the heavy black lines are the bounding unison-vectors,
• the red lines show pairs of pitch-classes which are separated by a diesis (ratio 128:125 = [0 -3] ),
• and the green lines show pairs of pitch-classes which are separated by a syntonic comma (ratio 81:80 = [4 -1] ).
• The thin black line which divides the block in half diagonally is the torsional interval, 6561:6400 = [-8 2] = (81/80)² = (648/625) (2048/2025)^(-1).]

Torsion may be tested by forming the n by n+1 matrix whose rows correspond to the unison vectors, and calculating the GCD of the minors of the matrix. If the rows are linearly independent but the gcd is not one, we have torsion.

The term comes from mathematical usage, see Mathworld's "Torsion Group" definition.

> > > Now, the quotient module being finite...
> >
> > Whups--you are sticking "2" into the mix when you conclude this.
> > The math is more straightforward if you treat 2 as just
> > another prime number.
> >
>
> 2 is just another prime number, sure - but where exactly
> > do you think I confuse something?

Monzo's example was the block defined by 2048/2025 and 648/625; if we mod out the free group on three generators {2,3,5} by the subgroup defined by the above, we produce a mapping onto Z x Z/2Z. This has a nontrivial torsion part, so the block is a torsion block.

Using wedge products, which in the 5-limit we can identify with the cross-product, we have 2048/2025 ^ 648/625 = [11 -4 -2] ^ [3 4 -4] = [24 38 56] = 2 * [12 19 28], showing the 2-torsion. For this to work, the vectors need to be defined using the 2; Monzo unfortunately left this off and the page should be changed.

A simple method for removing torsion:

--- In tuning-math@yahoogroups.com, "monz" wrote:

> hi Gene,
>
>
> i tried deriving a periodicity-block for
> 24-ET from a <3,5,11>-prime-space by using
> the following unison-vectors:

 2,3,5,11-monzo     ratio


[ -4 4, -1, 0 >     81:80

[  7 0, -3, 0 >    128:125

[-17 2,  0, 4 > 131769:131072
		

> but instead of getting a 24-tone periodicity-block,
> i got a 48-tone torsional-block.
>
>
> 24-ET represents ratios-of-11 so well that there
> has to be a periodicity-block hiding in here somewhere.
> can you help?

i'm not sure what you're asking gene. you'd like to remove the torsion? simple -- note that the sum of the three rows in the matrix above is

which is the square of

using this for the third row of the matrix, you get

  2,3,5,7-monzo     ratio

[ -4 4, -1 0 >   81:80

[  7 0, -3 0 >  128:125

[ -7 3, -2 2 > 3267:3200

and the torsion is gone.

Torsion describes a condition where a set of pitch-classes appears to create a periodicity-block, when in reality that apparent periodicity-block is actually composed of two or more (call it n) identical smaller periodicity-blocks, each exactly 1/n as large as the apparent one, whose pitch-classes are separated by some interval which must be one which is not included within the actual smaller periodicity-block itself.

A classic example of torsion is in Monzo's attempt to analyze the traditional Indian system of tuning as an incomplete 24-tone periodicity-block, in Monzo, The Indian sruti system as a periodicity-block. There, one may see that the "torsional block" I calculated is composed of two 12-tone periodicity-blocks defining Ellis's Duodene, separated by the ditone (i.e., the pythagorean "major 3rd") with the ratio 81:64.

It may disclosed whether the condition of torsion is present, as follows:

The function igcd(n1, n2, ..., nk) in Maple™ returns the greatest common divisor of k integers. ... If you have a matrix with k-1 rows and k columns, you can produce k different square matrices by removing one of the columns; these (or the determinants of these) are called minors. ... The proceedure would be to get the k different integers det(min_j), 1 <= j <= k, where min_j is the matrix you get by removing the j th column, and take igcd(det(min₁), ..., det(min_k)). If this is not 1, then you have torsion.

So if torsion is present, the number of pitch-classes within the periodicity-block may be found by dividing the determinant by the torsion factor.

Gene's further comments:

I would suggest adding something to explain why it is called "torsion"--namely, the existence of torsion elements. If you decide to temper out 6561/6250 and 128/125, then 81/80 is not a unison, but (81/80)^2 is. It is therefore an element of finite order, which is called a torsion element.

Here is what Mathworld has to say, which you could link to: http://mathworld.wolfram.com/TorsionGroup.html.