chromatic genus
In ancient Greek theory, one of the three basic types of genus. It had a characteristic interval of approximately a minor 3rd at the top of the tetrachord, then 2 successive intervals of approximately a semitone at the bottom, making up the 4/3 perfect 4th.
Below is a graph showing the comparative structures of tetrachords for the chromatic genus as explained by various ancient theorists:
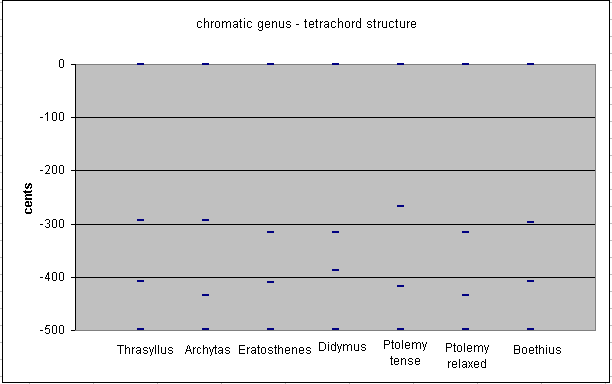
Thrasyllus
string-length proportions: 1728 : 2048 : 2187 : 2304 note ratio ~ cents mese 1/1 0 > 27:32 ~ 294.1349974 cents lichanos 27/32 - 294.1349974 > 2048:2187 ~ 113.6850061 cents parhypate 64/81 - 407.8200035 > 243:256 ~ 90.22499567 cents hypate 3/4 - 498.0449991
As with the classic Pythagorean diatonic described by Philolaus, Thrasyllus's chromatic, if extended beyond the single tetrachord, could be tuned using the method of "tuning by concords", using 3:2 perfect-5ths and 4:3 perfect-4ths up and down from the starting-note mese.
Thrasyllus's top interval is the Pythagorean 32:27 trihemitone minor-3rd, the middle interval is the Pythagorean 2187:2048 apotome "greater semitone", and the bottom interval is the Pythagorean 256:243 limma "lesser semitone". Parhypate lies a Pythagorean 81:64 ditone major-2nd below the top note mese, and lichanos lies a Pythagorean 9:8 "greater tone" above the bottom note hypate.
Archytas
string-length proportions: 1512 : 1792 : 1944 : 2016 note ratio ~ cents mese 1/1 0 > 27:32 ~ 294.1349974 cents lichanos 27/32 - 294.1349974 > 224:243 ~ 140.9490979 cents parhypate 7/9 - 435.0840953 > 27:28 ~ 62.96090387 cents hypate 3/4 - 498.0449991
Archytas measured the upper boundary of his pyknon as a limma below that of the diatonic, making his lichanos the same Pythagorean 32:27 trihemitone below the top note (mese) of the tetrachord as that described by Thrasyllus. This lichanos is also a 9:8 "tone" above the bottom note hypate; Archytas's chromatic pyknon thus has the string-length proportion 8:9; multiplied by 28 and with the middle note inserted the proportions are 224:243:252, with the respective arithmetic differences of 19 and 9.
Archytas's parhypate is the same as in his diatonic genus and enharmonic genus. (For a discussion of Archytas's idiosyncratic use of 28:27 as the lowest interval in all three of his genera, see the explanation of his diatonic genus.)
Eratosthenes
string-length proportions: 15 : 18 : 19 : 20 note ratio ~ cents mese 1/1 0 > 5:6 ~ 315.641287 cents lichanos 5/6 - 315.641287 > 18:19 ~ 93.6030144 cents parhypate 15/19 - 409.2443014 > 19:20 ~ 88.80069773 cents hypate 3/4 - 498.0449991
For his characteristic interval at the top of the tetrachord, Eratosthenes replaced the Pythagorean "trihemitone" with the 5-limit 6:5 JI minor-3rd. The lichanos is therefore also a 5-limit 10:9 "lesser tone" above the bottom note hypate. Eratosthenes then multiplied these terms by 2 and divided this pyknon by its arithmetic mean to get the superparticular proportions 18:19:20. Note that his parhypate is the "enneadecimal major-3rd" which is very similar to the Pythagorean 81:64 "ditone", making the bottom part of the tetrachord resemble that of Thrasyllus.
Didymus
string-length proportions: 60 : 72 : 75 : 80 note ratio ~ cents mese 1/1 0 > 5:6 ~ 315.641287 cents lichanos 5/6 - 315.641287 > 24:25 ~ 70.67242686 cents parhypate 4/5 - 386.3137139 > 15:16 ~ 111.7312853 cents hypate 3/4 - 498.0449991
Didymus retained the 5-limit 6:5 minor-3rd "characteristic interval" introduced by Eratosthenes, then altered the other two ratios so that his entire chromatic genus is 5-limit, introducing the 25:24 "chromatic semitone" in the middle and (as he had done in his diatonic genus) the 16:15 "diatonic semitone" at the bottom of the tetrachord.
Ptolemy - tense (syntonon, frequently translated poorly as "intense")
string-length proportions: 66 : 77 : 84 : 88 note ratio ~ cents mese 1/1 0 > 6:7 ~ 266.8709056 cents lichanos 6/7 - 266.8709056 > 11:12 ~ 150.6370585 cents parhypate 11/14 - 417.5079641 > 21:22 ~ 80.53703503 cents hypate 3/4 - 498.0449991
In his "tense" version of the chromatic genus, Ptolemy used the narrow 7:6 "septimal minor-3rd" as his "characteristic interval" at the top of the tetrachord, thus simultaneously placing his lichanos a wide 8:7 "septimal tone" above the bottom note hypate. The middle interval is the 12:11 "undecimal neutral 2nd", functioning here as a very wide semitone.
Ptolemy - relaxed (malakon, frequently translated poorly as "soft")
string-length proportions: 105 : 126 : 135 : 140 note ratio ~ cents mese 1/1 0 > 5:6 ~ 315.641287 cents lichanos 5/6 - 315.641287 > 14:15 ~ 119.4428083 cents parhypate 7/9 - 435.0840953 > 27:28 ~ 62.96090387 cents hypate 3/4 - 498.0449991
For his "relaxed" version of the chromatic genus, Ptolemy chose for his "characteristic interval" the same 5-limit 6:5 "minor-3rd" as Eratosthenes and Didymus. Note Ptolemy's placement of parhypate a wide 9:7 "septimal major-3rd" below the top note mese, as in Archytas's version of the chromatic genus, and thus giving the same 28:27 as Archytas for his lowest interval. The middle interval is therefore the 15:14 "septimal semitone".
Boethius
string-length proportions: 192 : 228 : 243 : 256 note ratio ~ cents mese 1/1 0 > 16:19 ~ 297.5130161 cents lichanos 16/19 - 297.5130161 > 76:81 ~ 110.3069873 cents parhypate 64/81 - 407.8200035 > 243:256 ~ 90.22499567 cents hypate 3/4 - 498.0449991
Boethius's parhypate is an 81:64 Pythagorean "ditone" below the top note mese, and therefore a Pythagorean 256:243 limma "lesser semitone" above the lowest note hypate.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
