Andreas Werckmeister proposed a number of temperaments which fall into the category now known as "well-temperaments", also called "circulating" or "irregular" temperaments.
In contrast to the various meantone tunings, which are based on tempering by fractions of the syntonic comma, Werckmeister's well-temperaments are all based on tempering by fractions of the pythagorean comma.
These tunings are closed 12-tone systems, intended primarily for use on keyboards; thus, all pitches mapped to the black-keys can be taken as either sharps or flats.
The first two tunings which were described by Werckmeister were not considered "good": just-intonation ("Werckmeister I"), which he considered "too perfect", and an extended form of 1/4-comma meantone with more than 12 notes ("Werckmeister II"), where the keyboard had split keys, and which he considered "incorrect". He is known today primarily for his "III" temperament, which is analyzed here in detail. (More information will follow in the future about his other temperaments.)
In octave-equivalent terms, here's how Werckmeister III works:
The 4 "5ths" between C:G:D:A and B:F# are tuned 1/4 of a pythagorean comma narrow, and all the rest of the "5ths" are tuned to the Pythagorean 3:2 ratio.
Werckmeister III narrow "5th" = (3/2) / ( ((2^-19)*(3^12))^(1/4) ) in monzo notation: 2^x * 3^y ~cents [-1 1] 3:2 ratio = "perfect 5th" 701.9550009 - [-19/4 3] 1/4 Pythagorean-comma - 5.865002596 --------------- --------------- [ 15/4 -2] Werckmeister #1 narrow 5th 696.0899983
Below is a table showing Werckmeister III tuning as a chain of "5ths".
--"5th" size--
note comma --vector-- cents comma cents
mistuning 2 3 mistuning
G# -1 [11 -4] 792.180
> 0 701.955
C# -1 [12 -5] 90.225
> 0 701.955
F# -1 [13 -6] 588.270
> -1/4 696.090
B -3/4 [ 9&1/4 -4] 1092.180
> 0 701.955
E -3/4 [10&1/4 -5] 390.225
> 0 701.955
A -3/4 [11&1/4 -6] 888.270
> -1/4 696.090
D -1/2 [ 7&1/2 -4] 192.180
> -1/4 696.090
G -1/4 [ 3&3/4 -2] 696.090
> -1/4 696.090
C 0 [ 0 0] 0.000
> 0 701.955
F 0 [ 1 -1] 498.045
> 0 701.955
Bb 0 [ 2 -2] 996.090
> 0 701.955
Eb 0 [ 3 -3] 294.135
> 0 701.955
G# -1 [ 4 -4] 792.180
(Note: in this table, fractional exponents of 2 must be given for the Werckmeister 5ths, but since the scale was normally tuned first in one reference octave and then other 8ves tuned from that, any of the exponents of 2 can be adjusted +/- any integer value without affecting the properties inherent in the tuning; thus, the G# [11 -4] tuned a narrow 5th above C# is essentially the same as the G# [4 -4] tuned a 3:2 below Eb -- the exponent of 3 is -4 in both cases, and the 7-octave difference of 2(11-4) = 27 is irrelevant.)
The Werckmeister 5ths are those between C:G:D:A and B:F#/Gb. The 5ths between Gb/F#:Db/C#:Ab/G#:Eb/D#:Bb/A#:F:C and A:E:B are 3:2 ratios.
612-edo gives a superb approximation of Werckmeister III, the maximum deviation being only ~1/29-cent. Below is a graph of Werckmeister III tuning as a scale within one octave, given as 612-edo degrees. The major divisions on the y-axis quantize it into the 612-edo representations of 12-edo for comparison. Note that 612-edo divides exactly into 12, so it provides an excellent means of comparison between 12-edo and Werckmeister III without the need for decimal or fractional parts.
~12edo ~612edo skhismas
note degrees correction ~cents error of 612edo from Werckmeister
B 11 -4 -1/43
Bb 10 -2 -1/86
A 9 -6 -1/29
Ab/G# 8 -4 -1/43
G 7 -2 -1/86
F# 6 -6 -1/29
F 5 -1 -1/173
E 4 -5 -1/35
Eb 3 -3 -1/58
D 2 -4 -1/43
C# 1 -5 -1/35
C 0 0 0
200-edo also gives an excellent approximation of Werckmeister III, the maximum deviation being only ~1/4-cent. Below is a graph of Werckmeister III tuning as a scale within one octave, given as 200-edo degrees. The major divisions on the y-axis quantize it into the 200-edo representations of 12-edo for comparison; note that 200-edo does not divide evenly into 12.
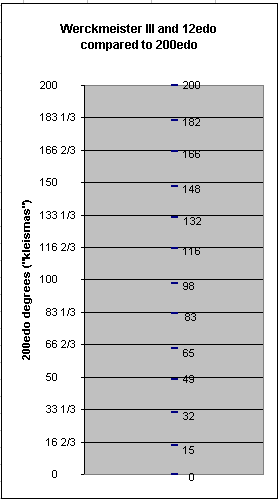
~12edo ~200edo kleismas degrees correction ~cents error B 11 -1+(1/3) -1/6 Bb 10 -2/3 -1/11 A 9 -2 -1/4 G# 8 -1+(1/3) -1/6 G 7 -2/3 -1/11 F# 6 -2 -1/4 F 5 -2/7 -1/22 E 4 -1+(3/5) -1/4 Eb 3 -1 -1/7 D 2 -1+(1/3) -1/6 C# 1 -1+(3/5) -1/4 C 0 0 0
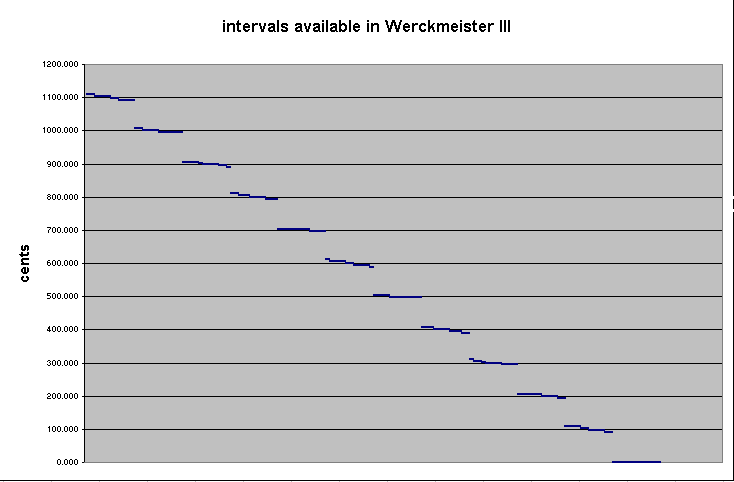
Below is a list of all intervals available in Werckmeister III:
~cents ~612edo instances
skhismas
diminished 8ve / major 7th
1109.775 566 F#:F, C#:C
1103.910 563 B:Bb, A:G#, E:Eb, G#:G
1098.045 560 D:C#, Eb:D
1092.180 557 G:F#, F:E, Bb:A, C:B
minor 7th / augmented 6th
1007.820 514 D:C, A:G
1001.955 511 G:F, F#:E, E:D, C#:B
996.090 508 B:A, Eb:C#, Bb:G#, F:Eb, G#:F#, C:Bb
diminished 7th / major 6th
905.865 462 Eb:C, F#:Eb, G#:F, C#:Bb
900.000 459 B:G#, E:C#, A:F#, Bb:G, D:B
894.135 456 G:E, F:D
888.270 453 C:A
minor 6th / augmented 5th
809.775 413 A:F, E:C
803.910 410 B:G, D:Bb, F#:D
798.045 407 G:Eb, G#:E, C#:A, Eb:B
792.180 404 F:C#, Bb:F#, C:G#
"perfect" 5th
701.955 358 F#:C#, A:E, F:C, Bb:F, G#:Eb, C#:G#, Eb:Bb, E:B
696.090 355 B:F#, D:A, C:G, G:D
diminished 5th / augmented 4th ("tritone")
611.730 312 F#:C
605.865 309 B:F, A:Eb, E:Bb, C#:G
600.000 306 D:G#, G#:D
594.135 303 G:C#, Bb:E, Eb:A, F:B
588.270 300 C:F#
"perfect" 4th
503.910 257 D:G, G:C, A:D, F#:B
498.045 254 B:E, G#:C#, Bb:Eb, Eb:G#, C:F, F:Bb, C#:F#, E:A
diminished 4th / major 3rd
407.820 208 G#:C, F#:Bb, C#:F
401.955 205 B:Eb, A:C#, E:G#, Eb:G
396.090 202 D:F#, Bb:D, G:B
390.225 199 C:E, F:A
minor 3rd / augmented 2nd
311.730 159 A:C
305.865 156 D:F, E:G
300.000 153 B:D, C#:E, F#:A, G:Bb, G#:B
294.135 150 Bb:C#, F:G#, C:Eb, Eb:F#
major 2nd / diminished 3rd
203.910 104 Bb:C, F#:G#, Eb:F, C#:Eb, G#:Bb, A:B
198.045 101 B:C#, D:E, E:F#, F:G
192.180 98 G:A, C:D
minor 2nd / augmented prime
107.820 55 B:C, A:Bb, E:F, F#:G
101.955 52 D:Eb, C#:D
96.090 49 G:G#, Eb:E, G#:A, Bb:B
90.225 46 C:C#, F:F#
unison
0.000 0 C:C, C#:C#, D:D, Eb:Eb, E:E, F:F, F#:F#, G:G, G#:G#, A:A, Bb:Bb, B:B
ANALYSIS OF WERCKMEISTER III TRIADS cents values given for the major and minor 3rds MAJOR ----- with Pythagorean 3:2 ratio "perfect 5th", ~701.955 cents: Ab, F#/Gb, and C#/Db-major are entirely Pythagorean: ~cents ~612edo skhismas Eb C# G# 294.135 150 C Bb F 407.820 208 G# F# C# A, E, and Eb-major are quite similar to <12-eq>12edo, with the major-3rd and perfect-5th ~2 cents wider: E B Bb 300.000 153 C# G# G 401.955 205 A E Eb Bb-major has a major-3rd ~4 cents smaller than 12edo and a minor-3rd intermediate between 12edo andmeantone: F 305.865 156 D 396.090 202 Bb F-major has a major-3rd ~4 cents wider than JI/meantone, and a minor-3rd ~1.5 cents wider than meantone: C 311.730 159 A 390.225 199 F with tempered "5th" 1/4-comma narrow, ~696.090 cents: B-major has the pseudo-12edo major-3rd on the bottom and the Pythagorean minor 3rd on top: F# 294.135 150 Eb 401.955 205 B D and G-major have a major-3rd ~4 cents smaller than 12edo and a minor 3rd which is exactly the same as 12edo: A D 300.000 153 F# B 396.090 202 D G C-major has a major-3rd a few cents wider than JI/meantone and a minor-3rd intermediate between and 12edo and meantone: G 305.865 156 E 390.225 199 C MINOR ----- with Pythagorean 3:2 ratio "perfect 5th", ~701.955 cents: F, Eb, and Bb-minor are entirely Pythagorean: ~cents ~612edo skhismas C Bb F 407.820 208 G# F# C# 294.135 150 F Eb Bb G#/Ab, F#, and C#-minor are very similar to 12edo, with the major-3rd and perfect-5th ~2 cents wider: Eb C# G# 401.955 205 B A E 300.000 153 G# F# C# E-minor has a minor-3rd intermediate between 12edo and meantone and a major-3rd ~4 cents smaller than 12edo: B 396.090 202 G 305.865 156 E A-minor has a minor-3rd ~1.5 cents wider than meantone, and a major-3rd ~4 cents wider than JI/meantone: E 390.225 199 C 311.730 159 A with tempered "5th" 1/4-comma narrow, ~696.090 cents: C-minor has the Pythagorean minor 3rd on the bottom and the pseudo-12edo major-3rd on top: G 401.955 205 Eb 294.135 150 C B-minor and G-minor have a minor 3rd which is exactly the same as 12edo, and a major-3rd ~4 cents smaller than 12edo: F# D 396.090 202 D Bb 300.000 153 B G D-minor has a minor-3rd intermediate between and 12edo and meantone, and a major-3rd a few cents wider than JI/meantone: A 390.225 199 F 305.865 156 D
Here is a graph comparing Werckmeister III with 1/4-comma meantone tuning:
The basic idea of this temperament is that every other "5th" is tuned 1/3 of a pythagorean comma narrow and the ones between them are tuned to the Pythagorean 3:2 ratio.
Werckmeister "5th" = (3/2) / ( ((2^-19)*(3^12))^(1/4) )
in monzo notation:
2^x * 3^y ~cents
[-1 1] 3:2 ratio = "perfect 5th" 701.9550009
- [-19/4 4] 1/3 Pythagorean-comma - 5.865002596
--------------- ---------------
[ 16/3 -3] Werckmeister #2 narrow 5th 694.1349974
2^x * 3^y ~cents
[-1 1] 3:2 ratio = "perfect 5th" 701.9550009
+ [-19/4 4] 1/3 Pythagorean-comma - 5.865002596
--------------- ---------------
[-22/3 5] Werckmeister #2 wide 5th 709.7750043
--"5th" size--
note comma --vector-- cents comma cents
mistuning 2 3 mistuning
G# -1&1/3 [17&1/3 -8] 784
> 0 702
C# -1&1/3 [18&1/3 -9] 82
> -1/3 694
F# -1 [13 -6] 588
> 0 702
B -1 [14 -7] 1086
> -1/3 694
E -2/3 [ 8&2/3 -4] 392
> 0 702
A -2/3 [ 9&2/3 -5] 890
> -1/3 694
D -1/3 [ 4&1/3 -2] 196
> 0 702
G -1/3 [ 5&1/3 -3] 694
> -1/3 694
C 0 [ 0 0] 0
> 0 702
F 0 [ 2 -1] 498
> -1/3 694
Bb +1/3 [-3&1/3 2] 1004
> +1/3 710
Eb 0 [ 4 -3] 294
> +1/3 710
G# -1&1/3 [11&1/3 -8] 784
Again, as in the Correct Temperament No. 1 above, the exponents of 2 for G# only signify 8ve-register, and have no effect on 8ve-invariant aspects of the tuning, signified by 3-8. Note also that Barbour's Table 136 (on p 160) has an error: the tuning of G# is given as 786 cents, but should be 784; the table above agrees with Barbour's description of this tuning as "containing 5 5ths flat by 1/3 comma, 2 5ths sharp by 1/3 comma, and 5 perfect 5ths".
The last tuning described by Werckmeister is known as the "Septenarius", because it is based on a string-length of 196 = 22 * 72. As Werckmeister himself wrote, this tuning is different from the three other "good" tunings because it is not based on a tempering by a division of the comma -- instead it is actually an example of an RI (rational-intonation) which is not a JI (just-intonation). In effect it is a well-temperament similar to the others, but created in a different way.
note string ------------ monzo ------------ ~cents name length ratio 2 3, 5 7 11, 13, 31,131,139 C 98 2/1 [ 1 0, 0 0 0, 0, 0, 0, 0> 1200.000 H 104 49/26 [-1 0, 0 2 0, -1, 0, 0, 0> 1097.124 B 110 98/55 [ 1 0, -1 2 -1, 0, 0, 0, 0> 1000.020 A 117 196/117 [ 2 -2, 0 2 0, -1, 0, 0, 0> 893.214 G# 124 49/31 [ 0 0, 0 2 0, 0, -1, 0, 0> 792.616 G 131 196/131 [ 2 0, 0 2 0, 0, 0, -1, 0> 697.544 F# 139 196/139 [ 2 0, 0 2 0, 0, 0, 0, -1> 594.923 F 147 4/3 [ 2 1, 0 0 0, 0, 0, 0, 0> 498.045 E 156 49/39 [ 0 -1, 0 2 0, -1, 0, 0, 0> 395.169 D# 165 196/165 [ 2 -1, -1 2 -1, 0, 0, 0, 0> 298.065 D 175 28/25 [ 2 0, -2 1 0, 0, 0, 0, 0> 196.198 C# 186 98/93 [ 1 -1, 0 2 0, 0, -1, 0, 0> 90.661 C 196 1/1 [ 0 0, 0 0 0, 0, 0, 0, 0> 0.000 NOTE: "D" was listed by Werckmeister as 176, but this is apparently an error and it should be 175.
see Tom Dent's webpage The Septenarius: Werckmeister's mythical tuning, made reality?, and Yahoo tuning message 60610
Werckmeister, Andreas. 1691.
Barbour, James Murray. 1951.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.