tonality diamond
An arbitrary arrangement of the Monophonic [musical frequency] ratios designed to constitute prima facie proof of the at least dual identity of each ratio, and consequently of the capacity of a Monophonic system of Just Intonation for providing tones that may be taken in more than one sense each.
Partch's Incipient Tonality Diamond (5-Limit):
(for a different view of this diamond, see the Monzo 5-Limit Lattice)
A chordal complex consisting of interlocking harmonic and subharmonic chords sharing a single tonic. It may be constructed by building replicas of a harmonic chord on roots that are the components of the octave inversion of the original. The highest prime (3, 5, 7, 11, etc.) number appearing in the chords determines the "limit".
The Diamond may be understood as the harmonic expansion of a single complex sound.
See Partch, Harry (1949, 1974, 1977).
When interpreted as a set of pitches instead of a set of intervals, the n-odd-limit is known as the "n-limit tonality diamond".
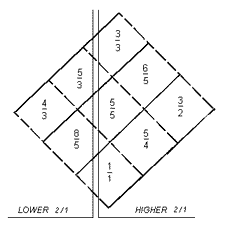
Illustrated below is an idea Joe Monzo had for a keyboard instrument, back around 1993. The buttons of the keyboard are arranged in a diamond, and the 50-cent boundaries between the 12-EDO scale are used to paint a pattern on the background similar to the usual Halberstadt pattern of black and white piano keys.
19-limit Tonality Diamond Keyboard idea, ©1993 by Joe Monzo

The pitches of a 19-odd-limit tonality diamond are laid out in Partch's diamond format, but arranged so that the otonal and utonal decads form ascending and descending scales, respectively. The red lines are otonal and the blue lines are utonal. The proportions of the scales are thus 16:17:18:19:(20=10):11:12:13:14:15.
The horizontal axis represents pitch-height exactly, so that a vertical column of buttons, viewed against the background of either a white or black "key", gives a precise view of all the different versions of any given 12-EDO pitch-class.
For example, looking down the row of buttons over the black "C#/Db key" just to the right of "middle-C" (a "white key" which runs down the exact center of the picture), from top to bottom, one can see:
15/14 = the 15-odentity of 8/7-otonality and
the 7-udentity of 15/8-utonality,
14/13 = the 7-odentity of 16/13-otonality and
the 13-udentity of 7/4-utonality,
13/12 = the 13-odentity of 4/3-otonality and
the 3-udentity of 13/8-utonality,
12/11 = the 3-odentity of 16/11-otonality and
the 11-udentity of 3/2-utonality,
20/19 = the 5-odentity of 32/19-otonality and
the 19-udentity of 5/4-utonality,
19/18 = the 19-odentity of 16/9-otonality and
the 9-udentity of 19/16-utonality,
18/17 = the 9-odentity of 32/17-otonality and
the 17-udentity of 9/8-utonality, and
17/16 = the 17-odentity of 1/1-otonality and
the 1-identity of 17/16-utonality,
and finally, if we look over at the lone C#/Db in the lower 2:1
("octave") of the keyboard (on the left side), we see:
16/15 = the 1-odentity of 16/15-otonality and
the 15-udentity of 1/1-utonality.
This gives a nice graphical presentation of all the different pitches falling between 0.50 and 1.50 Semitones (or 50 and 150 cents), which would have the following values in my 72-EDO-based HEWM notation, C = n^0 ,
Semitones ratio HEWM prime-factor ------- monzo -------
3 5 7 11 13 17 19
0.89 20/19 Db- 51 19-1 | 0 1 0 0 0 0 -1|
0.94 19/18 C# 3-2 191 |-2 0 0 0 0 0 1|
0.99 18/17 C# 32 17-1 | 2 0 0 0 0 -1 0|
1.05 17/16 Db 17-1 | 0 0 0 0 0 -1 0|
1.12 16/15 Db+ 3-1 5-1 |-1 -1 0 0 0 0 0|
1.19 15/14 C#+ 31 51 7-1 | 1 1 -1 0 0 0 0|
1.28 14/13 Db> 71 13-1 | 0 0 1 0 -1 0 0|
1.39 13/12 Db> 3-1 131 |-1 0 0 0 1 0 0|
1.51 12/11 Dv 31 11-1 | 1 0 0 -1 0 0 0|
where the accidentals have the following meaning:
^ +1/4-tone > + <6th-t>1/6-tone + + <12th-t>1/12-tone 0 - - 1/12-tone < - 1/6-tone v - 1/4-tone
And so on for all the other "black and white keys". The only "key" or pitch-class having only one pitch is C = n0.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
