LucyTuning
and 88-ed2 / 88-edo / 88-ET / 88-tone equal-temperament, and 3/10-comma meantone
LucyTuning is a tuning invented by John 'Longitude' Harrison in the 1700s and rediscovered and promoted currently by Charles Lucy. It is a type of meantone composed of two different step sizes (designated L and s) such that 5L + 2s = one octave, as in many familiar diatonic scales.
The Large interval (L) is the "whole-tone" (IInd), with the ratio 2π√2 ("the two pi root of two") or 2(1 / 2π) = ~1.116633. That is 1200 / 2π cents = ~190.9858 cents.
The small interval (s) is half the difference between 5 Large intervals and one octave, i.e. (8ve - 5L) / 2 , and is the "flat second" (bIInd), with the ratio (2 / 2(5 / 2π))(1/2) = ~1.073344. That is s = ~122.5354 cents.
LucyTuning has a "5th" or generator at the "low end" of the meantone spectrum, with an interval size between that of 1/3-comma meantone and Zarlino's 2/7-comma meantone (see the right side of the graph at the bottom of the meantone entry).
This generator or "5th" is composed of three Large (3L) plus one small note (s), i.e. (3L+s) = (~190.986*3) + (~122.535) = ~695.493 cents or ratio of
2(3 / 2π) * (2 / 2(5 / 2π))(1/2) = 2(2π + 1) / 4π, or 2(1/2 + 1/4π) = ~1.49441151.
Note that the size of the LucyTuning "5th" can also be expressed logarithmically as 600+(300/π) cents.
The LucyTuning "major-3rd" has the ratio 2(1/π) = ~1.246868989 = ~381.9718634 cents.
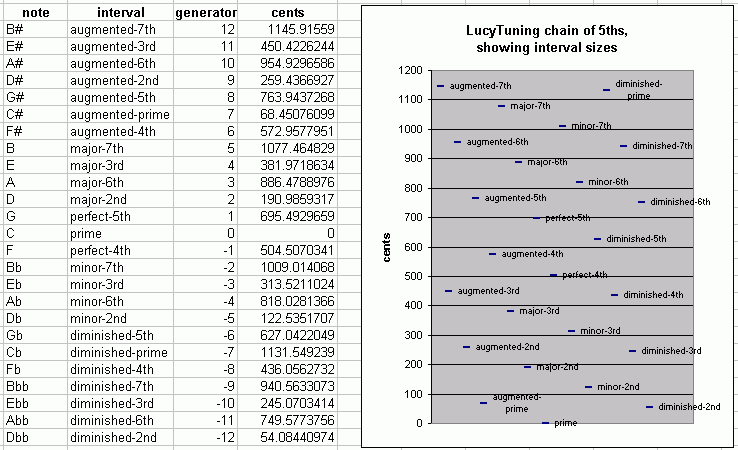
Below is a table and graph showing a 25-tone LucyTuning chain of 5ths, with all the intervals normally found in common-practice harmony labeled.
3/10-comma meantone
The LucyTuning generator "5th" is audibly indistinguishable from that of 3/10-comma meantone:
22/10 * 3-2/10 * 53/10 3/10-comma meantone "5th" - 2(2π+1)/4π Lucytuning "5th" --------------------------------- 2(-12π-10)/40π * 3-2/10 * 53/10 = ~0.010148131 cent = ~1/99 cent
88-edo
Carrying the LucyTuning meantone chain out to the 88th generator results in a pitch ~3.380995252 cents higher than the starting pitch. If the chain is centered on the origin (i.e., divided as equally as possible on the "flat" and "sharp" sides), and carried out to 12, 19, or 31 generators (typical sizes of meantone chains), the maximum differences of 88-edo from LucyTuning are respectively ~2/9, ~1/3, and ~4/7 of a cent. Therefore, for most purposes LucyTuning and 88-edo are essentially the same.
2(2π+1)/4π Lucytuning "5th" - 251/88 88edo "5th" ---------------- 2(-7π+22)/88π = ~0.038420401 cent = ~1/26 cent
Even a 101-tone LucyTuning chain of 5ths will still present less than 2 cents error from 88edo, as shown in the table below:
---------------- cents ---------------------
generator LucyTuning 88-edo error
50 1174.648293 1172.727273 - 1.92102003
49 479.1553269 477.2727273 - 1.882599629
48 983.662361 981.8181818 - 1.844179228
47 288.1693952 286.3636364 - 1.805758828
46 792.6764293 790.9090909 - 1.767338427
45 97.18346348 95.45454545 - 1.728918027
44 601.6904976 600.0000000 - 1.690497626
43 1106.197532 1104.545455 - 1.652077225
42 410.7045659 409.0909091 - 1.613656825
41 915.2116001 913.6363636 - 1.575236424
40 219.7186342 218.1818182 - 1.536816024
39 724.2256684 722.7272727 - 1.498395623
38 28.7327025 27.27272727 - 1.459975222
37 533.2397366 531.8181818 - 1.421554822
36 1037.746771 1036.363636 - 1.383134421
35 342.2538049 340.9090909 - 1.344714021
34 846.7608391 845.4545455 - 1.30629362
33 151.2678732 150.0000000 - 1.26787322
32 655.7749074 654.5454545 - 1.229452819
31 1160.281942 1159.090909 - 1.191032418
30 464.7889757 463.6363636 - 1.152612018
29 969.2960098 968.1818182 - 1.114191617
28 273.8030439 272.7272727 - 1.075771217
27 778.3100781 777.2727273 - 1.037350816
26 82.81711223 81.81818182 - 0.998930415
25 587.3241464 586.3636364 - 0.960510015
24 1091.831181 1090.909091 - 0.922089614
23 396.3382147 395.4545455 - 0.883669214
22 900.8452488 900.0000000 - 0.845248813
21 205.352283 204.5454545 - 0.806828412
20 709.8593171 709.0909091 - 0.768408012
19 14.36635125 13.63636364 - 0.729987611
18 518.8733854 518.1818182 - 0.691567211
17 1023.38042 1022.727273 - 0.65314681
16 327.8874537 327.2727273 - 0.614726409
15 832.3944878 831.8181818 - 0.576306009
14 136.901522 136.3636364 - 0.537885608
13 641.4085561 640.9090909 - 0.499465208
12 1145.91559 1145.454545 - 0.461044807
11 450.4226244 450.0000000 - 0.422624407
10 954.9296586 954.5454545 - 0.384204006
9 259.4366927 259.0909091 - 0.345783605
8 763.9437268 763.6363636 - 0.307363205
7 68.45076099 68.18181818 - 0.268942804
6 572.9577951 572.7272727 - 0.230522404
5 1077.464829 1077.272727 - 0.192102003
4 381.9718634 381.8181818 - 0.153681602
3 886.4788976 886.3636364 - 0.115261202
2 190.9859317 190.9090909 - 0.076840801
1 695.4929659 695.4545455 - 0.038420401
0 0.0000000 0.0000000 0.000000000
-1 504.5070341 504.5454545 + 0.038420401
-2 1009.014068 1009.090909 + 0.076840801
-3 313.5211024 313.6363636 + 0.115261202
-4 818.0281366 818.1818182 + 0.153681602
-5 122.5351707 122.7272727 + 0.192102003
-6 627.0422049 627.2727273 + 0.230522404
-7 1131.549239 1131.818182 + 0.268942804
-8 436.0562732 436.3636364 + 0.307363205
-9 940.5633073 940.9090909 + 0.345783605
-10 245.0703414 245.4545455 + 0.384204006
-11 749.5773756 750.0000000 + 0.422624407
-12 54.08440974 54.54545455 + 0.461044807
-13 .558.5914439 559.0909091 + 0.499465208
-14 1063.098478 1063.636364 + 0.537885608
-15 367.6055122 368.1818182 + 0.576306009
-16 872.1125463 872.7272727 + 0.614726409
-17 176.6195805 177.2727273 + 0.65314681
-18 681.1266146 681.8181818 + 0.691567211
-19 1185.633649 1186.363636 + 0.729987611
-20 490.1406829 490.9090909 + 0.768408012
-21 994.647717 995.4545455 + 0.806828412
-22 299.1547512 300.0000000 + 0.845248813
-23 803.6617853 804.5454545 + 0.883669214
-24 108.1688195 109.0909091 + 0.922089614
-25 612.6758536 613.6363636 + 0.960510015
-26 1117.182888 1118.181818 + 0.998930415
-27 421.6899219 422.7272727 + 1.037350816
-28 926.1969561 927.2727273 + 1.075771217
-29 230.7039902 231.8181818 + 1.114191617
-30 735.2110243 736.3636364 + 1.152612018
-31 39.71805849 40.90909091 + 1.191032418
-32 544.2250926 545.4545455 + 1.229452819
-33 1048.732127 1050.000000 + 1.26787322
-34 353.2391609 354.5454545 + 1.30629362
-35 857.7461951 859.0909091 + 1.344714021
-36 162.2532292 163.6363636 + 1.383134421
-37 666.7602634 668.1818182 + 1.421554822
-38 1171.267298 1172.727273 + 1.459975222
-39 475.7743316 477.2727273 + 1.498395623
-40 980.2813658 981.8181818 + 1.536816024
-41 284.7883999 286.3636364 + 1.575236424
-42 789.2954341 790.9090909 + 1.613656825
-43 93.80246823 95.45454545 + 1.652077225
-44 598.3095024 600.0000000 + 1.690497626
-45 1102.816537 1104.545455 + 1.728918027
-46 407.3235707 409.0909091 + 1.767338427
-47 911.8306048 913.6363636 + 1.805758828
-48 216.337639 218.1818182 + 1.844179228
-49 720.8446731 722.7272727 + 1.882599629
-50 25.35170724 27.27272727 + 1.92102003
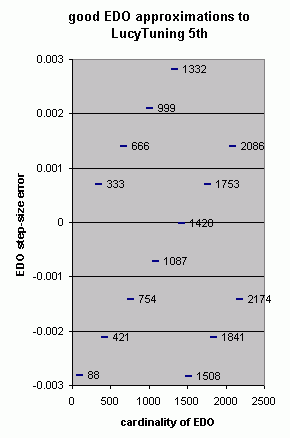
88-edo is the lowest cardinality EDO which gives a very good approximation to LucyTuning. 1420-edo is an extremely good approximation, as can be seen in the graph below, which shows the error of the EDO 5th from the LucyTuning 5th as a percentage of that EDO's step size, for several EDOs which give a better approximation than 88-edo.
See the LucyTuning homepage for more information.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.
