tina
A very small unit of interval measurement, advocated by Joe Monzo primarly because of its accuracy for use as logarithmic integer values to describe just-intonation intervals thru the 31-limit, first suggested by privately by George Secor in September 2004, then publicly by Gene Ward Smith on 22 April 2007. A few days later, Monzo independently found, by using an error calculation that weighted the percent error for prime-factors as 3:*10, 5:*6, 7:*3, 11:*2, and all the others up to 41 *1, that 8539-edo had a lower "score" than any other EDO with cardinality smaller than 19932-edo, giving excellent approximations to all primes in the 41-limit except 37. Dave Keenan and George Secor referred to it as "tina", a name which Monzo adopted.
A tina divides the octave into 8,539 equal parts. Because that number is prime, it does not offer any other divisibility, which is its chief disadvantage.
The tina is therefore calculated as the 8539th root of 2, or 2(1/8539), with a ratio of approximately 1:1.000081178. It is an irrational number.
A tina is:
- exactly 12/8539 (= ~0.001405 = ~ 1/712 ) of a 12-edo semitone,
- exactly 19/8539 (= ~0.002225 = ~ 1/449 ) of a 19-edo "third-tone",
- exactly 31/8539 (= ~0.003630 = ~ 1/275 ) of a 31-edo diesis,
- exactly 43/8539 (= ~0.005036 = ~ 1/199 ) of a 43-edo méride,
- exactly 53/8539 (= ~0.006207 = ~ 1/161 ) of a 53-edo mercator,
- exactly 72/8539 (= ~0.008432 = ~ 1/119 ) of a 72-edo morion,
- exactly 144/8539 (= ~0.016864 = ~ 1/59 ) of a 144-edo farab,
- exactly 300/8539 (= ~0.035133 = ~ 1/28 ) of a 300-edo savart,
- exactly 301/8539 (= ~0.035250 = ~ 1/28 ) of a 301-edo heptaméride,
- exactly 612/8539 (= ~0.071671 = ~ 1/14 ) of a 612-edo sk,
- approximately 0.071883 (= ~ 1/14 ) of a grad,
- exactly 730/8539 (= ~0.085490 = ~ 1/12 ) of a 730-edo woolhouse-unit,
- exactly 768/8539 (= ~0.089940 = ~ 1/11 ) of a 768-edo 6mu,
- exactly 1000/8539 (= ~0.117110 = ~ 1/9 ) of a 1000-edo millioctave,
- exactly 1024/8539 (= ~0.119920 = ~ 1/8 ) of a 1024-edo yamaha-unit,
- exactly 1200/8539 (= ~0.140532 = ~ 1/7 ) of a 1200-edo cent,
- exactly 2460/8539 (= ~0.288090 = ~ 2/7 ) of a 2460-edo mina,
- exactly 1 2061/8539 (= ~1.241363 = ~ 1 1/4 ) 10600-edo türk-sents,
- exactly 3 4486/8539 (= ~3.525354 = ~ 3 1/2 ) 30103-edo jots,
- approximately 4.312991 (= ~ 4 1/3 ) tuning-units,
- exactly 5 3337/8539 (= ~5.390795 = ~ 5 2/5 ) 46032-edo flus,
- exactly 5 6457/8539 (= ~5.756178 = ~ 5 3/4 ) 49152-edo 12mus,
- exactly 6 7739/8539 (= ~6.906312 = ~ 6 10/11 ) 58973-edo units,
- exactly 23 211/8539 (= ~23.024710 = ~ 23 1/40 ) 196608-edo 14mus,
The formula for calculating the tina-value of any ratio r is: tinas = log10(r) * [ 8539 / log10(2) ] or tinas = log2(r) * 8539
A tina represents one degree of 8539-edo tuning.
The 12-edo semitone is exactly 711 7/12 (= 711.58,3...) tinas, a value which is nearly midway between two adjacent tinas. The unfortunate result of this is that there is rounding error when using tinas to represent 12-edo. In actual practice it is not really a problem because one tina is so small, but it does cause problems with the mathematics. Below is a table (arranged in descending order of pitch) showing the tina values for 12-edo based on the chain-of-5ths from -5...+6 generators:
12edo s-t .. tinas 12 .. 8539 11 .. 7827 10 .. 7116 9 .. 6404 8 .. 5693 7 .. 4981 6 .. 4269 5 .. 3558 4 .. 2846 3 .. 2135 2 .. 1423 1 ... 712 0 ..... 0
Below is a table of tina values for common 31-limit JI interval sizes; tina values are given both in integer and floating-point form, expressly to point out how unnecessary it is to use the decimal places for most of the cases:
integer floating-pt ------------- monzo ---------------
interval name tinas tinas 2 3, 5 7 11, 13 17 19, 23 29 31 ratio
octave .............................. 8539 8539.00 [ 1> ...................................... 1/1
8386 8385.96 [ 5 -4, 1> ............................ 160/81
8345 8344.99 [ -5 2, 0 1> .......................... 63/32
8247 8246.83 [ -6 0, 3> ............................ 125/64
8160 8159.92 [ 6 -1, 0 0 -1> ....................... 64/33
31st harmonic ....................... 8148 8147.88 [ -4 0, 0 0 0, 0 0 0, 0 0 1> ... 31/16
septimal major-7th .................. 8091 8090.98 [ -1 3, 0 -1> .......................... 27/14
8068 8068.15 [ -3 0, -1 1 1> ....................... 77/40
8036 8036.11 [ 4 1, -2> ............................. 48/25
7938 7937.95 [ 3 -1, 1 -1> .......................... 40/21
pyth major-7th ...................... 7897 7896.97 [ -7 5> ................................ 243/128
7883 7883.07 [ 8 -3, -1> ............................ 256/135
7814 7814.13 [ 1 1, -1 -1 1>........................ 66/35
17th subharmonic .................... 7792 7792.15 [ 5 0, 0 0 0, 0 -1> ................ 32/17
just major-7th / 15th harmonic ..... 7744 7743.94 [ -3 1, 1> ............................. 15/8
7730 7730.04 [ 12 -7> ............................... 4096/2187
7689 7689.06 [ 2 -1, -1 1> .......................... 28/15
undecimal neutral-7th ............... 7467 7467.09 [ -1 -1, 0 0 1> ....................... 11/6
7435 7435.05 [ 6 0, -1 -1> .......................... 64/35
7365 7364.86 [ 2 0, 1 0 -1 ........................ 20/11
29th harmonic ....................... 7326 7326.30 [ -4 0, 0 0 0, 0 0 0, 0 1> ...... 29/16
7273 7273.09 [ -7 1, 0 1 1> ...................... 231/128
pyth aug-6th ....................... 7255 7254.95 [-15 10> .............................. 59049/32768
just minor-7th ...................... 7241 7241.05 [ 0 2, -1> .............................. 9/5
7102 7101.91 [-11 6, 1> ........................... 3645/2048
pyth minor-7th / 9th subharmonic .... 7088 7088.01 [ 4 -2> ................................. 16/9
just aug-6th ........................ 6949 6948.88 [ -7 2, 2> ............................ 225/128
7th harmonic ........................ 6894 6894.00 [ -2 0, 0 1> ........................... 7/4
septimal minor-7th .................. 6894 6894.00 [ -2 0, 0 1> ........................... 7/4
6862 6861.96 [ 5 1, -1 0 -1 ........................ 96/55
6672 6672.03 [ -5 0, 1 0 1 ........................ 55/32
septimal major-6th .................. 6640 6639.99 [ 2 1, 0 -1> .......................... 12/7
6599 6599.02 [ -8 7, -1> ........................... 2187/1280
6585 6585.12 [ 7 -1, -2> ............................ 128/75
pyth major-6th / 27th harmonic ..... 6446 6445.98 [ -4 3> ................................. 27/16
19th subharmonic .................... 6422 6421.95 [ 5 0, 0 0 0, 0 0 -1> ............. 32/19
6363 6363.14 [ 4 -1, -1 -1 1> ...................... 176/105
just major-6th ...................... 6293 6292.95 [ 0 -1, 1> .............................. 5/3
6169 6169.14 [ -2 1, -1 0 1> ....................... 33/20
6099 6098.94 [ -6 1, 1 1> ......................... 105/64
6067 6066.90 [ 1 2, 0 0 -1> ....................... 18/11
13th harmonic ....................... 5981 5981.05 [ -3 0, 0 0 0, 1> ................... 13/8
5822 5822.10 [ -4 -1, 0 1 1> ....................... 77/48
pyth aug-5th ....................... 5804 5803.96 [-12 8> ............................... 6561/4096
just minor-6th / 5th subharmonic .... 5790 5790.06 [ 3 0, -1> .............................. 8/5
5651 5650.92 [ -8 4, 1> ............................ 405/256
pyth minor-6th ...................... 5637 5637.02 [ 7 -4> ................................ 128/81
5568 5568.08 [ 0 0, 0 -1 1> ....................... 11/7
just aug-5th ........................ 5498 5497.89 [ -4 0, 2> ............................. 25/16
5443 5443.01 [ 1 -2, 0 1> .......................... 14/9
5411 5410.97 [ 8 -1, -1 0 -1> ...................... 256/165
5374 5374.08 [ -6 2, 0 0 1> ....................... 99/64
septimal 5th / 21st subharmonic ..... 5189 5189.00 [ 5 -1, 0 -1> .......................... 32/21
5148 5148.03 [ -5 5, -1> ............................ 243/160
perfect-5th / 3rd harmonic .......... 4995 4994.99 [ -1 1> .................................. 3/2
just wolf-5th ....................... 4842 4841.96 [ 3 -3, 1> ............................. 40/27
4801 4800.99 [ -7 3, 0 1> ......................... 189/128
4718 4718.15 [ 1 -1, -1 0 1> ....................... 22/15
4703 4702.83 [ -8 1, 3> ............................ 375/256
4648 4647.95 [ -3 -1, 1 1> .......................... 35/24
11th subharmonic .................... 4616 4615.91 [ 4 0, 0 0 -1> ....................... 16/11
4524 4524.14 [ -5 1, -1 1 1> ...................... 231/160
large just dim-5th .................. 4492 4492.10 [ 2 2, 2> ............................. 36/25
23rd harmonic ....................... 4471 4470.70 [ -4 0, 0 0 0, 0 0 0, 1> ......... 23/16
septimal aug-4th .................... 4394 4393.94 [ 1 0, 1 -1> .......................... 10/7
pyth aug-4th / tritone .............. 4353 4352.97 [ -9 6> ................................ 729/512
small just dim-5th .................. 4339 4339.07 [ 6 -2, -1> ............................. 64/45
just aug-4th / tritone .............. 4200 4199.93 [ -5 2, 1> ............................. 45/32
pyth dim-5th ........................ 4186 4186.03 [ 10 -6> ............................... 1024/729
septimal dim-5th .................... 4145 4145.06 [ 0 0, -1 1> ........................... 7/5
23rd subharmonic .................... 4068 4068.30 [ 5 0, 0 0 0, 0 0 0, -1> ......... 32/23
4047 4046.90 [ -1 -2, 2> ............................. 25/18
11th harmonic ....................... 3923 3923.09 [ -3 0, 0 0 1> ....................... 11/8
3891 3891.05 [ 4 1, -1 -1> .......................... 48/35
3836 3836.17 [ 9 -1, -3> ............................ 512/375
3821 3820.85 [ 0 1, 1 0 -1> ....................... 15/11
3711 3710.94 [-17 11> ............................. 177147/131072
3697 3697.04 [ -2 3, -1> ............................. 27/20
3558 3557.91 [-13 7> .............................. 10935/8192
perfect-4th / 3rd subharmonic ....... 3544 3544.01 [ 2 -1> .................................. 4/3
3405 3404.87 [ -9 3> ................................ 675/512
septimal-4th / 21st harmonic ........ 3350 3350.00 [ -4 1, 0 1> .......................... 21/16
3252 3251.84 [ -5 -1, 3> ............................ 125/96
3165 3164.92 [ 7 -2, 0 0 -1> ...................... 128/99
3128 3128.03 [ -7 1, 1 0 1> ...................... 165/128
septimal major-3rd .................. 3096 3095.99 [ 0 2, 0 -1> ........................... 9/7
3073 3073.15 [ -2 -1, -1 1 1> ....................... 77/60
3041 3041.11 [ 5 0, -2> ............................. 32/25
pyth major-3rd / ditone ............. 2902 2901.98 [ -6 4> ................................. 81/64
2888 2888.08 [ 9 -4, -1> ............................ 512/405
2819 2819.14 [ 2 0, -1 -1 1> ....................... 44/35
just major-3rd / 5th harmonic ..... 2749 2748.94 [ -2 0, 1> .............................. 5/4
13th subharmonic .................... 2558 2557.95 [ 4 0, 0 0 0, -1> ................... 16/13
undecimal neutral-3rd ............... 2472 2472.10 [ 0 -2, 0 0 1> ....................... 11/9
2440 2440.06 [ 7 -1, -1 -1> ......................... 128/105
2370 2369.86 [ 3 -1, 1 0 -1> ....................... 40/33
2278 2278.09 [ -6 0, 0 1 1> ....................... 77/64
pyth aug-2nd ........................ 2260 2259.95 [-14 9> .............................. 19683/16384
just minor-3rd ...................... 2246 2246.05 [ 1 1, -1> .............................. 6/5
19th harmonic ....................... 2117 2117.05 [ -4 0, 0 0 0, 0 0 1> ............. 19/16
2107 2106.92 [-10 5, 1> ........................... 1215/1024
pyth minor-3rd / trihemitone ........ 2093 2093.02 [ 5 -3> ................................. 32/27
2024 2024.08 [ -2 1, 0 -1 1> ....................... 33/28
1954 1953.88 [ -6 1, 2> ............................. 75/64
septimal minor-3rd .................. 1899 1899.01 [ -1 -1, 0 1> ........................... 7/6
1867 1866.97 [ 6 0, -1 0 -1> ....................... 64/55
1677 1677.04 [ -4 -1, 1 0 1> ....................... 55/48
septimal major-2nd / 7th subharmonic 1645 1645.00 [ 3 0, 0 -1> ........................... 8/7
1604 1604.02 [ -7 6, -1> ............................ 729/640
pyth major-2nd / tone / 9th harmonic 1451 1450.99 [ -3 2> .................................. 9/8
just minor-2nd / small tone ......... 1298 1297.95 [ 1 -2, 1> ............................. 10/9
29th subharmonic .................... 1213 1212.70 [ 5 0, 0 0 0, 0 0 0, 0 -1> ...... 32/29
1174 1174.14 [ -1 0, -1 0 1> ....................... 11/10
1104 1103.95 [ -5 0, 1 1> .......................... 35/32
1072 1071.91 [ 2 1, 0 0 -1> ....................... 12/11
948 948.10 [ 0 3, -2> ............................. 27/25
850 849.94 [ -1 1, 1 -1> .......................... 15/14
pyth aug-prime / apotome ............ 809 808.96 [-11 7> ............................... 2187/2048
just minor-2nd / 15th subharmonic ... 795 795.06 [ 4 -1, -1> ............................. 16/15
17th harmonic ....................... 747 746.85 [ -4 0, 0 0 0, 0 1> ................ 17/16
large just aug-prime ................ 656 655.93 [ -7 3, 1> ............................ 135/128
pyth minor-2nd / limma .............. 642 642.03 [ 8 -5> ................................ 256/243
601 601.05 [ -2 1, -1 1> .......................... 21/20
573 573.09 [ 1 -1, 0 -1 1> ....................... 22/21
small just aug-prime ................ 503 502.89 [ -3 -1, 2> ............................. 25/24
pyth tricomma ...................... 501 500.81 [-57 36> ........................... 1.50E+17/1.44E+17
31st subharmonic .................... 391 391.12 [ 5 0, 0 0 0, 0 0 0, 0 0 -1> .. 32/31
undecimal-diesis / 33rd harmonic .... 379 379.08 [ -5 1, 0 0 1> ....................... 33/32
maximal-diesis ...................... 350 349.86 [ 1 -5, 3> ............................ 250/243
septimal-diesis ..................... 347 347.04 [ 2 2, -1 -1> .......................... 36/35
enharmonic diesis ................... 292 292.17 [ 7 0, -3> ............................ 128/125
large biseptimal-comma .............. 254 254.01 [ -4 -1, 0 2> .......................... 49/48
small biseptimal-comma .............. 249 248.88 [ 1 0, 2 -2> .......................... 50/49
magic-comma ........................ 211 210.73 [-10 -1, 5> ........................... 3125/3072
septimal comma ...................... 194 194.01 [ 6 -2, 0 -1> .......................... 64/63
pythagorean-comma .................. 167 166.94 [-19 12> ............................. 531441/524288
syntonic-comma ...................... 153 153.04 [ -4 4, -1> ............................. 81/80
diaschisma .......................... 139 139.13 [ 11 -4, -2> ........................... 2048/2025
semicomma .......................... 72 71.59 [-21 3, 7> ........................ 2109375/2097152
kleisma ............................. 58 57.69 [ -6 -5, 6> .......................... 15625/15552
septimal-kleisma .................... 55 54.87 [ -5 2, 2 -1> ......................... 225/224
septimal-schisma .................... 27 27.07 [ 25 -14, 0 -1> .................... 33554432/33480783
mercator-comma ..................... 26 25.72 [-84 53> ........................... 1.94E+25/1.93E+25
nondecimal-schisma .................. 24 24.04 [ -9 3, 0 0 0, 0 0 1> ............ 513/512
skhisma ............................ 14 13.90 [-15 8, 1> .......................... 32805/32768
monzisma ............................ 2 2.08 [ 54 -37, 2> ....................... 4.50E+17/4.50E+17
nanisma ............................ 1 1.35 [109 -67, 0 -1> .................... 6.49E+32/6.49E+32
origin / prime / unison ............. 0 0.00 [ 0> ...................................... 1/1
Out of the 148 intervals listed in this table, only 9 have an error of around 30 percent or more (listed here in order of decreasing error):
interval ......... tinas .. percent error semicomma ........... 72 .. 41 nanisma .............. 1 .. 35 kleisma ............. 58 .. 31 23rd subharmonic .. 4068 .. 30 29th harmonic ..... 7326 .. 30 23rd harmonic ..... 4471 .. 30 29th subharmonic .. 1213 .. 30 mercator-comma ...... 26 .. 28 magic-comma ........ 211 .. 27
Of those, the only really important ones for most people will be the semicomma, kleisma, and magic-comma. All the rest of the JI intervals in the table (except one) have an error of 17 percent or less. This a remarkably low level of error for an integer logarithmic measurement unit.
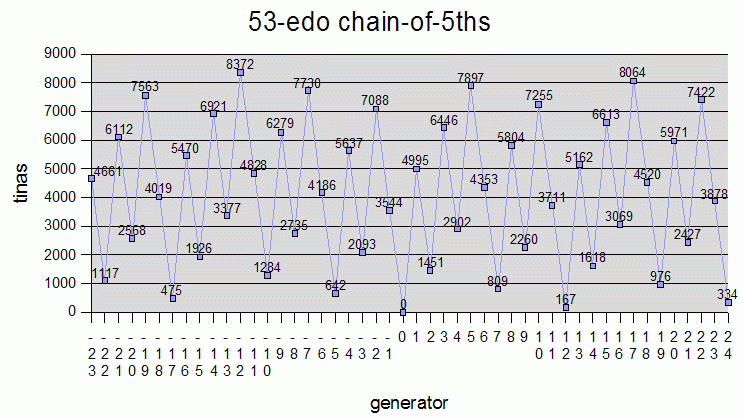
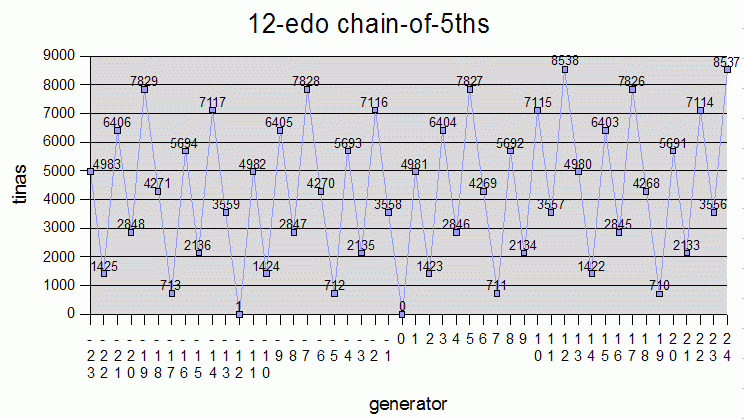
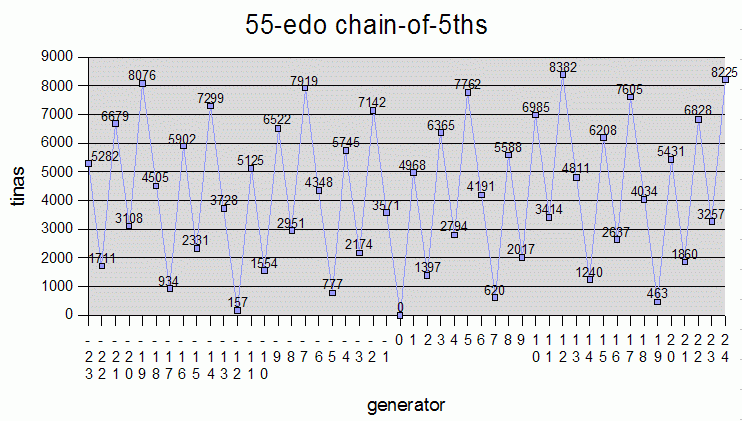
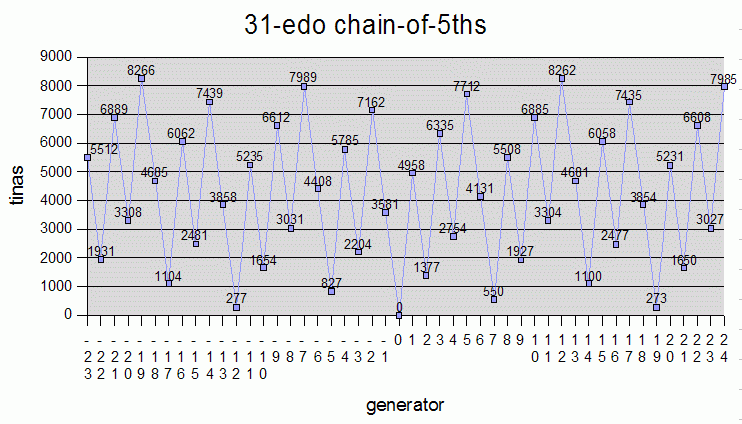
Below is a table of the tina values for all of the commonly used intervals, in all of the standard keys, in some of the most important EDO meantones. The intervals are listed as a chain-of-5ths, in decreasing generator order, with the tonic of each key as the zeroth generator. 53-edo is also shown for comparison, as a representation of pythagorean tuning. The percentage errors for 12-, 55-, and 31-edo are quite low, those for 43-, 50-, and 19-edo not as good, and the error for 53-edo almost as bad as it can get, at 49% (i.e., the 5th of 53-edo is almost midway between two tina values, at ~4994.5094) -- the values shown in the 53-edo column are actually quite accurate for real pythagorean JI tuning.
EDOs ---------------------------------
.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. generator 53 12 55 43 31 50 19
.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. Ax . 24 .. 334 8537 8225 8153 7985 7865 7649
.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. Ax .Dx . 23 . 3878 3556 3257 3188 3027 2912 2705
.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx . 22 . 7422 7114 6828 6762 6608 6498 6300
.. .. .. .. .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx . 21 . 2427 2133 1860 1797 1650 1545 1356
.. .. .. .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx . 20 . 5971 5691 5431 5371 5231 5131 4951
dbl aug-7th ..... .. .. .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# . 19 . 976 710 463 406 273 178 7
dbl aug-3rd ..... .. .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# . 18 . 4520 4268 4034 3980 3854 3764 3602
dbl aug-6th ..... .. .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# . 17 . 8064 7826 7605 7554 7435 7350 7197
dbl aug-2nd ..... .. .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# . 16 . 3069 2845 2637 2589 2477 2397 2253
dbl aug-5th ..... .. .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# . 15 . 6613 6403 6208 6163 6058 5983 5848
dbl aug-prime .. .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# . 14 . 1618 1422 1240 1198 1100 1030 904
dbl aug-4th .. .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# . 13 . 5162 4980 4811 4772 4681 4616 4499
aug-7th ........ .. .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B .. 12 .. 167 8538 8382 8346 8262 8202 8094
aug-3rd ........ .. .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E .. 11 . 3711 3557 3414 3381 3304 3249 3150
aug-6th ........ .. .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A .. 10 . 7255 7115 6985 6955 6885 6835 6745
aug-2nd ........ .. .. Ax .Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D .. 9 . 2260 2134 2017 1990 1927 1882 1801
aug-5th ........ Ax. Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G .. 8 . 5804 5692 5588 5564 5508 5468 5396
Chromatic s-t ...Ax Dx .Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C .. 7 . 809 711 620 599 550 515 452
aug-4th ........ Dx Gx .Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F .. 6 . 4353 4269 4191 4173 4131 4101 4047
major-7th ...... Gx Cx .Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb . 5 . 7897 7827 7762 7747 7712 7687 7642
major-3rd ...... Cx Fx .B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb . 4 . 2902 2846 2794 2782 2754 2734 2698
major-6th ...... Fx B# .E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab . 3 . 6446 6404 6365 6356 6335 6320 6293
major-2nd ...... B# E# .A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db . 2 . 1451 1423 1397 1391 1377 1367 1349
perfect-5th .....E# A# .D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb . 1 . 4995 4981 4968 4965 4958 4953 4944
Prime .......... A# D# .G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb . 0 .. 0 0 0 0 0 0 0
perfect-4th .... D# G# .C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb . -1 . 3544 3558 3571 3574 3581 3586 3595
minor-7th .......G# C# .F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb -2 . 7088 7116 7142 7148 7162 7172 7190
minor-3rd ...... C# F# .B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb -3 . 2093 2135 2174 2183 2204 2219 2246
minor-6th .......F# B ..E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb -4 . 5637 5693 5745 5757 5785 5805 5841
Diatonic s-t .. B E ..A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb -5 .. 642 712 777 792 827 852 897
dim-5th ........ E A ..D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb -6 . 4186 4270 4348 4366 4408 4438 4492
dim-8ve ....... A D ..G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. -7 . 7730 7828 7919 7940 7989 8024 8087
dim-4th ........ D G ..C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. -8 . 2735 2847 2951 2975 3031 3071 3143
dim-7th ........ G C ..F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. -9 . 6279 6405 6522 6549 6612 6657 6738
dim-3rd ....... C F ..Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. -10 1284 1424 1554 1584 1654 1704 1794
dim-6th ....... F Bb .Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. -11 4828 4982 5125 5158 5235 5290 5389
dim-2nd ....... Bb Eb .Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. -12 8372 1 157 193 277 337 445
dbl dim-5th ... Eb Ab .Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. -13 3377 3559 3728 3767 3858 3923 4040
dbl dim-8ve ... Ab Db .Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. -14 6921 7117 7299 7341 7439 7509 7635
dbl dim-4th ... Db Gb .Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. -15 . 1926 2136 2331 2376 2481 2556 2691
dbl dim-7th ... Gb Cb .Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. -16 . 5470 5694 5902 5950 6062 6142 6286
dbl dim-3rd ... Cb Fb .Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. -17 475 713 934 985 1104 1189 1342
dbl dim-6th ... Fb Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. .. -18 4019 4271 4505 4559 4685 4775 4937
dbl dim-2nd ... Bbb Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. .. .. -19 7563 7829 8076 8133 8266 8361 8532
Ebb Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. .. .. .. -20 2568 2848 3108 3168 3308 3408 3588
Abb Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. -21 6112 6406 6679 6742 6889 6994 7183
Dbb Gbb .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. -22 1117 1425 1711 1777 1931 2041 2239
Gbb .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. -23 4661 4983 5282 5351 5512 5627 5834
Below are graphs of the tina-values for some of the EDO chain-of-5ths tunings in the above table:
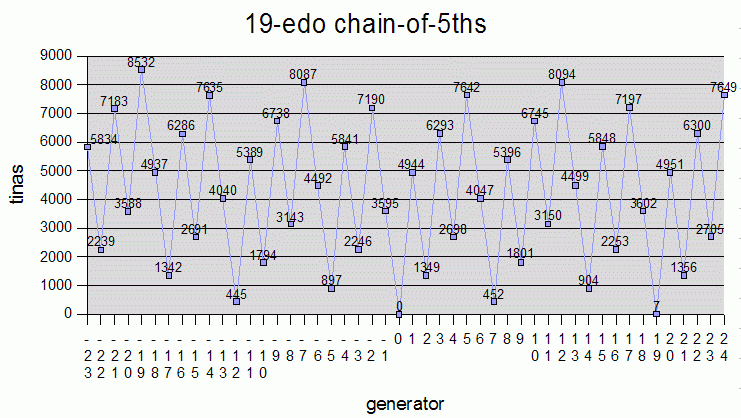
tinas calculator
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
