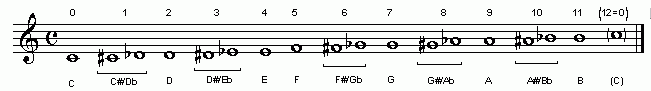
The usual and familiar 12-tone equal-tempered scale, the standard scale tuning used on keyboard, fretted string, and woodwind and brass instruments. This tuning assumes an equivalence-interval of 2:1 frequency ratio (called the "octave"), the pitch-space of which is logarithmically divided into 12 equal intervals called semitones.
The musical illustration at the top of this page shows the 12-edo degree numbers above the music notes (shown here as 1 - 12, they are actually usually numbered by theorists from 0 - 11), and the letter-name nominals below. Note that there are brackets connecting certain pairs of notes with the paired nominals below (i.e., C#/Db etc.). These pairs of notes, which are "spelled" differently but have exactly the same pitch in 12-edo, are termed "enharmonically equivalent" ... the explanation of this will unfold below.
12-edo tuning is calculated by taking the twelfth root of each successive power of 2, from 0 to 11; higher or lower "octaves" of these 12 notes are assumed to be, and are tuned as, equivalents. The 12th root of 2 can also be written as 2(1/12), the next degree, the 12th root of 22, as 2(2/12), etc. The latter of each pair are the form of notation normally used in internet discourse, and in this Encyclopaedia; in books and journals published in hard-copy one more often finds the use of the surd (√) with an index indicating the equal division (in this case, 12). Any number to the 0th power equals 1, so the starting note of the scale, or 2(0/12), has the ratio 1:1. Exponents which have numerators which are multiples of 12 form "octaves", as in the following:
| 2(12/12) = 21 = the ratio 2:1 = the "octave" |
| 2(24/12) = 22 = the ratio 4:1 = 2 "octaves" |
| 2(36/12) = 23 = the ratio 8:1 = 3 "octaves" |
These proportions -- the origin and its octaves -- are obviously all powers of 2. All other divisions in this scale are proportions known as irrational numbers.
As a result of the mathematical complexity, this scale was never tuned with absolute precision, with the exception of the "octaves" of the starting-note, until just a few decades ago, with the introduction of electronic and digital instruments and tuners. However, Monzo speculates that as long ago as 3000 BC the Sumerians might have been able to calculate monochord string-lengths which approximated 12edo to such a high degree of accuracy that their resulting tuning would be audibly indistinguishable from mathematically true 12edo.
Below is a tabulation of the cents values of 12-edo, arranged in descending scalar order:
12-edo degree cents 12 1200.0 11 1100.0 10 1000.0 9 900.0 8 800.0 7 700.0 6 600.0 5 500.0 4 400.0 3 300.0 2 200.0 1 100.0 0 0.0 (Note that by the definition of "cent", these cents values are exact.)
12-edo can be classified as a linear temperament, with the generator having an interval size of either a minor-2nd semitone (or its octave-complement a major-7th), or a perfect-5th (or its octave-complement a perfect-4th):
generator number of interval 12-edo degrees minor-2nd 1 perfect-4th 5 perfect-5th 7 major-7th 11
Because of the copious divisibility of its cardinality, using any other 12-edo intervals as generators will not produce the complete 12-edo tuning:
generator number of interval 12-edo degrees resulting scale major-2nd 2 6-edo (whole-tone scale) minor-3rd 3 4-edo (diminished-7th tetrad) major-3rd 4 3-edo (augmented triad) tritone 6 2-edo (tritone) minor-6th 8 3-edo (augmented triad) major-6th 9 4-edo (diminished-7th tetrad) minor-7th 10 6-edo (whole-tone scale)
(Therefore, the converse of this statement is that any EDO whose cardinality is a prime number, may use any of that EDO's intervals as a generator to generate the complete EDO.)
Concerning the various abbreviations: "12-eq" is the abbreviation formerly used by Monzo; it has been superceded in his work and that of many others by the adoption of "12-EDO" or "12-edo" generally, in cases where 12 equal divisions of the "octave" are considered to be a fundamental aspect of the tuning's musical usage, or by "12-ET or "12-tET" in the special (but frequent) circumstances where a temperament representing just-intonation is explicity intended.
After presenting some historical aspects, this webpage will examine 12-edo first as a tempering of pythagorean tuning, then as a meantone, and then finally as a member of some of the other families to which it belongs.
It is important to point out that standard musical staff notation is not based on 12-edo, which is a closed tuning resulting in a circle-of-5ths, but rather on open-ended chain-of-5ths types of tunings. From the earliest development of our modern musical theory and practice (that of the Franks c.800 AD), the notation was based on pythagorean tuning, in which the generator interval of the system is a "pure" perfect-5th with ratio 3:2 = 2,3-monzo [-1 1, > = ~701.955 cents, and sharps are a pythagorean-comma higher than their "enharmonically equivalent" flats.
Ab -- Eb -- Bb -- F --- C --- G --- D --- A --- E --- B --- F# -- C# -- G# -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 3-monzo 1086 588 90 792 294 996 498 0 702 204 906 408 1110 ~cents | | \|/ \|/ pythagorean-comma = ratio 531441/524288 = 2,3-monzo |-19 12, > = ~23.5 cents
Beginning around 1500, 1/4-comma meantone took over as the basis for the notation, in which the generator perfect-5th is now tempered narrower than "pure" and is expressed mathematically as (3/2)^((81/80)^(1/4)) = 2,3,5-monzo [0 0, 1/4 > = ~696.5784285 cents, making the flats a diesis higher than their "enharmonically equivalent" sharps.
Ab -- Eb -- Bb -- F --- C --- G --- D --- A --- E --- B --- F# -- C# -- G# -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 meantone 5th generator 1124 621 117 814 310 1007 503 0 697 193 890 386 1083 ~cents | | \|/ \|/ enharmonic diesis = ratio 128/125 = 2,3,5-monzo |7 0, -3 > = ~41 centsThroughout the "common-practice" period (c. 1600-1900), musical staff notation was adapted to the various varieties of the meantone family -- a process which only requires a pitch shift such that the flats are higher than the sharps; the notation itself remains unchanged from pythagorean, because as a chain-of-5ths tuning, meantones work exactly the same way as pythagorean.
As one tempers the 5th narrower than pythagorean "pure", the sharps get lower in pitch and the flats get higher, and as one tempers the 5th wider than 1/4-comma meantone, the flats get lower in pitch and the sharps get higher, and the pivot point in this process is 12-edo, where the sharps and flats are exactly equal in pitch to each other, making all those pairs of notes "enharmonically equivalent", as shown in the musical illustration at the top of this page.
There was an historical trend during the meantone era in Europe (c.1500-1850) of making the generator 5th wider, so that first 1/4-comma and 2/7-comma meantone were popular, then 1/5-comma, then finally 1/6-comma. Vincenzo Galilei proposed the use of 12-edo on lutes in 1581, the first mathematical description of it was published in China in 1584 by Zhu Zaiyu, and from the late 1600s various forms of 12-tone irregular circulating well-temperaments were devised and became widely used on keyboards. Beginning around 1800, Beethoven's use of frequent modulation to remote keys probably hastened listeners's acceptance of a 12-edo paradigm, and by the time of Wagner's death (1883) it had become nearly ubiquitous in Eurocentric music.
Below are some reasons that have been put forward as to why 12-edo become so widely accepted.
[Gene Ward Smith, Yahoo tuning group, message 58081 (Wed Apr 20, 2005 8:05 pm)]"My one-sentence answer is that 12 is the smallest number which gives usable major and minor triads."
[Joe Monzo, adapted from Yahoo tuning group, message 58084 (Wed Apr 20, 2005 9:23 pm)]"... In addition, 12 is the smallest number (cardinality, to be specific) which gives a reasonable representation of the patterns of L/s (in the form of tone and semitone) in the diatonic scales. For example, all diatonic major scales require approximately the pattern t:t:s:t:t:t:s. For the case where t=2s, the sum 5t+2s = 6t = 12s, which is 12-edo. ..."
[Neil Haverstick, Yahoo tuning group, message 58089 (Thu Apr 21, 2005 11:07 am)]"... Europeans were looking for a way to find a tuning system that would apply to music that modulated through a lot of chord changes, without sounding TOO much out of tune. ..."
In connection with Haverstick's comment, it is worth pointing out that beginning with Mozart, and continuing more strongly with Beethoven and Schubert, 12-edo's membership in the augmented temperament family began to be exploited more and more; the signpost of this technique is the use of pairs of enharmonically equivalent pairs of notes as common-tones -- in JI, the enharmonically equivalent pairs of notes are a diesis apart, ratio 128/125 = 2,3,5-monzo [7 0, -3> = ~41 cents; thus, in any tuning of the augmented family (among the others are 9, 15, 18, and 21-edo) the augmented-7th becomes the same pitch as the octave.
Then during later eras, Scriabin, Stravinsky, and other composers began exploiting 12-edo's membership in the diminished family with the use of the octatonic diminished scale. The unison-vector tempered out here is the "major diesis" of ratio 648/625 = 2,3,5-monzo [3, 4, -4 > = ~62.5 cents in JI; thus, in any tuning of the diminished family (among the others are 8, 16, 24, and 28-edo) the diminished-9th is the same pitch as the octave.
As composers sought new means of organizing musical pitches, the desire grew to explore these "new" temperament families and to modulate from one to another, a procedure which is facilitated by 12-edo's membership in so many different families. This process finally culminated in Schoenberg's idea of pantonality, and his acceptance of 12-edo as "12 tones which are related only with one another", first in the style now known as "free atonality" (1908-1913), and later (beginning 1917) in his serial method in which all pitches of the full 12-edo scale are circulated continuously in a composition.
Modern techniques of mass-production finally secured the place of 12-edo in the late 1900s, as millions of guitars and electronic keyboards were produced with 12-edo built in. Indeed, even the MIDI tuning specification and the vast majority of computer music software programs use 12-edo tuning as a basis, and in many cases alternative tunings are not available, or at the least are difficult to achieve and often require tedious editing.
12-edo arose historically by tempering out the pythagorean-comma. In a regular pythagorean chain of "pure" 5ths (each "5th" having the frequency ratio 3:2), the 12th note in the chain is nearly the same as the 7th "octave" above or below the starting note, differing by being wider by the pythagorean-comma of ~24 cents, a clearly perceptible difference.
Distributing this error (anomaly is really a better term here) among all 12 pitches -- by tempering the "5ths" to make each one ~2 cents narrower than the 3:2 ratio -- eliminates the pythagorean-comma (12 * -2 = -24 cents) and closes the cycle, so that the 12th note (in the chain of approximate 3:2s) has been narrowed by ~24 cents and is now exactly the same as the note which is 7 "octaves" above the starting note. The tempering of the 12edo "5th" is calculated thus:
2,3-monzo (prime-factor vector)
2 3 ratio cents
[-12/12 12/12> = 2-131 1.5 ~701.9550009 3:2 "pure 5th"
- [-19/12 12/12> = (2-19312)(1/12) ~1.001129891 ~1.955000865 1/12 pythagorean-comma
-----------------
[ 7/12 0 > ~1.498307077 700 12edo "5th"
(1/12 of Pythagorean comma is also called a grad.)
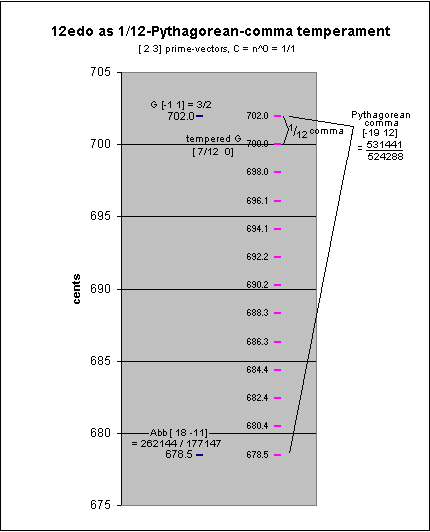
So the 12-EDO "5th", 2(7/12) = 7.00 Semitones = 700 cents, is ~1.955000865 cents narrower than the pythagorean (or just) "5th" of ratio 3:2. Expressed in fractions with increasing accuracy, this is 121/22, 164/67, or 185/89 cents narrow.
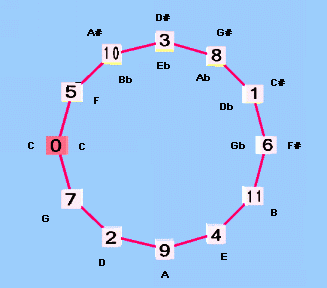
Below is a diagram showing the 12-edo "circle-of-5ths", with the 12-edo degree numbers in the cubes, and letter-name notation alongside, showing the closure of the system at Gb -6 = F# +6 generators (or Db -5 = C# +7, etc.):
Considering its low cardinality, 12-EDO gives a representation of 5-limit ratios which, while not very good, is decent enough that it has become accepted for use in representing 5-limit tunings and their derivitives. Thus, 12-EDO may also be considered as both a meantone and a schismic tuning.
As with all meantones, 12-EDO maps the "major 3rd" to +4 generators. The logarithmic pitch size of the syntonic comma is almost exactly 11/12 that of the pythagorean comma:
2,3,5-monzo
2 3 5 ratio ~cents
[-48/12 4, -1 > = (2-4345-1) syntonic comma 1.0125 21.5062896
- [209/12 11, 0 > 11/12 pythagorean comma 1.012499251 21.5050095
------------------
[161/12 -7, -1 > 1.000000739 0.001280077 (= ~1/781)
Because of this near-equivalence, 12-edo is nearly indistinguishable from 1/11-comma meantone. The 1/11-comma meantone "5th", or generator, is (3/2) / ((81/80)(1/11)) = ~ 699.9998836 cents:
2,3,5-monzo
2 3 5 ratio cents
[-11/11 11/11, 0/11 > = 2-131 1.5 ~701.9550009 3:2 "pure 5th"
- [ -4/11 4/11, -1/11 > = (2-4345-1)(1/11) ~1.001129958 ~1.955117236 1/11 syntonic-comma
--------------------------
[ -7/11 7/11, 1/11 > ~1.498306976 ~699.9998836 1/11-comma meantone "5th"
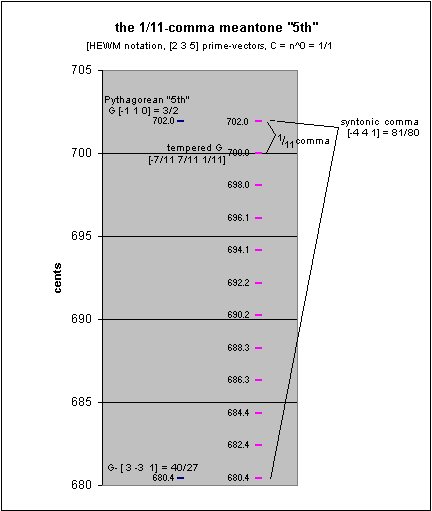
Interestingly, in 1/11-comma meantone, any two pitches which are separated by 12 generators are nearly identical, with only ~0.001396448 (~1/716) cent between them; here is a typical example:
for C = n0 = 1/1 :
2,3,5-monzo
2 3 5 ratio cents
[ 43/11 -21/11, -3/11> ~1.189207355 ~300.0003491 1/11-comma meantone -3 generator: Eb
- [-118/11 63/11, 9/11> ~1.189206396 ~299.9989527 1/11-comma meantone +9 generator: D#
--------------------------
[ 161/11 -84/11, -12/11> ~1.000000807 ~0.001396448 ~1/716 cent
Thus, it becomes in effect a closed 12-tone meantone, and is in every respect identical to 12-EDO. The difference between the two "5ths" is only ~1/8593 cent, really a negligible difference:
2,3,5-monzo
2 3 5 ratio cents
[ 77/132 0/11, 0/11> = [ 7/12 0 0 > ~1.498307077 700 12edo 5th"
- [-84/132 7/11, 1/11> = [-7/11 7/11, 1/11> ~1.498306976 ~699.9998836 1/11-comma meantone "5th"
------------------------
[161/132 -7/11, -1/11> ~1.000000067 ~0.000116371 difference between the two
As with all meantones, 12-edo represents the "major-3rd" (ratio 5:4) as 4 steps along the circle-of-5ths (i.e., +4 generator 5ths), which places its approximation of the major-3rd as 4 degrees of 12-edo (i.e., 4 semitones). Because 12 ÷ 4 = 3 with no remainder, the "circle-of-major-3rds" in 12-edo only contains 3 pitches and then cycles back onto itself again. Thus, when both the syntonic-comma and the diesis are used as unison-vectors, and the geometry of the 5-limit lattice is closed, to show an accurate representation of 12-edo's approximation of 5-limit just-intonation, the spiral which forms the circle-of-5ths connects the four separate triangles which form augmented triads. This can be plainly seen in the diagram below, adapted from a Tonescape® lattice, which shows the 12-edo 5-limit toroidal lattice.
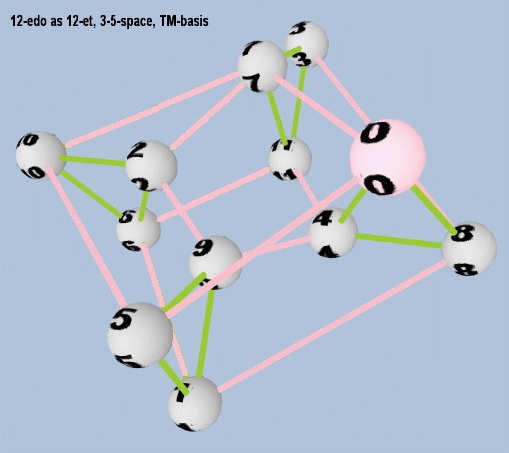
The major-3rds on this lattice have green connectors, so going counter-clockwise around the lattice, it can be seen that the four augmented triads are given in 12-edo by degrees 0-4-8, 1-5-9, 2-6-10, and 3-7-11. The magenta connectors show the circle-of-5ths which spirals around the torus to connect the augmented triads, as degrees 0-7-2-9-4-11-6-1-8-3-10-5-0 (as in the circle-of-5ths lattice shown above in the section describing 12-edo's pythagorean approximation).
12edo also functions as a schismic tuning, mapping the "major 3rd" to -8 generators. The grad -- the amount the 12edo "5th" is tempered narrow from the "pure" Pythagorean "5th" -- happens to be nearly equal to the skhisma:
2,3-monzo
2 3 ~cents
[ -19/12 1> 1.955000865 tempering of 12edo "5th" = grad
- [-180/12 8> = [-15, 8> 1.953720788 skhisma
---------------
[ 161/12 -7> 0.001280077 ~1/781-cent difference
(See Ellis's footnote * on p 316 of Helmholtz, On The Sensations Of Tone.)
Coincidentally, the amount of tempering of -8 generators (i.e., 8 "4ths" upward or 8 "5ths" downward) also happens to give the closest approximation to the "major 3rd" in 12edo, thus tempering out the skhisma.
Erv Wilson, in On the development of intonational systems by extended linear mapping (Xenharmonikôn 3, 1975), has noted that our familiarity with 12edo and its dual ability to map the "major 3rd", to both +4 and -8 generator "5ths", is advantageous in providing a path towards intonational expansion.:
The much maligned Cycle of 12 (and unjustly so) presents that unique coincidence of events whereby may be effected a remapping of the 5-function from the +4 linear position to the -8 linear position. And we may be in the process of doing that. It could not have happened in meantone. But the shift- ing from meantone, which allows only the +4 mapping of the 5-function, to the cycle of 12, which also allows the -8 mapping; this, combined with practice, in one major school, of avoiding 'diatonic patterns', that is, patterns where the +4 mapping has any effective meaning, suggests that remapping the 5-function to linear -8 is imminent. Likely it has already occured, and both orders of mapping are competing for dominance.
12edo is a very versatile tuning which belongs to yet other temperament families. Even in only the 5-limit, these include:
Below is a bingo-card lattice showing many of the different periodicity-blocks which may be formed by 12-edo in 3,5-primespace. The 3-axis runs horizontally from left to right, the 5-axis vertically from top to bottom, and since octave-equivalence is assumed, prime-factor 2 is ignored for the purposes of this diagram. In octave normalized form, prime-factor 3 is mapped to 7 degrees of 12-edo, and prime-factor 5 is mapped to 4 degrees.
In higher limits, 12edo belongs to the higher-limit versions of these families, as well as to other families.
During the 1800s, the use of 12edo became nearly universal in Euro-centric musical cultures, and as composers began to explore the incorporation of prime-factor 7 in their harmonies, 12edo was forced into service to represent ratios of 7. In 1911, Schoenberg published his Harmonielehre, in which he suggested that 12edo could be used to represent harmonies up to the 11-limit. Below is a graph which shows the error of 12edo in representing all ratios in the 11-odd-limit (i.e., those in Partch's tonality-diamond), as a percentage of one degree of 12edo.
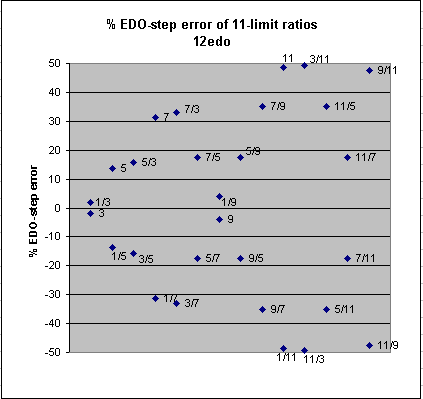
It can be seen that 12edo's success at representing the 11-limit ratios can be categorized as follows:
| excellent: | (1/3, 3/1), (1/9, 9/1) |
| mediocre: | (5/1, 1/5), (5/3, 3/5), (7/5, 5/7), (5/9, 9/5), (11/7, 7/11) |
| poor: | (7/1, 1/7), (7/3, 3/7), (7/9, 9/7), (11/5, 5/11) |
| terrible: | (11/1, 1/11), (3/11, 11/3), (9/11, 11/9) |
Below is a table showing how some of the most common 11-limit just-intonation ratios, and some others up to the 41-limit, are mapped to 12-edo, using the closest-fit mappings:
====================================
edomap.py (c)2008-12-23 by Joe Monzo
====================================
Finds the EDO mappings for a set of ratios
=============== new run =====================
please enter edo: 12
12 -edo floating-point mappings:
2 = 12.000000 +0.00 --> 12
3 = 19.019550 -0.02 --> 19
5 = 27.863137 +0.14 --> 28
7 = 33.688259 +0.31 --> 34
11 = 41.513179 +0.49 --> 42
13 = 44.405277 -0.41 --> 44
17 = 49.049554 -0.05 --> 49
19 = 50.975130 +0.02 --> 51
23 = 54.282743 -0.28 --> 54
29 = 58.295772 -0.30 --> 58
31 = 59.450356 -0.45 --> 59
37 = 62.513440 +0.49 --> 63
41 = 64.290624 -0.29 --> 64
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 12 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 19 = 1900.000000 cents <-- 1901.955001 - 2.0 cents
map 5 --> 28 = 2800.000000 cents <-- 2786.313714 +13.7 cents
map 7 --> 34 = 3400.000000 cents <-- 3368.825906 +31.2 cents
map 11 --> 42 = 4200.000000 cents <-- 4151.317942 +48.7 cents
map 13 --> 44 = 4400.000000 cents <-- 4440.527662 -40.5 cents
map 17 --> 49 = 4900.000000 cents <-- 4904.955410 - 5.0 cents
map 19 --> 51 = 5100.000000 cents <-- 5097.513016 + 2.5 cents
map 23 --> 54 = 5400.000000 cents <-- 5428.274347 -28.3 cents
map 29 --> 58 = 5800.000000 cents <-- 5829.577194 -29.6 cents
map 31 --> 59 = 5900.000000 cents <-- 5945.035572 -45.0 cents
map 37 --> 63 = 6300.000000 cents <-- 6251.344039 +48.7 cents
map 41 --> 64 = 6400.000000 cents <-- 6429.062406 -29.1 cents
--------------
examples:
ratio --> 12 -edo mapping:
ratio cents error edo cents name
2:1 = 1200.0 + 0.0 --> 12/12 = 1200.0 (octave)
31:16 = 1145.0 -45.0 --> 11/12 = 1100.0 (31st harmonic)
243:128 = 1109.8 - 9.8 --> 11/12 = 1100.0 (pythagorean major-7th)
15:8 = 1088.3 +11.7 --> 11/12 = 1100.0 (just major-7th, 5*3)
4096:2187 = 1086.3 +13.7 --> 11/12 = 1100.0 (pythagorean diminished-8ve)
13:7 = 1071.7 -71.7 --> 10/12 = 1000.0 (tridecimal superminor-7th)
11:6 = 1049.4 +50.6 --> 11/12 = 1100.0 (undecimal submajor-7th)
20:11 = 1035.0 -35.0 --> 10/12 = 1000.0 (undecimal superminor-7th)
29:16 = 1029.6 -29.6 --> 10/12 = 1000.0 (29th harmonic)
9:5 = 1017.6 -17.6 --> 10/12 = 1000.0 (just minor-7th)
16:9 = 996.1 + 3.9 --> 10/12 = 1000.0 (pythagorean minor-7th)
7:4 = 968.8 +31.2 --> 10/12 = 1000.0 (7th harmonic)
12:7 = 933.1 -33.1 --> 9/12 = 900.0 (septimal supermajor-6th)
27:16 = 905.9 - 5.9 --> 9/12 = 900.0 (pythagorean major-6th)
5:3 = 884.4 +15.6 --> 9/12 = 900.0 (just major-6th)
18:11 = 852.6 -52.6 --> 8/12 = 800.0 (undecimal neutral-6th)
13:8 = 840.5 -40.5 --> 8/12 = 800.0 (13th harmonic)
6561:4096 = 815.6 -15.6 --> 8/12 = 800.0 (pythagorean augmented-5th)
8:5 = 813.7 -13.7 --> 8/12 = 800.0 (just minor-6th)
128:81 = 792.2 + 7.8 --> 8/12 = 800.0 (pythagorean minor-6th)
11:7 = 782.5 +17.5 --> 8/12 = 800.0 (undecimal augmented-5th)
25:16 = 772.6 +27.4 --> 8/12 = 800.0 (just augmented-5th)
14:9 = 764.9 +35.1 --> 8/12 = 800.0 (septimal subminor-9th)
3:2 = 702.0 - 2.0 --> 7/12 = 700.0 (perfect-5th)
16:11 = 648.7 -48.7 --> 6/12 = 600.0 (11th subharmonic)
23:16 = 628.3 -28.3 --> 6/12 = 600.0 (23rd harmonic)
10:7 = 617.5 -17.5 --> 6/12 = 600.0 (septimal large-tritone)
729:512 = 611.7 -11.7 --> 6/12 = 600.0 (pythagorean augmented-4th)
1024:729 = 588.3 +11.7 --> 6/12 = 600.0 (pythagorean diminished-5th)
7:5 = 582.5 +17.5 --> 6/12 = 600.0 (septimal small-tritone)
11:8 = 551.3 +48.7 --> 6/12 = 600.0 (11th harmonic)
4:3 = 498.0 + 2.0 --> 5/12 = 500.0 (perfect-4th)
21:16 = 470.8 +29.2 --> 5/12 = 500.0 (septimal-4th, 7*3)
9:7 = 435.1 -35.1 --> 4/12 = 400.0 (septimal supermajor-3rd)
41:32 = 429.1 -29.1 --> 4/12 = 400.0 (41st harmonic)
14:11 = 417.5 -17.5 --> 4/12 = 400.0 (undecimal diminished-4th)
81:64 = 407.8 - 7.8 --> 4/12 = 400.0 (pythagorean major-3rd)
5:4 = 386.3 +13.7 --> 4/12 = 400.0 (just major-3rd)
8192:6561 = 384.4 +15.6 --> 4/12 = 400.0 (pythagorean diminished-4th)
11:9 = 347.4 +52.6 --> 4/12 = 400.0 (undecimal neutral-3rd)
39:32 = 342.5 -42.5 --> 3/12 = 300.0 (39th harmonic, 13*3)
19683:16384 = 317.6 -17.6 --> 3/12 = 300.0 (pythagorean augmented-2nd)
6:5 = 315.6 -15.6 --> 3/12 = 300.0 (just minor-3rd)
19:16 = 297.5 + 2.5 --> 3/12 = 300.0 (19th harmonic)
32:27 = 294.1 + 5.9 --> 3/12 = 300.0 (pythagorean minor-3rd)
7:6 = 266.9 +33.1 --> 3/12 = 300.0 (septimal subminor-7th)
37:32 = 251.3 +48.7 --> 3/12 = 300.0 (37th harmonic)
13:11 = 289.2 -89.2 --> 2/12 = 200.0 (tridecimal diminished-3rd)
8:7 = 231.2 -31.2 --> 2/12 = 200.0 (septimal tone)
9:8 = 203.9 - 3.9 --> 2/12 = 200.0 (pythagorean major-2nd/tone)
10:9 = 182.4 +17.6 --> 2/12 = 200.0 (just minor-tone)
11:10 = 165.0 +35.0 --> 2/12 = 200.0 (undecimal small-tone/submajor-2nd)
35:32 = 155.1 +44.9 --> 2/12 = 200.0 (35th harmonic, 7*5)
14:13 = 128.3 +71.7 --> 2/12 = 200.0 (tridecimal major-2nd)
12:11 = 150.6 -50.6 --> 1/12 = 100.0 (undecimal large-semitone)
13:12 = 138.6 -38.6 --> 1/12 = 100.0 (tridecimal minor-2nd)
14:13 = 128.3 +71.7 --> 2/12 = 200.0 (tridecimal major-2nd)
15:14 = 119.4 -19.4 --> 1/12 = 100.0 (septimal chromatic-semitone)
2187:2048 = 113.7 -13.7 --> 1/12 = 100.0 (pythagorean augmented-prime/apotome)
16:15 = 111.7 -11.7 --> 1/12 = 100.0 (just diatonic-semitone)
17:16 = 105.0 - 5.0 --> 1/12 = 100.0 (septendecimal semitone)
256:243 = 90.2 + 9.8 --> 1/12 = 100.0 (pythagorean minor-2nd/limma)
25:24 = 70.7 +29.3 --> 1/12 = 100.0 (just chromatic-semitone)
33:32 = 53.3 +46.7 --> 1/12 = 100.0 (33rd harmonic, 11*3)
1:1 = 0.0 + 0.0 --> 0/12 = 0.0 (prime)
some commas:
3-limit:
531441:524288 = 23.5 -23.5 --> 0/12 = 0.0 (pythagorean-comma)
5-limit:
648:625 = 62.6 -62.6 --> 0/12 = 0.0 (major-diesis)
250:243 = 49.2 +50.8 --> 1/12 = 100.0 (maximal-diesis)
128:125 = 41.1 -41.1 --> 0/12 = 0.0 (enharmonic-diesis)
34171875:33554432 = 31.6 +68.4 --> 1/12 = 100.0 (ampersand-comma)
3125:3072 = 29.6 +70.4 --> 1/12 = 100.0 (magic-comma)
81:80 = 21.5 -21.5 --> 0/12 = 0.0 (syntonic-comma)
2048:2025 = 19.6 -19.6 --> 0/12 = 0.0 (diaschisma)
2109375:2097152 = 10.1 +89.9 --> 1/12 = 100.0 (semicomma)
15625:15552 = 8.1 +91.9 --> 1/12 = 100.0 (kleisma)
32805:32768 = 2.0 - 2.0 --> 0/12 = 0.0 (skhisma)
7-limit:
36:35 = 48.8 -48.8 --> 0/12 = 0.0 (septimal-diesis)
49:48 = 35.7 +64.3 --> 1/12 = 100.0 (septimal-comma-3 - 7/6 : 8/7)
50:49 = 35.0 -35.0 --> 0/12 = 0.0 (septimal-comma-2)
64:63 = 27.3 -27.3 --> 0/12 = 0.0 (septimal-comma)
225:224 = 7.7 - 7.7 --> 0/12 = 0.0 (septimal-kleisma)
11-limit:
22:21 = 80.5 +19.5 --> 1/12 = 100.0 ()
33:32 = 53.3 +46.7 --> 1/12 = 100.0 (undecimal-diesis)
45:44 = 38.9 -38.9 --> 0/12 = 0.0 ()
55:54 = 31.8 +68.2 --> 1/12 = 100.0 ()
56:55 = 31.2 -31.2 --> 0/12 = 0.0 ()
121:120 = 14.4 +85.6 --> 1/12 = 100.0 (11/10 : 12/11 comma)
| 12=0 | 2:1 = 1:1 |
| 11 | 15:8 , 17:9 , 168:89 , 185:98 |
| 10 | 7:4 , 9:5 , 16:9 , 41:23 , 57:32 , 98:55 |
| 9 | 5:3 , 37:22 |
| 8 | 8:5 , 19:12 , 27:17 , 100:63 , 227:143 |
| 7 | 3:2 , 442:295 |
| 6 | 7:5 , 17:12 , 41:29 , 99:70 , 239:169 |
| 5 | 4:3 , 295:221 |
| 4 | 5:4 , 29:23 , 34:27 , 63:50 , 286:227 , 349:277 |
| 3 | 6:5 , 19:16 , 25:21 , 44:37 |
| 2 | 9:8 , 55:49 |
| 1 | 16:15 , 17:16 , 18:17 , 89:84 , 196:185 |
| 0 | 1:1 |
| progressing to the right = greater accuracy of approximation and greater complexity | |
[Joe Monzo]
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.