In 1482, Bartolomeo Ramos (sometimes spelled Ramis) published
the first description of the procedure to divide a
monochord string
so as to produce 5-limit
ratios.
Ever since Boethius had written his treatise on music c. 505 AD, for almost 1000 years European musicians and theorists had assumed that the diatonic scale should be tuned to 3-limit "pythagorean" ratios. Boethius knew that he was witnessing the disintegration of the Western Roman Empire, and engaged himself in the project of translating great Greek classics into Latin because he knew that soon no-one in the west would be able to understand Greek.
Boethius discussed many of the subtle aspects of tuning that had been written about in Greek books, and gave monochord measurements for all three of the basic Greek genera: diatonic, chromatic, and enharmonic. But due to the illiteracy of the ensuing centuries, his readers failed to understand the less familiar chromatic and enharmonic, and so the diatonic, in Boethius's Pythagoran tuning, became firmly established as "the" scale in the treatises written from c.800 until about 1300.
(In practice, there were most likely purely musical reasons for the limitation to the diatonic scale, if indeed the musical practice of the time was so limited, but unfortunately the theory treatises are the only source of information we have on tuning during this period.)
During the 1100s and 1200s, soldiers returning to Europe after the Crusades brought back with them many manuscripts containing ancient Greek music-theory treatises. As theorists began to learn Greek and understand what these books contained, the desire grew for contemporary use of those musical resources, particularly the tunings which produced intervals which were both smaller and more consonant than those of the Pythagorean scale.
Some theorists of the early 1300s, notably Walter Odington and Marchetto of Padua, wrote about singers using intonation different from the Pythagorean tuning. Odington specifically states that singers substitute 5-limit ratios for Pythagorean ones, while Marchetto's interesting advocacy of "1/5-tones" is open to interpretation (as can be seen in my webpage about his work).
At some point during the 1400s it became fairly common for keyboards to tuned be to a variant of regular Pythagorean tuning, employing the skhismic major-3rd, such that the note whose ratio is prime-factored as 3-8 represents the JI "major-3rd" whose ratio is 5:4 (e.g., if "C" is the 1:1, "Fb" represents "E"), the difference between those two being only the ~2-cent schisma, which is below the threshold of typical human error in manual tuning. This is thus known as "schismatic tuning".
Ramos's work of 1482 is the first mathematical description of 5-limit tuning in Europe since the work of Ptolemy of c. 150 AD. After a few decades of debate, 5-limit JI rapidly became the established tuning, at least in theory. In practice, by 1529 Pietro Aron was already describing temperament, in the form of 1/4-comma meantone, but even here the objective was to preserve the consonance of the 5-limit ratios.
from the musica practica of Bartolomeo Ramos (1482)
(English translation from Oliver Strunk, Source Readings in Music History)
Part One - 1st Treatise
2. THE DIVISION OR COMPOSITION OF THE REGULAR MONOCHORD
The regular monochord has been subtly divided by Boethius with
numbers and measure. But although this division is useful and pleasant
to theorists, to singers it is laborious and difficult to understand. And
since we have promised to satisfy both, we shall give a most easy division
of the regular monochord. Let no one think that we have found this with
ordinary labor, we who have indeed discovered it reading the precepts
of the ancients in many vigils and avoiding the errors of the moderns
with care. And anyone even moderately informed will be able to understand it.
Let there be a string or chord of any length, and let this be
stretched over a piece of wood having a certain concavity, and let the
end to which the string is bound be marked at the point a. And let the
end to which the string is drawn and stretched, placed in a straight line
and at a distance, be marked at the point q.
Now let the quantity aq, that is, the length of the whole string, be divided into two equal parts,
and let the point of equal distance be marked with the letter h.
The quantity
ha we again divide in half, and in the middle of the division we put
the letter d.
The quantity hd is again bisected, and in the middle of the
section the letter f is set down.
Understand the same to be done also with the other half of the string,
that is, with hq, for in the first division the letter p will
be inscribed at the midpoint,
and in the division hp the letter l will be put
equidistant from either end,
and between l and p, when the same rule of intervals
has been observed, we shall introduce the letter n.
And when we divide fn by half we inscribe the letter i.
But we shall not go on to smaller parts by means of this division by
half until we have made other divisions. Thus we divide the whole,
aq, by three, and measuring from q, we put the letter
m at the end of one third and the letter e at the end
of two thirds.
Then let eq be again divided by three, and going from q toward
e, let the sign ♮ quadrum be set down
at two thirds
and, when the quantity ♮ quadrum to q has been doubled,
let the letter b be inscribed.
Now we again bisect the quantity mh, and we mark the middle of
the section with the letter k.
And when we double the quantity kq, we put
the letter c at the end of the duplication.
Now between e and ♮ quadrum
let the letter g stand equidistant from either end.
Then when we divide gq into two equal parts, we inscribe the
letter o.
Thus the whole monochord has been divided by a legitimate partition,
as you will see in the diagram below.
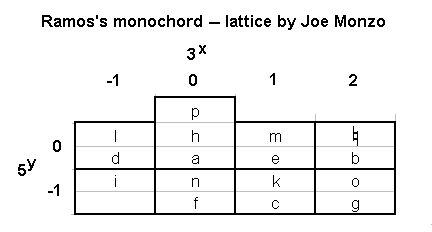
The tuning described above by Ramos may be shown on a
lattice diagram
drawn in [3,5]-primespace
(i.e., ignoring
prime-factor
2, which represents the separation of any pair of Ramos's pitches
by an 8ve), thus:
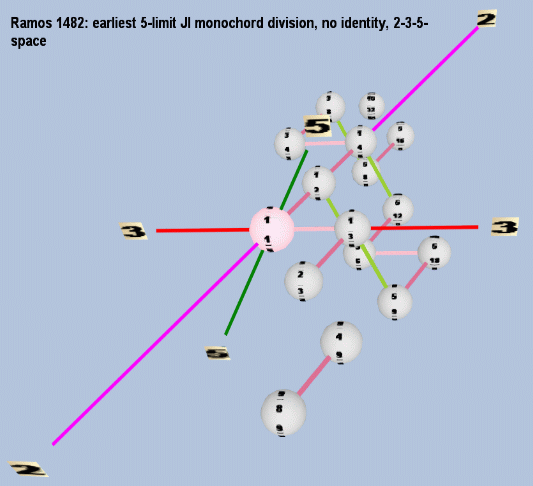
Below is a version of the same lattice using triangular geometry, created with Tonescape®.
Ramos's entire monochord scale is illustrated below in regular
musical staff notation, using HEWM
"plus sign" accidentals to
indicate the presence of prime-factor 5 in the appropriate notes:
Note that the note-functions of Ramos's monochords follow exactly the pattern of the ancient Greek Perfect Immutable System (PIS).
see also
Ramos's tuning
as a periodicity-block
Updated: