For a ratio a/b, the logarithm of a*b. It is a measure of harmonic complexity developed by James Tenney.
This distance function is a special use of the Minkowski metric in a tonal space where the units along each of the axes are the logarithms of prime numbers.
[For example], the harmonic distance of the interval 7:9 is 2*log(3)+log(7).
I wonder why, in this definition, Chalmers refers to the city-block metric as the "Minkowski metric". The only definitions of the Minkowski metric I've ever seen are:
the usual special relativistic space-time distance -- see:
and a generalized Euclidean metric where the exponents 2 and 1/2 are replaced with p and 1/p respectively (p can be infinite, in which case one takes a limit):
So what Chalmers really means is, using the second definition, the Minkowski first-order metric. Subject to Chalmers' approval, I suggest we change that definition.
It also might help to give an example using a ratio with one even number, to emphasize that one doesn't ignore factors of 2 in this computation.
Go ahead and clarify the definition of city-block, aka Taxicab, aka Manhattan, aka Minkowski metric.
For the set of prime-factors p1, p2, ... pn having associated exponents e1, e2, ... en , the log(2) Tenney harmonic-distance is calculated as: (ABS(e1)*[LOG(p1)*(1/LOG(2))]) + (ABS(e2)*[LOG(p2)*(1/LOG(2))]) + ...
Below is a table of the log(2) harmonic-distance for some intervals in the 11-limit, ranked in ascending order of harmonic-distance.
2,3,5,7,11-monzo ratio ~cents Tenney HD [ 1 0, 0 0 0 > 2 / 1 1200 1.0 [ -1 1, 0 0 0 > 3 / 2 701.9550009 2.584962501 [ 2 -1, 0 0 0 > 4 / 3 498.0449991 3.584962501 [ 0 -1, 1 0 0 > 5 / 3 884.358713 3.906890596 [ -2 0, 1 0 0 > 5 / 4 386.3137139 4.321928095 [ -2 0, 0 1 0 > 7 / 4 968.8259065 4.807354922 [ 1 1, -1 0 0 > 6 / 5 315.641287 4.906890596 [ 0 0, -1 1 0 > 7 / 5 582.5121926 5.129283017 [ 3 0, -1 0 0 > 8 / 5 813.6862861 5.321928095 [ -1 -1, 0 1 0 > 7 / 6 266.8709056 5.392317423 [ 0 2, -1 0 0 > 9 / 5 1017.596288 5.491853096 [ 3 0, 0 -1 0 > 8 / 7 231.1740935 5.807354922 [ 0 2, 0 -1 0 > 9 / 7 435.0840953 5.977279923 [ -1 -1, 0 0 1 > 11 / 6 1049.362941 6.044394119 [ 1 0, 1 -1 0 > 10 / 7 617.4878074 6.129283017 [ -3 2, 0 0 0 > 9 / 8 203.9100017 6.169925001 [ 0 0, 0 -1 1 > 11 / 7 782.4920359 6.266786541 [ 2 1, 0 -1 0 > 12 / 7 933.1290944 6.392317423 [ -3 0, 0 0 1 > 11 / 8 551.3179424 6.459431619 [ 1 -2, 1 0 0 > 10 / 9 182.4037121 6.491853096 [ 0 -2, 0 0 1 > 11 / 9 347.4079406 6.62935662 [ -1 0, -1 0 1 > 11 / 10 165.0042285 6.781359714 [ -3 1, 1 0 0 > 15 / 8 1088.268715 6.906890596 [ 1 -2, 0 1 0 > 14 / 9 764.9159047 6.977279923 [ 2 1, 0 0 -1 > 12 / 11 150.6370585 7.044394119 [ 4 -2, 0 0 0 > 16 / 9 996.0899983 7.169925001 [ 1 0, 0 1 -1 > 14 / 11 417.5079641 7.266786541 [ 0 1, 1 0 -1 > 15 / 11 536.9507724 7.366322214 [ 4 0, 0 0 -1 > 16 / 11 648.6820576 7.459431619 [ 1 2, 0 0 -1 > 18 / 11 852.5920594 7.62935662 [ 2 0, 1 0 -1 > 20 / 11 1034.995772 7.781359714 [ 4 -1, -1 0 0 > 16 / 15 111.7312853 7.906890596 [ -4 0, 2 0 0 > 25 / 16 772.6274277 8.64385619 [ -4 3, 0 0 0 > 27 / 16 905.8650026 8.754887502 [ -1 -2, 2 0 0 > 25 / 18 568.717426 8.813781191 [ -2 3, -1 0 0 > 27 / 20 519.5512887 9.076815597 [ -3 -1, 2 0 0 > 25 / 24 70.67242686 9.22881869 [ 0 3, -2 0 0 > 27 / 25 133.2375749 9.398743692 [ 5 0, -2 0 0 > 32 / 25 427.3725723 9.64385619 [ 5 -3, 0 0 0 > 32 / 27 294.1349974 9.754887502 [ 2 2, -2 0 0 > 36 / 25 631.282574 9.813781191 [ 3 -3, 1 0 0 > 40 / 27 680.4487113 10.0768156 [ 4 1, -2 0 0 > 48 / 25 1129.327573 10.22881869 [ 1 -3, 2 0 0 > 50 / 27 1066.762425 10.39874369 [ -5 2, 1 0 0 > 45 / 32 590.2237156 10.4918531 [ 6 -2, -1 0 0 > 64 / 45 609.7762844 11.4918531 [ -1 4, -2 0 0 > 81 / 50 835.1925757 11.98370619 [ -6 1, 2 0 0 > 75 / 64 274.5824286 12.22881869 [ -6 4, 0 0 0 > 81 / 64 407.8200035 12.33985 [ -4 4, -1 0 0 > 81 / 80 21.5062896 12.6617781 [ 2 -4, 2 0 0 > 100 / 81 364.8074243 12.98370619 [ 7 -1, -2 0 0 > 128 / 75 925.4175714 13.22881869 [ 7 -4, 0 0 0 > 128 / 81 792.1799965 13.33985 [ 5 -4, 1 0 0 > 160 / 81 1178.49371 13.6617781 [ 7 0, -3 0 0 > 128 / 125 41.05885841 13.96578428 [ -7 3, 1 0 0 > 135 / 128 92.17871646 14.0768156 [ -7 2, 2 0 0 > 225 / 128 976.5374295 14.81378119 [ -7 5, 0 0 0 > 243 / 128 1109.775004 14.9248125 [ 8 -3, -1 0 0 > 256 / 135 1107.821284 15.0768156 [ -5 5, -1 0 0 > 243 / 160 723.4612905 15.2467406 [ 8 -2, -2 0 0 > 256 / 225 223.4625705 15.81378119 [ 8 -5, 0 0 0 > 256 / 243 90.22499567 15.9248125 [ 6 -5, 1 0 0 > 320 / 243 476.5387095 16.2467406 [ -8 4, 1 0 0 > 405 / 256 794.1337173 16.6617781 [ 9 -4, -1 0 0 > 512 / 405 405.8662827 17.6617781 [ -9 3, 2 0 0 > 675 / 512 478.4924303 18.39874369 [ -9 6, 0 0 0 > 729 / 512 611.7300052 18.509775 [ -7 6, -1 0 0 > 729 / 640 225.4162913 18.8317031 [ 10 -3, -2 0 0 > 1024 / 675 721.5075697 19.39874369 [ 10 -6, 0 0 0 > 1024 / 729 588.2699948 19.509775 [ 8 -6, 1 0 0 > 1280 / 729 974.5837087 19.8317031 [-10 5, 1 0 0 > 1215 / 1024 296.0887182 20.2467406 [-10 4, 2 0 0 > 2025 / 1024 1180.447431 20.98370619 [ 11 -5, -1 0 0 > 2048 / 1215 903.9112818 21.2467406 [ -8 7, -1 0 0 > 2187 / 1280 927.3712922 21.4166656 [ 11 -4, -2 0 0 > 2048 / 2025 19.55256881 21.98370619 [-11 7, 0 0 0 > 2187 / 2048 113.6850061 22.09473751 [ 9 -7, 1 0 0 > 2560 / 2187 272.6287078 22.4166656 [-11 6, 1 0 0 > 3645 / 2048 998.0437191 22.8317031 [ 12 -7, 0 0 0 > 4096 / 2187 1086.314994 23.09473751 [ 12 -6, -1 0 0 > 4096 / 3645 201.9562809 23.8317031 [-12 8, 0 0 0 > 6561 / 4096 815.6400069 24.67970001 [-10 8, -1 0 0 > 6561 / 5120 429.3262931 25.0016281 [ 13 -8, 0 0 0 > 8192 / 6561 384.3599931 25.67970001 [ 11 -8, 1 0 0 > 10240 / 6561 770.6737069 26.0016281 [-13 7, 1 0 0 > 10935 / 8192 499.9987199 26.4166656 [ 14 -7, -1 0 0 > 16384 / 10935 700.0012801 27.4166656 [-14 9, 0 0 0 > 19683 / 16384 317.5950078 28.26466251 [-15 8, 1 0 0 > 32805 / 32768 1.9537208 30.0016281 [-15 10, 0 0 0 > 59049 / 32768 1019.550009 30.84962501 [ 16 -8, -1 0 0 > 65536 / 32805 1198.046279 31.0016281 [-17 11, 0 0 0 > 177147 / 131072 521.5050095 34.43458751 [-19 12, 0 0 0 > 531441 / 524288 23.46001038 38.01955001
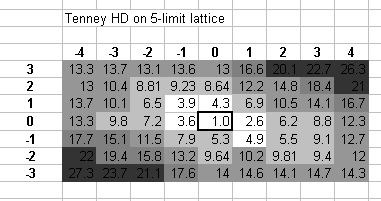
Below is a 2-dimensional lattice showing the log(2) harmonic-distance of some 5-limit ratios. Shades of grey represent 5-unit ranges of harmonic-distance thus:
0 - 5 white 5 - 10 lightest grey 10 - 15 medium-light grey 15 - 20 medium-dark grey 20 - 25 darkest grey
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.