diesis (διησισ)
(Greek: "sending thru", plural: dieseis)
Semitone or microtone, any interval less than about one third of the Fourth [i.e., <166 cents], usually refers to intervals of 1/2, 3/8, 1/3, or 1/4 of a tone of 200 ¢. [Thus: 100, 75, 662/3, and 50 cents.]
Diesis is a term which has been used so variously at different times in history that it requires 7 separate definitions here.
When the term is unqualified, it generally is meant to refer to the ratio 128:125 (2,3,5-monzo [ 7 0, -3 > ) = ~41.05885841 (~41 1/17) cents, the "enharmonic diesis", as described in definition #4 below.
1. minor semitone - earliest usage, by Philolaus
The historically prior usage of this term is by Philolaus (fl. c. 400 BC), as quoted by Boethius, to refer to the interval that is normally known as a limma (or Pythagorean "minor semitone" or diatonic semitone), with the ratio 256:243 (= 2,3,5-monzo [ 8 -5, 0 > ) = ~90.22499567 cents.
2. quarter-tones, by Aristoxenus
A variety of intervals smaller than the limma were called diesis in ancient Greek theory, including the so-called 'quarter-tones' of Aristoxenus. The term was revived in medieval Europe when the ancient Greek treatises became known and were translated into Latin. There was no one specific measurement, but the values clustered approximately around 50 cents.
3. 1/5-tones, by Marchetto
The infamous "fifth-tones" of Marchetto of Padua were named by him "dieses". According to Joseph Monzo's analysis, Marchetto's dieses were of five different sizes: approximately 22, 44, 45, 46, and 47 cents.
The group of the four larger ones are best viewed as variants of one generic size, so that it may be said that Monzo's interpretation of Marchetto's dieses posits two basic sizes, ~22 cents and ~44...47 cents.
This usage has a modern counterpart in the 31-edo [or 31-ET] system, in which the (slightly-smaller-than-)"fifth-tone" was named "diesis" by Fokker. This interval is 2(1/31) [= 0.39 Semitone = ~38.70967742 cents]. The formula for calculating this 31-edo-diesis-value of any ratio r is: dieses = log10(r) * [31 / log10(2)] or dieses = log2(r) * 31.
31-edo-dieses calculator
4. several specific 5-limit intervals
The term "diesis" is also used with a qualifying adjective to designate several specific 5-limit just intonation intervals.
Taken together, Rameau and Ellis named 3 dieses, but not in a consistent manner. The two named by Rameau were called "major diesis" and "minor diesis". Ellis confusingly called Rameau's "minor diesis" by the name "great diesis", and chose another interval altogether as his "small diesis".
Ellis's chart [see p 453 of his translation of Helmholtz, On the Sensations of Tone] defined these two dieses:
- small diesis, with a ratio of 3072:3125 (= 2,3,5-monzo [ -10 -1, 5 > ) = 0.29 Semitone = ~29.61356846 cents (today usually called the "magic comma");
- great diesis, with a ratio of 125:128 (= 2,3,5-monzo [ 7 0, -3 > ) = 0.41 Semitone = ~41.05885841 cents (today usually called "enharmonic diesis" or just plain "diesis" -- when it vanishes, differently-spelled notes are considered to be "enharmonically equivalent").
Rameau defined these two dieses:
- minor diesis, with ratio 125:128 (same as Ellis "great diesis");
- major diesis with a ratio of 243:250 (= 2,3,5-monzo [ 1 -5, 3 > ) = 0.49 Semitone = ~49.16613727 cents (today usually called "maximal diesis").
Monzo, 5-limit intervals, 100 cents and under suggests calling these, respectively, the "super-pentapental", "sub-tripental", and "super-tripental diesis". These names describe precisely the power of prime-factor 5 for each of these ratios.
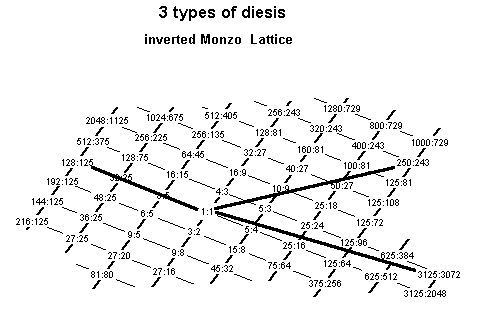
Below is a Monzo lattice in 3,5-prime-space illustrating the prime-factorization of these three types of dieses:
Below is a Tonescape® lattice in 3,5-prime-space, labeled with regular letter notation using "A" as the reference, with a blue arrow illustrating the enharmonic-diesis (Ellis's "great diesis"):
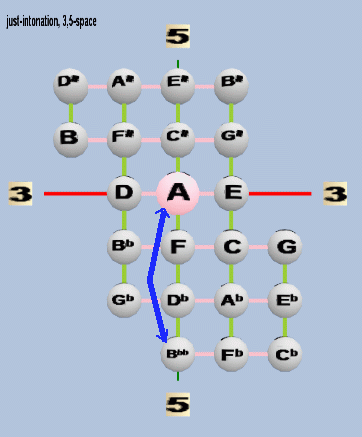
When this particular diesis is tempered-out, it results in a temperament which belongs to the "augmented" (or "diesic") temperament family. A good example is the familiar 12-edo, in which "A" and Bbb" are the same pitch, and so are all other pairs of notes on this lattice which would be connected by the same blue arrow: E:Fb, F#:Gb, C#:Db, G#:Ab, A#:Bb, E#:F, and B#:C. Some other EDOs which temper-out the enharmonic-diesis, and thus also belong to the augmented family, are 15-edo and 18-edo.
12-edo also has other enharmonically-equivalent pairs which appear on this lattice, such as B:Cb and D#:Eb -- these two pairs are examples of another interval called "major-diesis", which has the ratio 648:625, and whose tempering-out forms temperaments of the diminished family, shown with a blue arrow on this diagram:
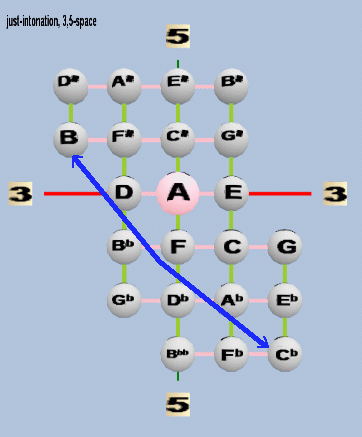
5. various intervals in the range of 40 - 70 cents
Joe Monzo uses the term "diesis" with a qualifier, to indicate any interval of approximately 40 to 70 cents.
For example, the "undecimal diesis" has the ratio 33:32 and is ~53.27294323 cents, and indicates the intonational difference represented by the accidental ^ in Monzo's use of 72-edo to accompany the JustMusic Prime-Factor Notation (AKA "HEWM notation) in notating the pitches F : F^.
Another example of a commonly-encountered ratio in this range is the "septimal" diesis, ratio 36:35 = ~48.7703814 cents. The intonational difference indicated by this diesis may be notated in HEWM with either the simplified 72-edo form, which is the same ^ as above, or in the more complicated JI form, by the combination >+ which follows the ratios strictly.
6. The "quomma" of miracle tunings
The "s" (= smaller of the two step-sizes) in the blackjack scale is another type of diesis, called the "quomma". In the typical 72-edo tuning of blackjack, this interval is 2(2/72) = 331/3 cents.
7. 19-edo diminished-2nd
One important tempered incidence of the "enharmonic diesis" which is somewhat different in size from most others, is that of 19-edo and 1/3-comma meantone (which are essentially the same tuning), in which it functions intervalically as the "diminished-2nd" (exactly as in 31-edo as described above in #3), and in which it is, respectively, one degree of 19edo = 2(1/19) = ~63.15789474 cents, and the ratio 625:648 (= 2,3,5-monzo [ -3 -4, 4 > ) = ~62.565148 cents in 1/3-comma meantone.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
