Paper for the conference of the Center François Viète
Problems of translation in the 18th century
Nantes, January 17, 1997
In RED, translation from Latin by Monzo. My translations are more
literal than Prof. Bailhache's; they have been retained where there
may be a subtle difference in meaning.
In GREEN, Monzo's English version of Prof. Bailhache's French
translation of Euler's Latin (contributed specifically
for this translation).
In MAGENTA (at the end), the translator's notes, and
observations from others.
By the middle of the 1700s, at the time when the music known as classical acquires its letters of nobility with Bach (1685-1750), Handel (1685-1759), Rameau (1683-1764), Haydn (1732-1809), Mozart (1756-1791), etc., two particularly famous mathematicians, Euler and d'Alembert, produce theories of music. This fact is obviously not the result of a "historical chance". It represents on the contrary the prolongation of one tradition.1 By the end of the previous century, several scientists had already become intrigued and put their attention on the same subject: Descartes (Compendium musicae), Galileo (end of the 1st day of Discorsi), Mersenne (the enormous work of the Universal Harmony), Leibniz "as an amateur".2 But in the 1700s, it is the music itself which changes, the traditional harmony dethroning the medieval counterpoint definitively. Thus this change had to be explained, to make the theory of it, and the task could inspire, rightly, any scientist set on music.
Euler (1707-1783) is 24 years old when he writes, in 1731, his Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae (A attempt at a new theory of music, exposed in all clearness according to the most well-founded principles of harmony). It is a work of 263 pages, written in Latin, which will be published only in 1739. It was translated into French one century later with the edition of Brussels of works of the mathematician. I will presently say some words on the quality of this translation.
In 1739 Euler is already known as a mathematician and is in St Petersburg, where he will soon occupy the Chair of mathematics. He is extremely interested by all that touches on music. He published in Basle, in 1727, a "thesis on sound" where he compares the sounds produced by the vibrating cords with those generated by the wind instruments. And about 1726 already, Euler had projected the plan of a considerable work on music. Apart from the fact that the sounds were to be noted there by sequence numbers in the scale, the object of study remained close to musical realities. The last section, for example, was to analyze the various kinds of pieces of music (saraband, courrant, etc). But the departure of the mathematician for St Petersburg (1727) and his other work prevented him from proceeding in this initial way. It is finally a much more mature work which was born in 1739.3
Euler remained all the rest of his life interested by the questions of music. He brought precise details to his new theory with some articles4 showing, as we will see, that he could take account of criticisms which one had addressed to his conceptions.5 Plus, I even believe and I will try to show it that he gave up one of the fundamental assumptions of his theory, without acknowledging it expressly.
Passing on the first chapter (on sound and hearing), I come immediately to the bases of Euler's musical theory (he talks in the second chapter "de suavitate et principiis harmoniae"). How to explain that certain sounds appear pleasant and others not? It seems paradoxical to find a rule, since everyone does not like the same things, or the taste of the same person can evolve. Can one lock up an art, like music, in laws? Euler answers that, as for all the fine arts, it is necessary to trust the opinion of enlightened people, therefore in music those whose ear was exerted and who will be able to see the right laws which dictates nature:
"Sed Musicum similem se genere oportet Architecto, qui plurimorum perversa de aedificiis iudicia non curans secundum certas et in natura ipsa fundatas leges aedes exstruit; quae etiamsi harum rerum ignaris non placeant, tamen, dum intelligentibus probentur, contentus est." [OO, 3a, I, 224]
["We will answer that the musician must act like the architect who, worrying little about the bad judgements which the ignorant multitudes pass on the buildings , builds according to unquestionable laws based on nature, and is satisfied with the approval of the people who are enightened in this matter."
]
- Bailhache/Monzo
This preliminary remark being made, Euler affirms that any pleasure comes from the perception of the perfection, any normally-constituted person seeking this:
"Certum est enim perceptionem perfectionis voluptatem parere hocque omnium spirituum esse proprium, ut perfectionibus detegendis et intuendis delectentur, ea vero omnia, in quibus vel perfectionem deficere vel imperfectionem adesse intelligunt, aversentur." [OO, 3a, I, 225]
["It is certain that any perception of perfection gives birth to pleasure and that it is a property common to every spirit, as much to delight itself with the discovery and contemplation of a perfect object, as to avoid what misses perfection or exposes its imperfections." - Bailhache/Monzo
]
However, as the example of a clock shows us, perfection is reduced to order.
"Contemplemur exempli causa horologium, cuius finis est temporis partes et divisiones ostendere: id maxime nobis placebit, si ex eius structura intelligimus omnes eius partes ita esse confectas et inter se conjunctas, ut omnes ad tempus exacte indicandum concurrant."
["'Let us contemplate as an example the mechanism of a clock, whose goal is to show the parts and divisions of time: it gives us maximum pleasure, if out of that structure we comprehend how all the parts are intertwined with each other, and how their actions all converge to indicate the exact time.
"Ex hisce sequitur, in qua re insit perfectio, in eadem ordinem necessario inesse debere." [OO, 3a, I, 225]
From this it follows, in that which incorporates perfection, likewise to order must it necessarily be indebted" - Monzo] T2[Let us take for example a clock, whose destination is to mark divisions of time; we will like it with the highest degree, if the examination of the structure makes us understand that the various parts are laid out and combined by it in such a way that all contribute to indicate time with exactitude.
Thus, in any thing where there is perfection, there is necessarily also order. - Bailhache]
"Vicissim igitur etiam intelligitur, ubi sit ordo, ibi etiam esse perfectionem et legem regulamve ordinis respondere scopo perfectionem efficienti." [OO, 3a, I, 226]
[Reciprocally, one can say that where there is order, there is perfection, and that the rule or law of the order corresponds to the goal which marks the perfection. - Bailhache/Monzo]
This notion of order is the key to the theory. However, it still remains to adapt it to the field of music. The order of things can be perceived in two ways: either one knows already the rules and one recognizes the presence of it immediately; or the rules are unknown, and one must then seek them, to reveal them (detego); music conforms to this second process:
"Duobus autem modis ordinem percipere possumus; altero, quo lex vel regula nobis iam est cognita, et ad eam rem propositam examinamus; altero, quo legem ante nescimus atque ex ipsa partium rei dispositione inquirimus, quaenam ea sit lex, quae istam structuram produxerit. Exemplum horologii supra allatum ad modum priorem pertinet; iam enim est cognitus scopus seu lex partium dispositionis, quae est temporis indicatio; ideoque horologium examinantes dispicere debemus, an structura talis sit, qualem scopus requirit. Sed si numerorum seriem aliquam ut hanc 1, 2, 3, 5, 8, 13, 21 etc. ascipio nescius, quae eorum progressionis sit lex, tum paullatim eos numeros inter se conferens deprehendo quemlibet esse duorum antecedentium summam hancque esse legem eorum ordinis affirmo."
"Posterior modus percipiendi ordinis ad musicam praecipue spectat" [OO, 3a, I, 226]["There are two ways in which we are able to perceive order; the one, in which the law or rule is already known to us, and to that matter being proposed, we simply examine; the other, in which the law before we were ignorant and out of the regular arrangement of parts we inquire, so that that we may construct laws. The example of the clock given above belongs to the first sort; one already knows the goal or law of the regular arrangement of the parts, which is the indication of a time value; thus on examining a clock we only need to discern, whether its structure is such, as this goal demands. But if the number series somehow were this 1, 2, 3, 5, 8, 13, 21 etc. and we had to consider unaware, what is the law of their progression, then gradually the comparison of those numbers among themselves will allow anyone to discover that each is the sum of the two previous and consequently thus is the law of their order confirmed.
The second manner of recognizing order is present especially in music." - Monzo]We can recognize order in two manners. When the law which is the reason is known to us, it is sufficient to examine whether the object under consideration satisfies it. But if we lack this data, it is necessary to seek to discover, in the organization of the parts of the object, the law which governs their arrangement; the recognized law, the order, will be the consequence. The clock quoted previously offers an example of the first case: the goal or the law of the provision of the parts is known there, it is the indication of time. Thus, when we examine a clock, we have only to check if its construction answers this goal. But if we have to consider, for example, the series of numbers 1, 2, 3, 5, 8, 13, 21, etc, without knowing which is the law of their increase, the comparison of these numbers makes us soon discover that each one is the sum of both which precede it; we consequently know the law of formation of the series, i.e., we know the order which reigns there.
The second manner of recognizing order is present especially in music." - Bailhache]
It remains to determine of what consists the order of sounds. It is primarily of two types: according to what is called today the height or pitch (low or high), or according to the duration. One could also speak about order according to the intensity, but this order is not very quantifiable and rather random, since a composer can indicate only in a vague way the intensity of the sounds.
And finally, recognizing preeminence of height over that of the duration, since that one is measured by the frequencies of vibration, Euler brings back the evaluation of the musical pleasure to the arithmetic measurement of the proportions attached to the sounds.
This 'metaphysics' of music is not completely new. The 'result' of Eulerian metaphysics is found already in Antiquity with the Greeks, who had based musical science on the theory of the proportions (cf. the Division of the Canon of the Euclidean school). In the same way, the idea that the music consists of the indirect (or more precisely unconscious) perception of the ratios of the sound frequencies is stated by Leibniz:
"musica est exercitium arithmeticae occultum nescientis se numerare animi."6
But, in spite of these identical themes, the differences should be stressed which mark the originality of Euler. Initially, as one will soon be able to judge, the theory of our mathematician exceeds by far the simple consideration of the ratios of the frequencies of two sounds. Then, contrary to his predecessors, who had also founded their theory on the proportions without any explanation, Euler outlines a philosophical argumentation, in which by the proportions one arrives at the musical pleasure, via the order and the perfection. As for the Leibniz source, one can undoubtedly recognize from it the influence in the distinction which Euler makes between the two modes of perception of the order. But it will be noted that, contrary to the Master of Hannover, he does not venture to speak about unconscious perception; perhaps he does not admit the concept of it, or well, quite simply, he prefers to apply its engineering to develop mathematical calculations rather than philosophical considerations.
That said, let us examine how Euler evaluates the order of the sounds according to their height. By the intermediary of the vibrations of the air, the musical instruments produce regular blows or shocks [ictus] on our tympanum. With a preoccupation for clarity, Euler visualizes these blows, in the case of the simplest chords of two sounds, by the following figures:
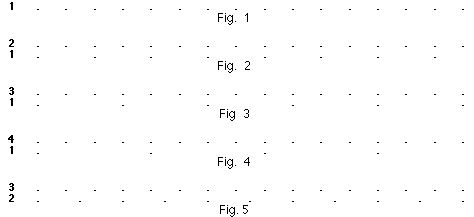
etc...[OO, 3a, I, 231]
This is the place to say some words on the French translation of 1839, since as well the principal topic of our conference [for which Professor Bailhache submitted this paper] is that of the scientific translation. I will be satisfied at a glance on the second chapter, "De suavitate et principiis harmoniae", translated by "On the charms and principles of the harmony". The suavitas will be discussed throughout the work, because one of the major goals that Euler proposes to reach is that to define a scale of "kindness" of the sound aggregates, which he names "suavitatis gradus", "degrees of softness".T4 Useless to notice, under these conditions, that the term of "charm" is not very well selected. Wrote Euler:
"Duobus sonis propositis percipiemus eorum relationem, si intelligamus rationem, quam pulsuum eodem tempore editorum numeri inter se habent; ut si alter eodem tempore 3 pulsus perficiat, dum alter 2, eorum relationem adeoque ordinem cognoscimus observantes hanc ipsam rationem sesquialteram. Similique modo plurium sonorum mutuam relationem comprehendimus, si omnes rationes, quas singulorum sonorum numeri vibrationum eodem tempore editarum inter se tenent, cognoscemus." [OO, 3a, I, 228]
which means [in French]:
"Two sounds being given, we will know the relation which exists between them, if we can grasp the ratio of the number of vibrations carried out for one, with the number of vibrations carried out for the other in the same time. For example, if there were 3 vibrations for the first, while for the second there would be 2 of them, we know their relation and consequently their order, by observing the ratio of the numbers 3 and 2 which is 3:2." [ OCF, 5, 27 ] 7
We see initially that "pulsus" is rendered by "number of vibrations", which corresponds obviously to a desire of modernization of the theory. Literally "pulsus" is an impulse, a shock, and the concept that Euler keeps in mind is certainly that of the shocks (tiny and fast) that the sound bodies produce on the tympanum of the ear by the intermediary of the medium which transmits the sound. In fact, as I explain further on, Euler takes again what one calls now the theory of the coincidence of blows. However, in the following sentence, Euler himself speaks about "numeri vibrationum", which justifies to a certain extent the step of the translator.
We note then that "rationem sesquialteram" is quite simply translated by "3:2". It is again about a modernization, because the sesquialter proportion indicates in Euclid (which Euler takes as a starting point here at least for the terminology) any ratio of the form 1 + 1/n, therefore 3/2 for n = 2.
Let us throw a last glance on the following paragraph:
"Magnum quidem extat in sonorum rationibus percipiendis subsidium, quod singulorum plures ictus percipimus saepiusque eos inter se comparare possumus. Idcirco multo est facilius duorum sonorum rationem discernere audiendo quam duarum linearum eandem rationem habentium intuendo." [OO, 3a, I, 228]
[in French:]
"The appreciation of the relationship between the sounds, is singularly facilitated by this circumstance whereby we perceive several vibrations of each one, and whereby thus we can, for their length of time, compare them several times one with the other. It is thus much easier to distinguish by hearing the ratio of two sounds, than to recognize by the [sense of] sight the same relationship between two lines." [ OCF, 5, 27-28 ]
Again the translation modernizes the term of "ictus" in "vibrations", which however indicates very exactly the "blows" of which I have just spoken.
This rapid examination could lead one to think that the French translation leaves much to be desired. It is certain that it would deserve to be revised to become more precise. However, to judge some by what I know, I believe that one must say all the same that the translator did an intelligent and overall faithful job.
Let us return now to the theory of Euler. The mathematician reasons in the following way.
Then noticing, that 1:5 must be more complex than 1:8 (= 1:23), which has degree 4, Euler allots degree 5 to it and deduces by induction that for a prime number p, 1:p is degree p. Then, this time for p unspecified:
"[...] si ratio 1:p ad gradum, cuius index sit m, referatur, rationem 1:2p ad gradum m + 1 pertinere, 1:4p ad gradum m + 2 et 1:2np ad gradum m + n. Multiplicato enim numero p per 2 ad rationis perceptionem requiritur praeter perceptionem rationis 1:p bisectio aut duplicatio, qua ut simplicissima operatione gradus suavitatis unitate evehitur."
["... if the ratio 1:p to the degree, whose index is m, it is being ascribed, to the ratio 1:2p the degree m + 1 belongs, 1:4p to degree m + 2 and 1:2np to degree m + n. In multiplying a number p by 2 the perception of its ratio requires beyond the perception of the ratio 1:p a bisection or doubling, which is how the simplest operation of one unit of the degree of softness is carried out" - Monzo]
[... if the 1:p ratio belongs to the degree whose index is m, that of 1 with 2p belongs to the degree m + 1, that of 1 with 4p with the degree m + 2, and in general ratio 1 with 2np with the degree m + n; because the multiplication of the number p by 2 gives a ratio only twice as difficult to recognize than the ratio of 1 to p, and increases only one unit the number which expresses the degree of softness of this last. - Bailhache]
And Euler continues by calculating the degree which it is necessary to attach to 1:pq, p and q being again prime:
"Simili modo determinare licet gradum suavitatis rationis 1:pq, si p et q fuerint numeri primi; nam ratio 1:pq eo magis est composita quam 1:p, quo 1:q magis est composita quam 1:1. Ergo rationis 1:pq gradus cum p, q et 1 debet proportionem arithmeticam constituere, unde erit igitur p + q - 1." [OO, 3a, I, 232]
["A similar method is used to determine the degree of softness of ratio 1:pq, if p and q are prime numbers; for ratio 1:pq is more complex than 1:p, while 1:q is more complex than 1:1. Therefore the degree [of softness] of ratio 1:pq with p, q and 1 owes its constitution to the arithmetic proportion, from whence it will be therefore p + q - 1." - Monzo]
[In the same manner one determines the degree of softness of the 1:pq ratio, by supposing that p and q are prime numbers; because between 1:p and 1:pq there is the same difference in composition as between 1:1 and 1:q; consequently the degree of softness of 1:pq must form with degrees 1, p, and q an arithmetical ratio; it will be thus p + q - 1. - Bailhache]
Finally, by observing several times this rule, one can generalize, which produces a formula that Euler does not write, but which amounts to:
the numbers pi being prime and ki being unspecified positive exponents of these numbers.
The cases of more than two sounds are easily reduced to this formula. Thus, four sounds in the 1:p:q:r ratios, with p, q, r prime, will be compared to 1:pqr 8. When the numbers of vibrations are not prime, the procedure is a little more complicated. Let us consider for example the sounds corresponding to 1:pr:qr:ps (p, q, r, s being prime). p and r intervene twice, but being confused by the ear, they should be taken only one time; so that the unit will be compared to 1:pqrs, which is lowest common multiple (LCM) of the factors involved.
Remaining to be considered are the cases where one of the numbers of vibrations is not 1. The fifth 3:2 is an example. One will start then by if required reducing the numbers by dividing them by their highest common factor (HCF) (ex: 4:6:8 give 2:3:4), then, as presently, one will take their LCM. Thus the fifth amounts to the LCM 6 and is thus fourth degree.
We will stop here in this talk for right now, to note several points.
The idea to measure the degree of softness of a chord of two sounds by the scheduling of the blows which one imagines to be the characteristic of a musical sound is not new. Quite to the contrary, it is well accepted so that it is agreed to call it today the theory of the coincidence of blows, i.e., this theory which represented what one could call, within the meaning of Kuhn, the "normal" theory at the time of Galileo and Mersenne. According to this theory, a chord is all the more consonant when the "coinciding" blows resulting from the two sounds are in higher proportion in the whole of the produced blows. But, in truth, in the 1600s, calculations are never taken out to very many places and, what is more, an extremely strange error is systematically made. Instead of taking the proportion in question, one considers that of the blows coinciding compared to the number of blows of the highest sound only. 9
A second remark relates to the step of Euler. It is rather surprising. All is due in fact in the degree of softness p + q - 1 attached to the 1:pq ratio, or, identical in meaning, with two sounds p and q (these numbers being relatively prime). We saw that Euler arrives at this result by a kind of analogical reasoning: the 1:pq ratio "exceeds" 10 1:p as 1:q exceeds 1:1. It is necessary thus that its degree is an arithmetical ratio of p, q and 1, which produces logically p + q - 1. One cannot say that this deduction enjoys a great rigour and carries the conviction, the more so as the former result (the degree p of 1:p) is itself obtained by a synthesis of the same order of probability.
However I say that the result p + q - 1 was directly accessible, in a way much more rigorous. It was enough for that to correctly calculate the degree of softness of the p:q chord in accordance with the theory of the coincidence of the blows. If p and q are two distinct prime numbers (or even relatively prime), it is quite clear that during one period none of their blows will coincide, except those of the beginning and the end of the period. There will be thus one blow coinciding per period (the one period end being the beginning of the following period). And the total number of blows is the sum of all the blows, p +q, decreased by one unit since the two simultaneous blows are perceived like one only (on the example of the 5th, fig. 5 above, one sees there that it has a coincidence and four blows [including this coincidence] per period, which corresponds with 3+2-1). Coincidence being always single, p + q - 1 will be able to constitute an opposite measure of the softness of the chord of the two sounds p and q.11
One can notice as Yves Hellegouarch did 12 that the S(kipi - ki) + 1 is a morphism of the monoid (N, x) in (N, +), which is only one precise manner to indicate the nature of the function. According to an oral comment of Jean Dhombres, it should also be noted that it is the only function which respects the prime numbers (i.e. for p prime, the degree of softness of 1:p is p). But, given the empirical way in which Euler builds this function, it seems extremely improbable that he was perfectly conscious of the unicity of his solution. And Hellegouarch, again, is not wrong to say that "many other functions could be proposed".13
At all events we now have the fundamental elements of the method used by Euler to build his musical theory. The question of consonance of a complex of sounds reduces itself, after division of the components by their HCF, to calculation of degree of softness of their LCM by the formula described above. Euler's Essai is enriched by very many and often very copious tables; the first that he presents to us is thus that of the classification of the LCMs according to the the first sixteen degrees of softness [ OO, 3a, I, 234 ]:
I now will focus my attention on the principal part of Euler's work, namely his mathematical study of harmony, without going however into all the details of the rules of composition with which he graces us, nor to tackle the questions of duration of sounds.
Study of chords of two sounds
The calculation of the LCM attached to each chord, that Euler calls his exponent, provides, by the preceding table, a principle of classification of consonances giving place to a new table ([ OO, 3a, I, 249 ]; I note in boldface characters the ratios which correspond to the fundamental consonances and I underline those which correspond to the traditional dissonances): 14
The classification of the fundamental chords according to Euler is thus:
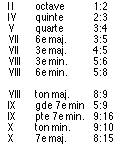
For the consonances, Euler finds thus one of the two classifications that Mersenne had already proposed in the Harmony universelle.15 And as Mersenne had also advanced, Euler affirms that there is no clear border between consonances and dissonances; these last are only "bad" consonances, of a high degree. The table clearly shows it, since it places the two minor consonances (the third and the sixth) at the same degree (VIII) as that of the major tone, which is not absurd from the point of view of perceived reality. We will see what becomes of this idea in the last studies of Euler on music.
Study of the chords of more than two sounds
Up to now there is really nothing new. But the bases of the theory conceal other things well! As one immediately notices it in the table of the chords, to a same "exponent" (the LCM) correspond several groups of possible sounds. Thus, if one considers chords of more than two sounds, the degree of softness will not change when one adds sounds corresponding to dividers of the exponent. 1:2:3:6 is not more "complicated" that 1:6 or 2:3, since all three have 6 for LCM. Consequently Euler defines the concept of a complete chord: a chord will be such if one can add no note to it without its degree becoming any higher, therefore without its exponent not becoming more complex. From this it follows that a chord is complete if it includes all the dividers of its exponent. According to Euler, the ear will then have the impression of plenitude in this degree of chord.16 Here will begin the surprises for somebody who refuses to entirely engage himself with the fruitfulness of the spirit of the great mathematician.
Indeed let us try "to return" to the music of the time of Euler. The first chord which one learns (even still today) is the major triad, the most consonant of all, represented for example by the notes C E G. Not to complicate the situation, let us not add the higher octave to it (C), although that is completely common. These three notes correspond to the three numbers 4, 5, 6, whose LCM is 60. That reveals that it is already of the 9th degree and that the complete chord will be that of the 12 numbers: 1:2:3:4:5:6:10:12:15:20:30:60, i.e. of the twelve notes C1 C2 G2 C3 E3 G3 E4 G4 B4 E5 B5 B6. Here is thus a chord which Euler claims that it will be on the same equal footing of softness as the major triad, a chord which is spread out over six octaves and which in addition to the notes C, E, G, will include also the major 7th B of fundamental C! It will be more complete, certainly, but will it be really more pleasant? Will it be also more practicable? One can doubt it. However, on closer reflection, that is not as absurd as it may seem. Because if one refers to the modern theory of the partial sounds of Helmholtz, it is perfectly exact that in the production of the sounds C, E, G, one also hears the higher partials of the same name, including the B which is the 5th of E and the major 3rd of G. The whole thing is to know the intensities; and, actually, the notes B4 B5 B6 will be very weak.
If one introduces "manually" a C2, the chord C E G C will correspond to numbers 4, 5, 6, 8, of LCM 120. Complexity is then raised one degree, the last note of the complete chord being a B of the seventh octave. This addition of theoretical complexity does not correspond to reality accurately. In fact, to add or not the octave C hardly changes the quality of the chord, with which Euler himself agrees when he analyzes the genera T5 (cf. below).
Study of the successions of chords
This chapter, the fifth of Tentamen, testifies, as if it were necessary, to the originality of Euler in music-theory. No one who had claimed before him "to explain" the consonances by the chord of the blows of the musical sounds had gone further in this way. However music is not only the pure and simple "pictorial" exposure of several harmonies; what is perhaps even more significant, it also consists in a succession, regulated in time, of a series of harmonies.
Euler's idea is simple: it is the same one as for the chords taken separately, i.e. the softness of a succession will depend on the order which it contains. This softness will thus be evaluated by the degree of exponent (the LCM) of the whole complex of sounds from the two successive chords, as if they were emitted at the same time. Two reservations, however, will have to be made.
Initially, as sounds emitted at the same time sound generally harder than if they are followed, one will admit worse degrees (i.e. higher) than in the case of simple consonances.
Then, as it does not act more than one isolated chord, from the point of view of a succession, the possible common factor of the numbers of vibrations of a chord is no longer neglected (i.e., for example, that 2:6:10 are not inevitably any more equivalent to 1:3:5). That complicates things. I prefer to leave the question aside in this rapid survey, 17 restricting myself to saying that the relevance of the interpretation of Euler remains problematic: for example, the resolution of a dominant 7th chord on the triad of tonic is not clearly "explained", since the exponent of the second chord is entirely included in that of the first.18
The genera of Tentamen
Euler gives to his method a universal value. For a succession of more than two chords, for a whole piece of music (!) it is the same principle of evaluation: to calculate the exponent of the whole complex and from it to deduce the degree of softness.
But any piece is played in respect to certain genera. The concept of genus is essential, because the instruments with fixed sounds can produce only one limited number of notes, whose whole will constitute a genus and will correspond to a certain exponent. More exactly, according to Euler, the concept of genus rests on that of octave: a genus is a series of notes which one finds distributed periodically according to several octaves. Here, Euler gives no other justification than that of, a posteriori, design of the existing instruments, 19 which is a defect of his theory which should obviously be as a priori as possible.
This additional principle gives the result that the exponent of a genus will be in the form 2mA, where A will be a product of prime-factors not containing 2, in other words an odd number. But what, more precisely, will A be? Euler answers this question only after having reviewed various genera of the form 2m.3n.5p. He quotes Leibniz who, in a letter to Christian Goldbach, said already:
"Nos in Musica non numeramus ultra quinque, similes illis populis,qui etiam in Arithmetica non ultra ternarium progrediebantur, et in quibus phrasis Germanorum de homine simplice locum haberet: Er kan nicht über drey zählen." 20
["In music we do not go beyond the number 5, similar to those people, who also in arithmetic have not advanced beyond the ternary, and in that German phrase about primitive man of which it is the origin: They cannot count over 3." - Monzo]
Euler develops a genus all the same where the factor 7 intervenes, but by way of pure scholarly hypothesis (one will further see his opinion on this question will change completely in the 1760s):
"Atque sane difficile esset in musicam praeter hos tres numeros alium, puta 7, introducere, cum consonantiae, in quarum exponentes septinarius ingrederetur, nimis dure sonarent harmoniamque turbarent." [OO, 3a, I, 332]
["And it certainly might be difficult in music to introduce beyond these three numbers [2, 3, 5] another, namely 7, since [those] consonances, in which exponents of 7 may be engaged, would sound too harshly and would disturb the harmony." - Monzo]
And it would certainly be difficult to introduce in music another number besides those three, i.e. 7, since the consonances into which the exponent seven is introduced sound too hard and disturb the harmony. - Bailhache]
The combination of powers of 3 and 5 produce 18 genera, of which Euler retained five which have been or still are of use, eliminating four because they are contained in the others and rejecting nine either because they are either too simple, or on the contrary too complicated, i.e. that they give some sound which is too unpleasant, either of the two. The morals of this classification appears clear to me and extremely significant for the theory: the principle even at its foundation (that of the order) is not enough to judge admissibility of a harmony; actually, the historical data play an essential role now, even in the case of the last genus that Euler studies in detail, the genus diatonico-chromaticus, which best approaches the music contemporary with our mathematician.
At this point, it does not seem an exaggeration to say that we "have just made the tour" of the Eulerian theory contained in his work of 1739, a brief tour, certainly. Although extremely abundant, it can be summarized with this: the concept of order is the basis of the principle of taste. This order is measured, as in the old theory, by the coincidence of the blows. However, Euler goes much further than a simple classification of the consonances. He also intends to justify the whole of a series of chords, by measuring its order. But all the definitions, many calculations, the immense tables which our mathematician deploys tirelessly should not make illusion. A certain number of elements foreign to the principle of the order are introduced, all the more "surreptitiously" that, corresponding most of the time to principles admitted by the former theorists, they "pass" without difficulty in front of the eyes of the reader. Thus from there we go particularly to the essential role that Euler makes the number 2 play, i.e. with the octave, to the limitation to only factors 2, 3, 5, and from there to the construction of a finite number of genera, to final restriction on only one genus. In any case, these choices do not really explain the harmonic successions actually used by the musicians. I will quote once again Yves Hellegouarch, who notices pleasantly: "Is this to say also that a musical work remains harmonious when it is played backwards?" Ah yes, indeed, the "principle of the inversion of time", as in traditional mechanics, applies perfectly to the theory of Tentamen. That is to say, that it is far from being adequate!
Beyond Tentamen: evolution of Euler's ideas regarding musical theory
When I first studied Euler's texts on musical theory, it seemed obvious to me that he had never given up his theory, even if he had wanted to supplement it or improve it on certain points until the end of his life. Today I am not as sure of this. Indeed, the reflections which he added to Tentamen, in particular those which relate to the Dominant 7th chord, tend on the contrary to show that it was with the same bases of his first theory that he attacked himself.21
In a paper of 1764, Conjecture about the reason of some dissonances generally received in music, recognizing its practical importance in the contemporary compositions, Euler examines the Dominant 7th chord.22 To the notes G B D F correspond the numbers 36 45 54 64 of exponent (their LCM) 8640 = 26*33*5. Without the "dissonance" F, the exponent of the chord (perfect major) would be equal to 60
"and therefore 144 times smaller than before. From where it seems that the addition of its F spoils too the beautiful harmony of this consonance so that one can grant a place in the music to him. However, with the judgement of the ear, this dissonance is nothing less than unpleasant and one makes use of it in the music with best success; it even seems that the musical composition acquires of it a certain force, without which it would be too plain. Here thus a great paradox, where the theory seems to be in contradiction with the practice, about which I will try to give an explanation. "
Rejecting the explanation of d'Alembert as "too arbitrary and far away from the true principles of harmony"23, Euler starts by recalling, extremely skilfully and pertinently, that the ear tolerates slight variations in the proportions of the consonances (he is not the first to notice it, many others said it before him, but it does not matter here):
"Each time it happens, the perceived proportion is simpler than the real one and the difference is so small that it escapes perception."
Consequently nothing prohibits to suppose that the ear "substitutes" the number 63 for the number 64,
"so that all the numbers becoming divisible by 9, the ratios of our four sounds are now expressed by these numbers 4, 5, 6, 7 whose perception undoubtedly is confounded."
One passes thus to an exponent of 420 instead of 8640 and (what Euler does not specify) two degrees of softness (degree 15 instead of 17) are gained. Euler finds even this astute idea:
"Perhaps this is the foundation of the rule on the preparation and the resolution of dissonances, to inform the listener that it is the same sound, though it can serve as two different ones, so that they he may not imagine that one has introduced a completely foreign sound." [OO, 3a, I, 515]
Here is an original interpretation. One knows indeed that it is usually supposed that preparation and resolution are only used to accustom the ear , beforehand and "subsequently" as one might say, to the dissonant sound by making it hear in consonances. And Euler concludes:
"It is commonly claimed that one makes use in music only of proportions made up of these three prime numbers 2, 3 and 5 and the great Leibniz 24 has already remarked that in music we have still not learned to count beyond 5; which is also incontestably true in the instruments tuned according to principles of the harmony. But, if my conjecture has validity, one can say that in the compositions one already counts up to 7 and that the ear thereby is already accustomed to it. 25 It is a new kind of music, one that has begun to show use and which was unkown to the ancients. In this kind the chord 4, 5, 6, 7 is the most complete harmony, since it contains numbers 2, 3, 5 and 7; but it is more complicated than the common triad which contains only numbers 2, 3 and 5. If it is a perfection in composition, perhaps one will try to carry the instruments to the same degree." [OO, 3a, I, 515]
The theoretical changes are much deeper than it first appears. To start, the dogma of the restriction on only numbers 2, 3, 5 is now abandoned. Then, it would seem that the predilection for the Dominant chord comes from the fact that it is a consonance and not a dissonance. Actually, there is much more. Euler wrote in a paper of 1764, The true character of modern music:
"On this occasion it is significant to notice that the word 'dissonance' is not very specific to express the idea that one attaches to it; this idea is by no means opposed to that which one attaches to the word 'consonance', as the etymology seems to indicate, and therefore, since the consonances are pleasant to the ear, it should not be thought that the dissonances are unpleasant for it, or indeed revolting; with that characterization the dissonances undoubtedly would have to be entirely banished from music. The dissonances thus differ from the consonances in a way that would properly be described as only because they are less simple or more complicated, and it is also necessary that this greater complication is just as pleasant to the ear as the simplicity of the consonances." [OO, 3a, I, 517]
It is no longer exactly by the impression pleasant or unpleasant only that consonances and dissonances are distinguished, but only by their degree of complexity. Thus, at first, Euler had built the mathematical concept of exponent to account for the degree of agreement of the sound combinations. But now, it is the purely intellectual notion of complexity, measured by the exponent, which takes precedence. That same term of degree of softness should now be banished, since a dissonance (the dominant 7th chord) has become pleasant [i.e., more in agreement, in terms of the numbers]. Even the word dissonance is really no longer of use! 26 I believe that in this matter Euler went very far, showed himself very "modern", even if he did not explicitly repudiate the theory of his Tentamen. T1
Furthermore, on this point as on the whole of his theory, one cannot form an opinion of its relevance unless one calls upon more recent explanations, in particular those which are founded on the perception of the beats between the partial sounds [overtones] of the musical notes. These explanations, resulting from the theory of Helmholtz, entirely confirm the principle of the absence of strict segregation between consonances and dissonances. The key is in knowing until which partial sound the ear extends its perception. However that depends on two factors; on the one hand of the relative physical intensity of the partial sounds (the experiment shows that, statistically, 27 it decreases when the order of the partial sound increases), on the other hand of physiological and mental capacity of the listener to perceive the beats according to the height of the simple sounds which produce them. Helmholtz himself will thus take up the idea of the consonance of the Minor 7th as the "natural one" corresponding to ratio 7/4. 28
But the theory of the beats also immediately indicates the limits of the theory of Euler. Because in addition to the fact that it explains why the ear contents itself with approximate ratios, it teaches us that the partials do not have the same importance and that thus the "exponent" of a chord is the only number that characterizes its degree of consonance or of complexity. In particular, to add all the prime factors of the exponent to arrive at what Euler calls a "complete chord" will not improve the chord, as our mathematician imagines it, but will lead rather to the cacophony of a plethora of partial sounds.
1. During the Middle Ages the quadrivium indicated four mathematical "arts": arithmetic, music, geometry and astronomy. This quadrivium constituted the higher part of knowledge, in opposition to trivium, the elementary part, which comprised grammar, rhetoric and dialectic. (back to text)
2. Cf. our work Leibniz et la théorie de la musique
[Leibniz and the theory of music], Klincksieck, coll. "Domaine musicologique", 1992, 158 p.
(back to text)
3. [OO, 3a, I, x-xiv]. This reference, like the following ones
of Euler, refers to
Opera Omnia,
series tertia, volumen primum, "Opera physica, miscellanea,
epistolae"; Lipsiae et Berolini, 1926.
(back to text) 4. the majority in French.
(back to text) 5. I will leave aside the pages devoted to
music theory
in the Letters to a German princess (hardly sixteen pages
out of nearly six hundred). They contain only one kind of ultra-simplified
extract of Tentamen.
(back to text) 6. "Music is an occult practice of arithmetic in which the spirit
is unaware that it counts." (letter to Chr. Goldbach of
17 April 1712). Cf. our book, already quoted,
Leibniz et la théorie de la musique, p. 151.
(back to text) 7. As above for [OO], we indicate by
[OCF] the references to
OEuvres Complètes en Français
de L. Euler [Complete Works in French of L Euler]
, edited by l'Association des capitaux intellectuels pour favoriser le
développement des Sciences physiques et mathématiques
[Association
of the intellectual capitals to support the development of the
Physical and mathematical sciences],
volume 5, which contains the Essai sur la
musique [Essay on music] and
three other papers on the same subject.
(back to text) 8. The prime numbers resulting from two different sounds must be
distinct. If not,
1:p:p
will be compared to 1:p and not to
1:p2, because the
two sounds p are
taken by the ear as a single sound.
(back to text) 9. Cf. for example our study "Cordes
vibrantes et consonances chez Beeckman, Mersenne et Galilée",
[vibrating Cords and consonances in Beeckman, Mersenne and Galileo]
Sciences et techniques en
perspective, 23, especially $3,
p. 81 - 88. This error is made
by Galileo without any ambiguity:
"Thus the first and the most pleasant consonance will be that
of the octave, since to each percussion of the tympanum due to
the lowest string correspond two percussions caused by the
highest string: with the time of one vibration on two of the highest string
the effects will thus come to be combined, so that half of the
percussions on the whole will beat the ear together; on their
side two strings in unison, vibrating always together, give the
impression of only one string and for this reason do not produce
any consonance. The 5th also is pleasant, by the fact that
to two pulsations of the lowest string corresponds each time
three pulsations of the highest string: if thus one counts according
to the vibrations of the latter, a third of all the vibrations takes
place together, which means that two solitary vibrations come to be
intercalated between each couple of concordant vibrations;
in the 4th, these are three solitary vibrations which will come
to be intercalated."(Discours et
démonstrations mathématiques concernant deux sciences
nouvelles [Discourse and mathematical demonstrations
concerning two new sciences], trans. Clavelin, A. Colin, Paris
1970, p. 85. Emphasis Bailhache's.)
(back to text)
10. "magis est composita" = exceeds in complexity. (back to text)
11. Or, if one prefers, 1/(p + q - 1) will be able to constitute a direct measure of this softness. It is this value which Galileo, Mersenne and their contemporaries "should" have found. (back to text)
12. Yves Hellegouarch, "L'"Essai d'une nouvelle théorie de la musique" de Leonhard Euler" [The 'Essay on a new theory of music' of Leonhard Euler], publication of l'IREM de Caen, 19??, p. 53. (back to text)
13. Ibid. (back to text)
14. Euler presents these ratios in the opposite order of that which is usual today (1:2 instead of 2:1, etc). One could believe it an archaism, since the Greeks proceeded in this manner. But Euler simply seeks to place the numbers in an ascending order. (back to text)
15. Cf. our article, already quoted, "Cordes vibrantes et consonances chez Beeckman, Mersenne et Galilée", p. 82. (back to text)
16. Consequently:
If the exponent is prime, the complete chord will be composed of two notes: 1:a.
If the exponent is am (a prime), the complete chord will be composed of (m + 1) notes: 1:a:a2:...:am.
If the exponent is ab (a et b prime), the complete chord will have 4 notes: 1:a:b:ab.
etc...If the exponent is am bn cp (a, b, c prime), the complete chord will be composed of (m+1)(n+1)(p+1) notes (this is the well-known rule on the number of divisors of a entirety broken up into products of prime-factors).
Euler accompanies his definition by an immense table of the complete chords of the first 12 degrees. (back to text)
17. Cf. My former studies: "Deux mathématiciens musiciens [Two mathematican-musicians]: Euler et d'Alembert", Physis, Rivista internazionale di storia della scienza, vol. XXXII, Nuova Serie, Fasc. 1, 1995, p. 1-35 (communication in 19th International Congress of History of sciences, Saragossa, August 22-29, 1993); "Sciences et musique: quelques grandes étapes en théorie musicale [Sciences and music: some great stages in musical theory]", to appear in Littérature, Médecine, Société, 13, Université de Nantes. (back to text)
18. See my comments in the texts quoted with the preceding note. (back to text)
19. [OO, 3a, I, 290], $5 et 6. (back to text)
20. The reference (without quotation specifics) is made in the Tentamen page 332, by way of citing authority. Later, in an article of 1764, Euler produces the quotation supplements [OO, 3a, I, 515], but this time to protest against the principle which it claims to pose. (back to text)
21. Also, in 1773, the Euler's ideas as regards physics of the musical sound became perfectly "modern":
"Incipiamus igitur ab unisono, qui constat perfecta aequalitate duorum pluriumve sonorum musicorum; cum enim omnis sonitus motu vibratorio sive tremore in aere excitato producatur, sive iste tremor fuerit aequabilis sive inaequabilis, in musica alii sorti non admittuntur, nisi ubi omnes vibrationes inter se sunt isochronae sive aequalibus tempusculis absolvuntur." [OO, 3a, I, 569, "De harmoniae veris principiis per speculum musicum repraesentatis"].Now, it is no longer a question of ictus or of pulsus and the translator can correctly say:
"Let us start with the unison, which consists in the perfect equality of two or several sounds of music. Any sound owes its birth to a vibratory movement produced in the air, the vibrations being equal or unequal between them; but in music one admits as other sounds only those which are due to isochronous vibrations, i.e. to vibrations carried out in equal times." [OCF, 5, 253](back to text)
22. Cf. [OO, 3a, I, 509 ff.] Euler considers also his first inversion, of which it is useless to speak here. (back to text)
23. [OO, 3a, I, 510]. (back to text)
24. Euler produces here the quotation which we reported above. (back to text)
25. In another article, Euler says still better: "we will be able to say with the late Mr. Leibniz that music now learned how to count up to seven." [OO, 3a, I, 525] (back to text)
26. "Musicians agree that certain chords [such as the Dominant 7th] could not be reconciled with the principles of harmony and they try to support them by the name of dissonance that they impose on them; but, if they understand by this term a chord where the ear could not discover any ratio, one should be able to to use it with as much success as all other mixture of tone, absurd as it is; the musicians are quite unwilling to admit that." [OO, 3a, I, 524] (back to text)
27. I.e. on average according to the various instruments. Only instruments of very distinctive timbre, like the clarinet, present partial sounds of intensity higher than the tenth. (back to text)
28. Cf. Helmholtz, Théorie physiologique de la musique, fondée sur l'étude des sensations auditives, [French] trans. G. Guéroult, Paris, 1874 [Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, 1863], p. 249, 293 and 441 for the references to the chord of ratio 7/4. However, Helmholtz finally rejects this chord, like others founded on number 7, for the reason that its inversion is "worse than itself". And he concludes that "there is thus a true gap in the series of the intervals arranged according to their harmony, and it is this gap which forms the limit between the consonances and the dissonances." (p. 293).
[English translation of Helmholtz by Alexander Ellis, On the sensations of tone as a physiological basis for the theory of music, 1875. Dover Reprint 1954 based on 2nd edition of Ellis. In this edition, Helmholtz discusses the ratio 7/4 on p 195, and a chord relating to it on p 344. I do not have the French edition available for correlation. feedback welcome] (back to text)
T2.
I think it is important to translate
'causa horologium'
as 'clockwork' rather than just
'clock',
with an emphasis on the mechanism,
especially since in today's digital age
'clock' does not
give the same picture in the reader's mind as it would have
in Euler's day.
Euler's main reason for choosing a clock as his example
was that in his day it was the most complicated mechanism
encountered by most people in ordinary daily life.
His whole point here is to show how the order in this intricate
mechanism is what results in the perfection of its actions.
I think it is quite an ingenious example, not just because of
this obvious characteristic,
but also because of the other connotations associated with the clock:
the most elusive aspect of music
is its prolongation thru time, and time plays a major
role in the analysis of
frequency ratios, which will turn out
to be the ultimate subject of Euler's paper.
This reference to a clockwork strengthens my belief that
in his mind Euler had a latent model of these rational relationships
as a harmonic lattice diagram,
and thus makes his work a significant precursor to my own.
(back to text) T1.
This is exactly the position taken by such later theorists as
Schoenberg (Harmonielehre, 1911), Partch (Genesis of a Music,
1947, 1974) and myself (JustMusic, 1995).
See the dictionary entrance for
sonance.
(back to text) T4.
Prof. Bailhache prefers to translate
'suavitas' into English by the term
'softness',
so I have done so thruout.
However, the term can
be translated by a variety of English words which are not
necessarily synonymous. Some examples are
'sweetness',
'agreeableness', and
'agreement'.
Among the most successful, in my opinion, are
'attractivness',
and one which has a duality of meaning that may (or may not)
have been intended by Euler,
'attraction'.
(back to text) T5.
Although ordinarily the English translation for the French
genres
would be scales, the term
Euler Genus is already in common use
in English to refer to the particular types of scales under discussion.
(back to text) T6.
John Chalmers sent me the following:
To the best of my knowledge, Euler never constructed any genera using 7
and Fokker was the first to do so. Correct?
Who first discovered that sounds are not trains of pulses (as the
ancients thought), but sine waves? Who discovered overtones, Mersenne?
Professor Bailhache has contributed:
BIBLIOGRAPHY on Euler
University of St. Andrews (Scotland)
Euler, Leonhard.
English translation by Charles Samuel Smith,
Rameau, Jean-Philippe
[The text translated here]
Not Mersenne alone! It is a complicated story!
Biography of Euler webpage
1739 Tentamen novae theoriae musicae. Sint Petersburg.
In Opera Omnia series III volumen I,
Teubner, Leipzig, 1926.
PhD diss., Indiana University,
Bloomington, June 1960.
1760 Exposition de quelques nouvelles vues mathématiques
dans la théorie de la musique.
Amsterdam.
1764 "Conjecture de la raison de quelques dissonances
généralement reçues dans la musique",
Mémoires de l'Academie Royale de Berlin, vol. 20, 1764.
1764
"Tentamen de sono campanarum".
Novi commentarii Academiae Scientiarum
Imperialis Petropolitanae, tom. 10, 1764.
1774 De harmoniae veris principiis perspeculum musicum
repraesentatis.
Brun, Viggo
1753 Extrait d'une réponse de M. Rameau àM. Euler sur l'identité des octaves. Paris.
Vogel, Martin
1959 "Mehrdimensionale Algorithmen, welche die Eulersche Kettenbruchentwicklung der Zahle verallgemeinern", Festschrift Leonard Euler zum 250. Geburtstag, Akademie-Verlag, Berlin.
Busch, Hermann R
1960 "Die Musikschriften Leonhard Euler", in the preface to Euleri opera omnia, series III, vols. 11-12, Zürich.
Lindley, Mark
1970 Leonhard Eulers Beitrag zur Musiktheorie. Kölner Beiträge zur Musikforschung vol. 58, Gustav Bosse Verlag, Regensburg.
Klösch, Gerhard
1981 "Leonhard Euler als Musiktheoretiker", in Kongreßbericht Bayreuth 1981, Kassel.
Craats, Jan van de
1988 "Von der Eulerschen Konsonanztheorie zum relationalen Tonsystem. Ordnung in der Unendlichkeit der Töne", Mikrotöne II, Edition Helbling, Innsbruck, pp. 51-64.
Muzzulini, Daniel
1989 De Fis van Euler. Aramith Uitgevers, Bloemendaal, 144 pages.
Bailhache, Patrice
1994 "Leonhard Eulers Konsonanztheorie", Musiktheorie vol. 9 no. 2, 1994. Laaber Verlag, Laaber, Germany.
Hellegouarch, Yves
1997 "La Musique traduite en Mathématiques: Leonhard Euler", Communication au colloque du Centre François Viète, "Problèmes de traduction au XVIIIe siècle", Nantes, 17 janvier.
no date "L'Essai d'une nouvelle théorie de la musique de Leonhard Euler", publication de l'IREM de Caen, p. 53.
I would like to thank the author for his generous assistance
in helping me with the Latin translations.