prime-mapping
For a regular temperament of rank n, or in other words of "dimension" n-1, the prime mapping is a list of n vals which defines how the prime intervals are to be expressed in terms of the particular set of generators chosen.
For instance, [<1 2 4 7|, <0 -1 -4 -10|] is a prime mapping for 7-limit meantone; in terms of the two generators P and G -- notated here as [<P|, <G|] --, it says (expressed additively) that:
| prime | map |
| 2 | P |
| 3 | 2P - G |
| 5 | 4P - 4G |
| 7 | 7P - 10G |
so the generators are an octave and a fourth.
We could equally well express meantone in terms of 12P+7G and 19P+8G, in which case the prime mapping would be given by [<12 19 28 34|, <19 30 44 53|]. Either system could be useful; using the second one any meantone tuning between 12 and 19 is expressed as a linear combination using non-negative integer coefficients of the 12 and 19 vals.
It is often useful to work on prime-mappings as matrices. Gene's example mapping above would be notated thus:
P = < 1 2 4 7 | G = < 0 -1 -4 -10 |
See Gene Ward Smith's definition of "regular temperament", for which i provide an illustration below.
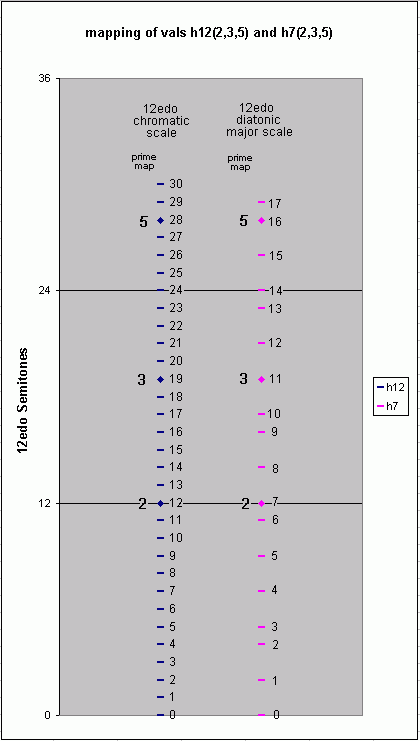
For example, the familiar 12-edo tuning, -- considered as both the 12-tone chromatic scale and the 7-tone diatonic major scale -- maps the "2-tuple of vals [h12, h7], where h12 = [12, 19, 28] and h7 = [7, 11, 16]" shown in Gene Ward Smith's example linked to above as follows, in the 5-limit:
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
