tritone
A musical interval composed of three successive 'whole tones', which is what the word "tritone" literally means. This interval is technically the "augmented 4th", but the word "tritone" is also used generally to refer to its complement, the diminished 5th.
The tritone in the 12-tone equal tempered scale divides the 'octave' precisely in half, and thus has a size of exactly 600 cents or 6.00 Semitones. Mathematically, since the "octave" is the ratio 2:1, this tritone is the square-root of 2, also written 2(1/2).
Any equal-temperament with an even number of degrees has this 'perfect tritone'.
Scales tuned to just intonation, meantone, and other tuning systems based on just intonation tend to have two different-sized 'tritones' which fall on either side of this exact division.
The tritone, as both "augmented 4th" and "diminished 5th", originally arose in pythagorean tuning. In this system, the "whole-tone" has the ratio 9:8. Three of them are mathematically (9/8)3 = ratio 729/512, expressed in decimal form as exactly 1.423828125, with a logarithmic interval size of ~611.7300052 cents, which is the augmented 4th:
note F G A B
ratio (C=n0) 4/3 3/2 27/16 243/128
prime-factor 3-1 31 33 35
ratio (F=n0) 1/1 9/8 81/64 729/512
prime-factor n0 32 34 36
~cents 0 204 408 612
\/ \/ \/
9/8 9/8 9/8
32 32 32
204 204 204
tone tone tone
The diminished 5th is the result of ascending two tones and two diatonic semitones. In pythagorean tuning this is mathematically (9/8)2(256/243)2 = ratio 1024/729, expressed in decimal form as exactly 1.404663923182441700960219478737997256515775034293552812071330589849108367626886145... (the decimal part repeats after the 81st place), with a logarithmic interval size of 5.88 Semitones = ~588.269994807675 cents:
note B C D E F
ratio (C=n0) 243/128 1/1 9/8 81/64 4/3
prime-factor 35 n0 32 34 3-1
ratio (B=n0) 1/1 256/243 32/27 4/3 1024/729
prime-factor n0 3-5 3-3 3-1 3-6
~cents 0 90 294 498 588
\/ \/ \/ \/
256/243 9/8 9/8 256/243
3-5 32 32 3-5
90 204 204 90
semitone tone tone semitone
The "standard" 5-limit just intonation tritone (augmented-4th) is the ratio 45:32, expressed in decimal form as exactly 1.40625, with a logarithmic interval size of 5.90 Semitones = ~590.22371559561 cents:
note F G A B
ratio (C=n0) 4/3 3/2 5/3 15/8
prime-factor 3-1 31 3-151 3151
ratio (F=n0) 1/1 9/8 5/4 45/32
prime-factor n0 32 51 3251
~cents 0 204 386 590
\/ \/ \/
9/8 10/9 9/8
32 3-251 32
204 182 204
tone tone tone
Also frequently encountered is its complement 64:45 (=~ 610 cents):
note B C D E F
ratio (C=n0) 15/8 1/1 9/8 5/4 4/3
prime-factor 3151 n0 32 51 3-1
ratio (B=n0) 1/1 16/15 6/5 4/3 64/45
prime-factor n0 3-15-1 315-1 3-1 3-25-1
~cents 0 112 316 498 610
\/ \/ \/ \/
16/15 9/8 10/9 16/15
3-5 32 32 3-5
112 204 182 112
semitone tone tone semitone
Typical 7-limit tritones are 7:5 (= ~583 cents) and its complement 10:7 (= ~617 cents), whose fractions have much smaller integer terms than the 3- and 5-limit tritones.
Below is a table of many 13-limit ratios which may represent the tritone. These are all the tritones (i.e., between 580 and 620 cents) which are elements of the set of just intonation pitch-classes bounded by 3(-10...10) * 5(-2...2) * 7(-1...1) * 11(-1...1) * 13(-1...1). Interval names are from Manuel Op de Coul's Scala file "intnam.par".
prime-factor 2 3 5 7 11 13 ratio numerator denominator cents interval name 9 -9 1 0 1 0 1.430676218 28160 / 19683 620.0366484 25 -8 -2 0 -1 -1 1.430552523 33554432 / 23455575 619.8869612 -3 -7 2 1 1 1 1.430326932 25025 / 17496 619.6139323 13 -6 -1 1 -1 0 1.430203267 57344 / 40095 619.464245 -14 8 2 -1 0 0 1.430184501 164025 / 114688 619.4415282 -2 0 -2 0 1 1 1.43 143 / 100 619.2181764 1 0 1 -1 0 0 1.428571429 10 / 7 617.4878074 Euler's tritone -11 2 2 0 0 1 1.428222656 2925 / 2048 617.0650912 -10 9 -2 -1 0 1 1.427896205 255879 / 179200 616.6693354 -4 3 0 0 1 -1 1.427884615 297 / 208 616.6552832 -16 5 1 1 1 0 1.427536011 93555 / 65536 616.232567 0 6 -2 1 -1 -1 1.427412587 5103 / 3575 616.0828798 16 -8 0 -1 0 0 1.426960176 65536 / 45927 615.5340866 4 -6 1 0 0 1 1.426611797 1040 / 729 615.1113704 11 -5 -1 0 1 -1 1.426274137 22528 / 15795 614.7015624 -1 -3 0 1 1 0 1.425925926 77 / 54 614.2788462 -4 3 1 -1 -1 1 1.424512987 1755 / 1232 612.5625294 3 4 -1 -1 0 -1 1.424175824 648 / 455 612.1527214 -9 6 0 0 0 0 1.423828125 729 / 512 611.7300052 Pythagorean tritone -21 8 1 1 0 1 1.423480511 2985255 / 2097152 611.307289 -14 9 -1 1 1 -1 1.423143592 1515591 / 1064960 610.897481 11 -5 0 -1 -1 1 1.422906312 26624 / 18711 610.6088086 18 -4 -2 -1 0 -1 1.422569529 262144 / 184275 610.1990006 6 -2 -1 0 0 0 1.422222222 64 / 45 609.7762844 2nd tritone -6 0 0 1 0 1 1.421875 91 / 64 609.3535682 1 1 -2 1 1 -1 1.42153842 462 / 325 608.9437602 9 -2 2 -1 -1 -1 1.42080142 12800 / 9009 608.0459154 21 -10 -2 0 0 0 1.420618131 2097152 / 1476225 607.8225636 9 -8 -1 1 0 1 1.4202713 46592 / 32805 607.3998475 -18 6 2 -1 1 1 1.42025266 2606175 / 1835008 607.3771306 -2 7 -1 -1 -1 0 1.42012987 2187 / 1540 607.2274434 -14 9 0 0 -1 1 1.419783159 255879 / 180224 606.8047272 -8 3 2 1 0 -1 1.419771635 4725 / 3328 606.790675 -7 10 -2 0 0 -1 1.419447115 59049 / 41600 606.3949192 24 -10 1 -1 -1 -1 1.419198932 83886080 / 59108049 606.0921946 12 -8 2 0 -1 0 1.418852448 102400 / 72171 605.6694784 -3 -2 1 -1 1 1 1.418650794 715 / 504 605.4234098 13 -1 -2 -1 -1 0 1.418528139 8192 / 5775 605.2737226 1 1 -1 0 -1 1 1.418181818 78 / 55 604.8510064 7 -5 1 1 0 -1 1.418170307 4480 / 3159 604.8369542 -4 4 -2 1 0 0 1.4175 567 / 400 604.0184822 12 -10 0 -1 1 1 1.41705073 585728 / 413343 603.469689 16 -7 -2 0 -1 1 1.416582284 851968 / 601425 602.8972856 -1 4 1 0 -1 -1 1.416083916 405 / 286 602.2881132 -16 10 0 -1 1 0 1.415882656 649539 / 458752 602.0420445 -13 6 2 1 -1 0 1.415738192 127575 / 90112 601.865397 10 -7 2 -1 1 -1 1.414954501 281600 / 199017 600.9067958 14 -4 0 0 -1 -1 1.414486748 16384 / 11583 600.3343924 -1 2 -1 -1 1 0 1.414285714 99 / 70 600.0883238 2nd quasi-equal tritone 2 -2 1 1 -1 0 1.414141414 140 / 99 599.9116762 quasi-equal tritone -13 4 0 0 1 1 1.41394043 11583 / 8192 599.6656076 -9 7 -2 1 -1 1 1.413473011 199017 / 140800 599.0932042 14 -6 -2 -1 1 0 1.412690574 180224 / 127575 598.134603 17 -10 0 1 -1 0 1.412546437 917504 / 649539 597.9579555 2 -4 -1 0 1 1 1.412345679 572 / 405 597.7118868 -15 7 2 0 1 -1 1.411848802 601425 / 425984 597.1027144 -11 10 0 1 -1 -1 1.411382075 413343 / 292864 596.530311 5 -4 2 -1 0 0 1.410934744 800 / 567 595.9815178 -6 5 -1 -1 0 1 1.410267857 3159 / 2240 595.1630458 0 -1 1 0 1 -1 1.41025641 55 / 39 595.1489936 -12 1 2 1 1 0 1.409912109 5775 / 4096 594.7262774 4 2 -1 1 -1 -1 1.40979021 1008 / 715 594.5765902 -11 8 -2 0 1 0 1.409589844 72171 / 51200 594.3305216 -23 10 -1 1 1 1 1.409245706 59108049 / 41943040 593.9078054 8 -10 2 0 0 1 1.408999306 83200 / 59049 593.6050808 9 -3 -2 -1 0 1 1.408677249 6656 / 4725 593.209325 15 -9 0 0 1 -1 1.408665815 360448 / 255879 593.1952728 3 -7 1 1 1 0 1.40832190 3080 / 2187 592.7725566 19 -6 -2 1 -1 -1 1.40820014 3670016 / 2606175 592.6228694 -8 8 1 -1 0 -1 1.408181662 32805 / 23296 592.6001525 -20 10 2 0 0 0 1.407837868 1476225 / 1048576 592.1774364 -8 2 -2 1 1 1 1.40765625 9009 / 6400 591.9540846 0 -1 2 -1 -1 1 1.406926407 325 / 231 591.0562398 7 0 0 -1 0 -1 1.406593407 128 / 91 590.6464318 -5 2 1 0 0 0 1.40625 45 / 32 590.2237156 tritone -17 4 2 1 0 1 1.40590677 184275 / 131072 589.8009994 -10 5 0 1 1 -1 1.40557398 18711 / 13312 589.3911914 15 -9 1 -1 -1 1 1.40533956 2129920 / 1515591 589.102519 22 -8 -1 -1 0 -1 1.405006942 4194304 / 2985255 588.692711 10 -6 0 0 0 0 1.404663923 1024 / 729 588.2699948 Pythagorean diminished fifth -2 -4 1 1 0 1 1.404320988 455 / 324 587.8472786 5 -3 -1 1 1 -1 1.403988604 2464 / 1755 587.4374706 2 3 0 -1 -1 0 1.402597403 108 / 77 585.7211538 -10 5 1 0 -1 1 1.402254972 15795 / 11264 585.2984376 -3 6 -1 0 0 -1 1.401923077 729 / 520 584.8886296 -15 8 0 1 0 0 1.401580811 45927 / 32768 584.4659134 1 -6 2 -1 1 1 1.401136586 7150 / 5103 583.9171202 17 -5 -1 -1 -1 0 1.401015445 131072 / 93555 583.767433 5 -3 0 0 -1 1 1.400673401 416 / 297 583.3447168 11 -9 2 1 0 -1 1.400662032 358400 / 255879 583.3306646 12 -2 -2 0 0 -1 1.40034188 4096 / 2925 582.9349088 0 0 -1 1 0 0 1.4 7 / 5 582.5121926 septimal or Huygens' tritone, BP fourth 3 0 2 0 -1 -1 1.39860139 200 / 143 580.7818236 15 -8 -2 1 0 0 1.39842097 229376 / 164025 580.5584718 -12 6 1 -1 1 0 1.398402623 40095 / 28672 580.535755 4 7 -2 -1 -1 -1 1.398281718 34992 / 25025 580.3860677 -24 8 2 0 1 1 1.398061216 23455575 / 16777216 580.1130388 -8 9 -1 0 -1 0 1.397940341 19683 / 14080 579.9633
Below is a graph of these tritones's cents values.
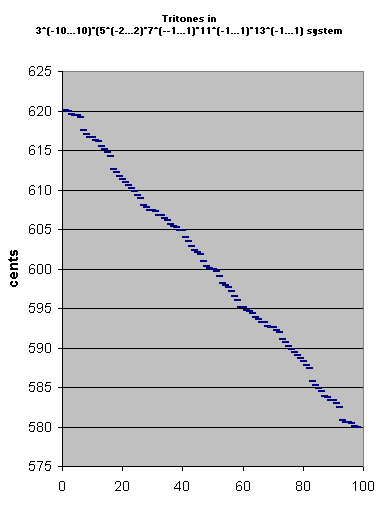
24:17 (= ~597 cents) and 17:12 (= ~603 cents) are two 17-limit tritones.
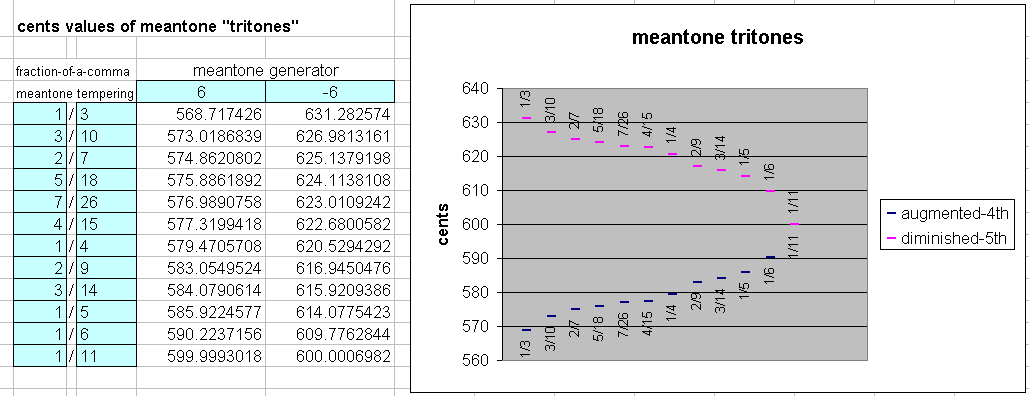
Below is a table and graph of the tritones for some of the most common fraction-of-a-comma meantones. They show both the "augmented 4th" (+6 generator) and "diminished 5th" (-6 generator) for each meantone. The numerator and denominator of the fraction-of-a-comma tempering of each "5th" (generator) is shown in blue on the left. Values are given in cents.
Note that for all intents and purposes, 1/11-comma meantone is identical to the standard 12-edo scale, and that 1/3-comma is nearly identical to 19-edo, 3/10-comma is essentially the same as LucyTuning, both 4/15-comma and 7/26-comma can represent golden meantone, 1/4-comma resembles 31-edo, and 1/6-comma resembles 55-edo.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
