> From: Paul Erlich
> To: tuning@yahoogroups.com
> Sent: Monday, December 03, 2001 2:49 PM
> Subject: [tuning] Re: Re : The C-Fb-G major triad: Pythag-Just tuning.2
>
>
> Pythagorean tuning is clearly based on a chain of fifths. The Arabic
> theorists simply lengthened this chain, perhaps to justify scales
> already in use that didn't fit the Greek mold. There is
> circumstantial evidence that they stumbled upon the schisma (much as
> the West did later, around 1420), since they used it to construct,
> essentially, 5-limit just scales.
(Those who have trouble following the Greek terminology here may get some help from my "Tutorial on ancient Greek Tetrachord-theory".
In my unpublished paper "An Examination of a Possible 5-Limit System of Boethius" (1997), the conclusion of which appears in my book JustMusic: A New Harmony, I examine the Greek-letter notation used by Boethius to describe the modes.
There, I assume that the ratios described by Didymus are used for the diatonic genus, and construct a lattice incorporating all of the pitches which occur in the complete set of all the modes.
I note how pitches which are separated by a syntonic-comma always have different symbols, but those separated by a skhisma always have the same symbols.
Boethius's actual theoretical tuning of the diatonic genus supposedly would have been entirely Pythagorean (3-limit), but as Nicomachus wrote, c. 100 AD:
>> [Barker 1989, p. 265]
>>
>> ... [the synemmenon tetrachord] begins with its own trite
>> a semitone away from mese, then, after a tone, has a paranete
>> peculiar to itself, then, after another tone, has the nete synemmene,
>> which is in all respects of the same tension and sound
>> as paranete diezeugmenon.
And this distinction is indicated in Boethius's Greek-letter notation.
Much later (c. 900 AD), Hucbald directly contradicted this:
>> [Babb 1978, p 33]
>>
>> ... the paranete synemmenon is the same in sound as trite diezeugmenon.
which shows that the basic diatonic tuning had changed by his time.
The only tuning system which would have been a good candidate for Boethius's time which gives pitches matching his descriptions and notations, is that of Didymus (c. 50 BC - 100 AD), where the protypical tetrachord is [descending]:
mese A n^0 1:1
> -9:8
lichanos meson G 3^-2 16:9
> -10:9
parhypate meson F 5^-1 8:5
>> -16:15
hypate meson E 3^1 3:2
Boethius's description and diagrams of the modal system are in his Book 4, chapters 16 and 17 [Bower 1989, p 154-160]. A link to the Latin text is given below.
Constructing lattices for each mode notated by Boethius, but according to the tuning of Didymus, results in a general lattice for the whole system, with pairs of pitches which are separated by a skhisma (~2 cents) but notated with the same letter, one of them occuring with the pair 3^3 (= 27:16 = ~906 cents) and 3^-5 * 5^-1 (= ~904 cents), and another with the pair 3^2 (= 9:8 = ~204 cents) and 3^-6 * 5^-1 (= ~202 cents).
There are several pairs of pitches separated by a syntonic-comma (= ~21.5 cents), and in every case the two notes have different symbols representing them.
A pitch-height and monzo analysis of one mode of the entire Perfect Immutable System, in the diatonic genus, is given in the graph below.
Shown left to right are: the tetrachord name and extent, then the note name; then, a plot of the note's pitch-height, and the note's cents-value, and 2,3,5-monzo, all relative to the 1/1 mese, which is at the vertical center.
Note the synemmenon tetrachord's "paranete peculiar to itself" (294 cents, compared to ~316 cents for the trite diezeugmenon), as described by Nicomachus.
Below is a lattice of the system in 2,3,5-prime-space. Each monzo in the graph above determines the location of the pitch's cube in the lattice; the cubes are labeled with cents-values. The x,y,z axes represent respectively the prime-factors 2, 3, and 5.
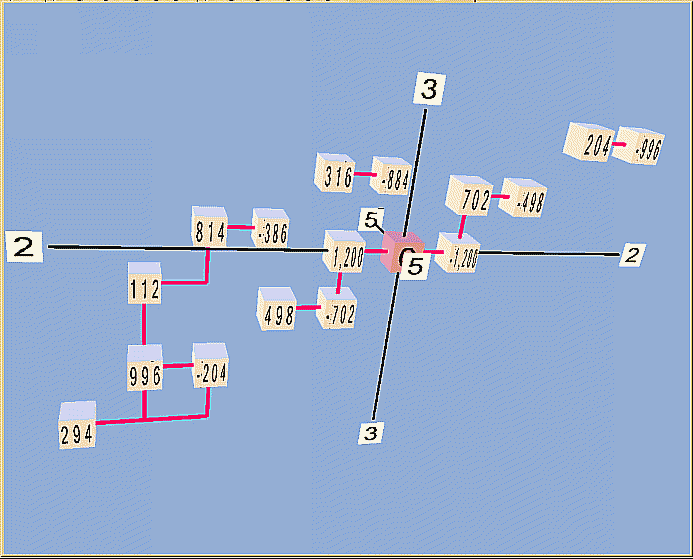
Below are three views of a lattice in 2-3-5-space of the entire modal-system gamut shown in Boethius's diagrams. Here, the x,y,z axes represent respectively the generators 3/2, 5/4, and 2/1.
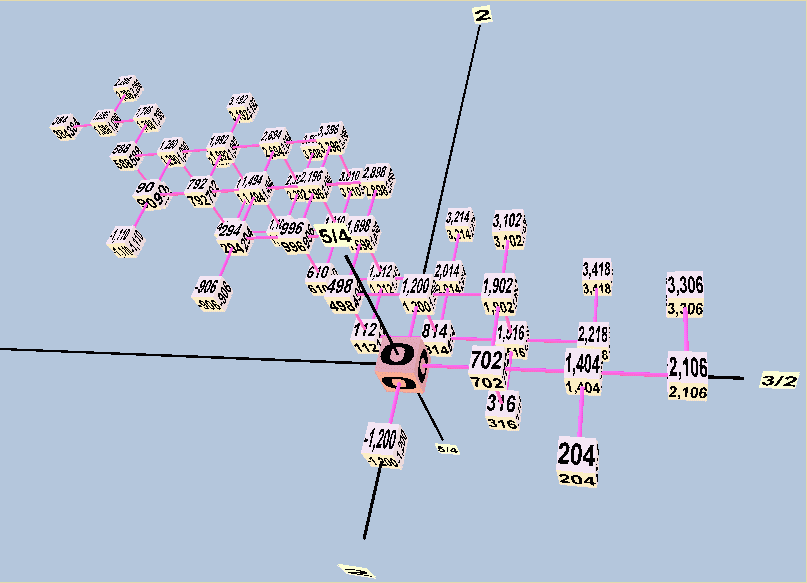
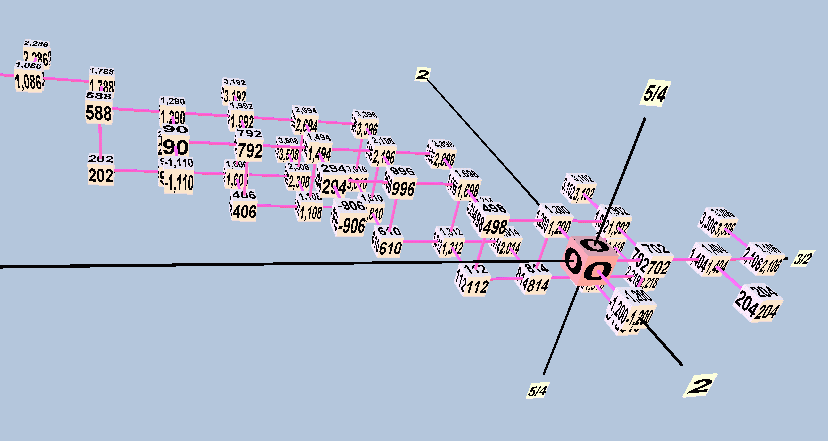
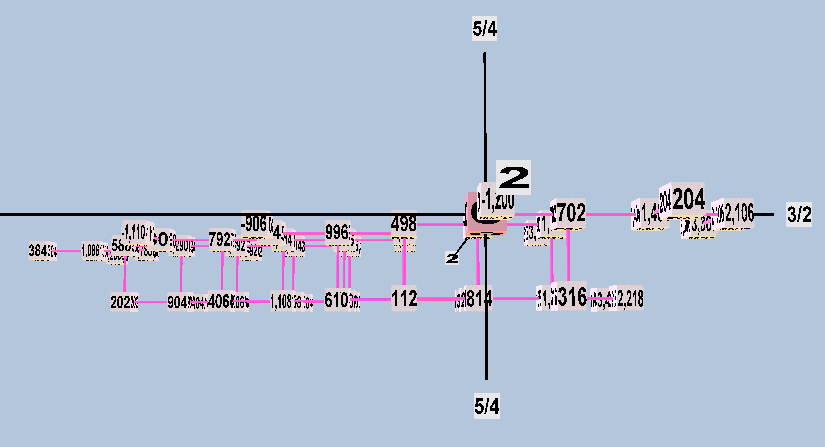
Taken together, and assuming that the tuning of Didymus is correct, I believe the evidence of the Greek-letter notation indicates that musicians of the late classical and early post-classical period (c. 100 BC - 500 AD):
If I'm correct that ancient Greek musicians *in practice* (i.e., in their actual musical notation) recognized the skhisma, then it's no surprise at all that later Arab music-theorists picked it up, as they did so many other ancient Greek concepts.
Here, the skhisma has been designated as a unison-vector -- thus, the notes interpreted by Monzo can ignore skhisma differences, and can be viewed as a 19-tone chain-of-5ths from 3^-8 ... 3^10, i.e., if A is the reference, the chain extends from Db to Fx.
REFERENCES
Barker, Andrew (ed.). 1989.
Bower, Calvin M. (ed., trans.). 1989.
Boethius, Anicius Manlius Severinus. c. 505.
Hucbald of St. Amand. c. 880.
Joe Monzo & Ozan Yarman. 2005.
Warren Babb (trans.). 1978.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.